?

About 23 minutes to nine.
Use the big hand for the minutes and the smaller had for the hours.

Peak Warming Man said:

About 23 minutes to nine.
Use the big hand for the minutes and the smaller had for the hours.

You blokes crack me up.

and holy shit, I’ve just realised that cb88 must have added some code and I can easily paste from Mathcad. WhooHoo!@!!

2 looks like the equation

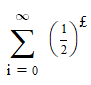
sibeen said:

2 looks like the equation

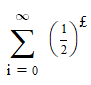
Close, but the £ symbol should be i.

Don’t know 1;
2 is the infinite sum sibeen posted,
3 is the html text for the number 3,
4 is the number that, multiplied by 2 (mod 7) gives 1,
5 is from the golden ratio: φ² = φ + 1,
6 is Γ(4),
7 used the fact that 0.999… = 1.0
8 is binary 1000,
9 is represented in base 4
10 is from probability: 5!/(3!*2!) (which can be written Γ(6)/(Γ(4)Γ(3))) = 120/12
11 is in hexadecimal, and
12 is one of the cube roots of 12³

btm said:

sibeen said:

2 looks like the equation

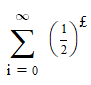
Close, but the £ symbol should be i.

Don’t know 1;
2 is the infinite sum sibeen posted,
3 is the html text for the number 3,
4 is the number that, multiplied by 2 (mod 7) gives 1,
5 is from the golden ratio: φ² = φ + 1,
6 is Γ(4),
7 used the fact that 0.999… = 1.0
8 is binary 1000,
9 is represented in base 4
10 is from probability: 5!/(3!*2!) (which can be written Γ(6)/(Γ(4)Γ(3))) = 120/12
11 is in hexadecimal, and
12 is one of the cube roots of 12³

Hmm, I tried ‘i’ but mathcad evaluated it as basically infinity.

btm said:

Don’t know 1;

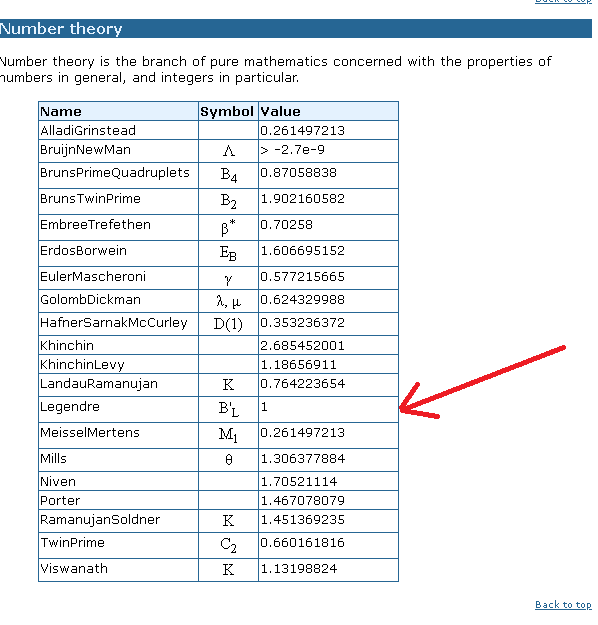
sibeen said:

btm said:

sibeen said:

2 looks like the equation

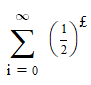
Close, but the £ symbol should be i.

Don’t know 1;
2 is the infinite sum sibeen posted,
3 is the html text for the number 3,
4 is the number that, multiplied by 2 (mod 7) gives 1,
5 is from the golden ratio: φ² = φ + 1,
6 is Γ(4),
7 used the fact that 0.999… = 1.0
8 is binary 1000,
9 is represented in base 4
10 is from probability: 5!/(3!*2!) (which can be written Γ(6)/(Γ(4)Γ(3))) = 120/12
11 is in hexadecimal, and
12 is one of the cube roots of 12³

Hmm, I tried ‘i’ but mathcad evaluated it as basically infinity.

It’s fairly easy to prove using the binomial theorem.
(1 – ½)^-1 = 1 + ½ + ½² + ½³ + ½⁴ + …
But (1 – ½)^-1 = ½^-1 = 2, so the infinite sum evaluates to 2.

Well picked up, esselte :)

btm said:

sibeen said:

btm said:

Close, but the £ symbol should be i.

Don’t know 1;
2 is the infinite sum sibeen posted,
3 is the html text for the number 3,
4 is the number that, multiplied by 2 (mod 7) gives 1,
5 is from the golden ratio: φ² = φ + 1,
6 is Γ(4),
7 used the fact that 0.999… = 1.0
8 is binary 1000,
9 is represented in base 4
10 is from probability: 5!/(3!*2!) (which can be written Γ(6)/(Γ(4)Γ(3))) = 120/12
11 is in hexadecimal, and
12 is one of the cube roots of 12³

Hmm, I tried ‘i’ but mathcad evaluated it as basically infinity.

It’s fairly easy to prove using the binomial theorem.
(1 – ½)^-1 = 1 + ½ + ½² + ½³ + ½⁴ + …
But (1 – ½)^-1 = ½^-1 = 2, so the infinite sum evaluates to 2.

Does a facepalm

I needed to solve symbolically – D’oh.

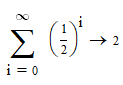
esselte said:

btm said:

Don’t know 1;

Thanks esselte.

btm said:

10 is from probability: 5!/(3!*2!) (which can be written Γ(6)/(Γ(4)Γ(3))) = 120/12

I’d never seen a combination expressed that way before. I probably have, but so long ago that I’ve forgotten :) I remember the form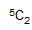

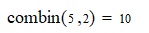
btm said:

esselte said:

btm said:

Don’t know 1;

Thanks esselte.

Even though I have a maths degree, I know significantly less maths than btm and esselte. We should have more maths on the forum.