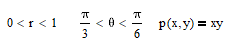Date: 21/01/2019 11:46:03
From: Spiny Norman
ID: 1333225
Subject: Integrals 2
I don’t really know where to start with this one – Though I can do the first squiggly line that has a zero at the bottom and one at the top, and the second squiggly line thing that has pi-on-three on the bottom and pi-on-six at the top.
The bit in between that and the answer is what I’m stuck on . Any suggestions please?
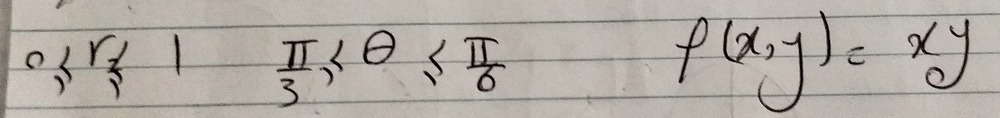
Date: 21/01/2019 11:57:00
From: sibeen
ID: 1333229
Subject: re: Integrals 2
Spiny Norman said:
Any suggestions please?
I’m just checking in and will be out the rest of the day – moving house – but maybe, just maybe, you could show the actual equations.
Date: 21/01/2019 11:57:23
From: Spiny Norman
ID: 1333230
Subject: re: Integrals 2
sibeen said:
Spiny Norman said:
Any suggestions please?
I’m just checking in and will be out the rest of the day – moving house – but maybe, just maybe, you could show the actual equations.
That’s all there is.
Date: 21/01/2019 12:01:19
From: The Rev Dodgson
ID: 1333233
Subject: re: Integrals 2
Spiny Norman said:
I don’t really know where to start with this one – Though I can do the first squiggly line that has a zero at the bottom and one at the top, and the second squiggly line thing that has pi-on-three on the bottom and pi-on-six at the top.
The bit in between that and the answer is what I’m stuck on . Any suggestions please?
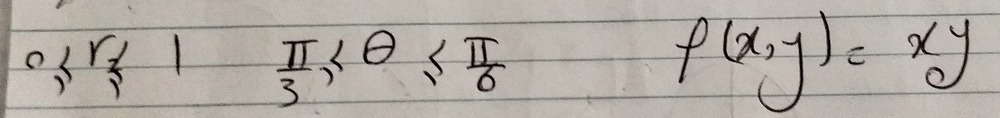
x = r.Cos(theta) and y =r.Sin(theta)
so xy = r^2.(Cos(theta).Sin(theta))
and integral dr from 0 to 1 = r^3/3.(Cos(theta).Sin(theta))
So you just need to integrate that with respect to theta.
Date: 21/01/2019 12:17:54
From: sibeen
ID: 1333241
Subject: re: Integrals 2
Spiny Norman said:
sibeen said:
Spiny Norman said:
Any suggestions please?
I’m just checking in and will be out the rest of the day – moving house – but maybe, just maybe, you could show the actual equations.
That’s all there is.
All I can see is:
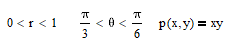
Date: 21/01/2019 12:18:27
From: Spiny Norman
ID: 1333242
Subject: re: Integrals 2
The Rev Dodgson said:
x = r.Cos(theta) and y =r.Sin(theta)
so xy = r^2.(Cos(theta).Sin(theta))
and integral dr from 0 to 1 = r^3/3.(Cos(theta).Sin(theta))
So you just need to integrate that with respect to theta.
So like this?
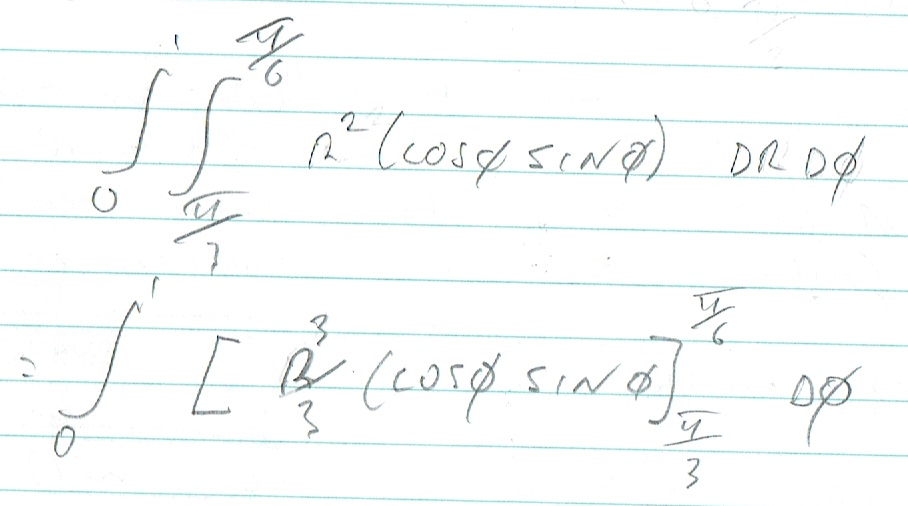
Date: 21/01/2019 12:19:01
From: Spiny Norman
ID: 1333243
Subject: re: Integrals 2
sibeen said:
Spiny Norman said:
sibeen said:
I’m just checking in and will be out the rest of the day – moving house – but maybe, just maybe, you could show the actual equations.
That’s all there is.
All I can see is:
Yep that’s right.xxxxxxxxxxxx
Date: 21/01/2019 12:19:59
From: Spiny Norman
ID: 1333245
Subject: re: Integrals 2
Dunno where all the x’s came from sorry.
Date: 21/01/2019 12:21:42
From: The Rev Dodgson
ID: 1333248
Subject: re: Integrals 2
Spiny Norman said:
The Rev Dodgson said:
x = r.Cos(theta) and y =r.Sin(theta)
so xy = r^2.(Cos(theta).Sin(theta))
and integral dr from 0 to 1 = r^3/3.(Cos(theta).Sin(theta))
So you just need to integrate that with respect to theta.
So like this?
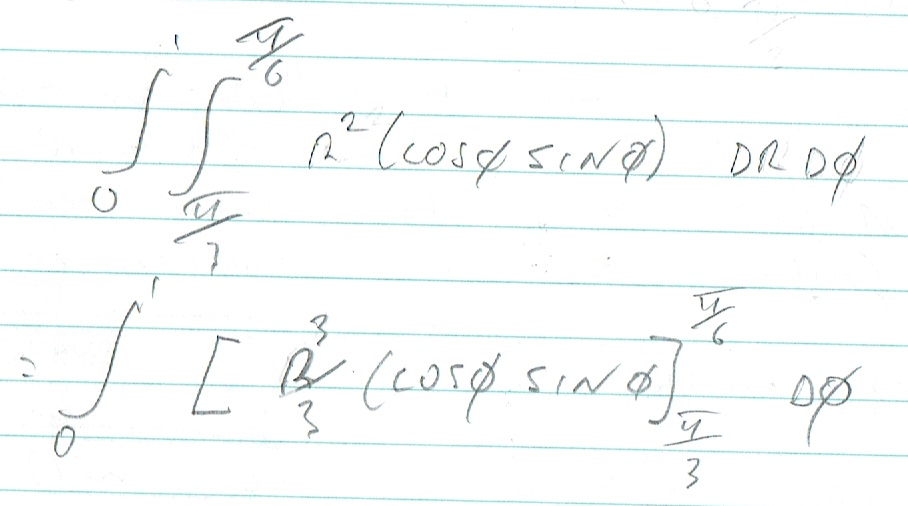
Looks good to me.
But check your result with a numerical integration :)
Date: 21/01/2019 12:28:41
From: The Rev Dodgson
ID: 1333253
Subject: re: Integrals 2
Spiny Norman said:
I don’t really know where to start with this one – Though I can do the first squiggly line that has a zero at the bottom and one at the top, and the second squiggly line thing that has pi-on-three on the bottom and pi-on-six at the top.
The bit in between that and the answer is what I’m stuck on . Any suggestions please?
Just noticed:
How can Theta be greater than Pi/3 but less than Pi/6?
Date: 21/01/2019 12:32:23
From: Spiny Norman
ID: 1333257
Subject: re: Integrals 2
The Rev Dodgson said:
Spiny Norman said:
I don’t really know where to start with this one – Though I can do the first squiggly line that has a zero at the bottom and one at the top, and the second squiggly line thing that has pi-on-three on the bottom and pi-on-six at the top.
The bit in between that and the answer is what I’m stuck on . Any suggestions please?
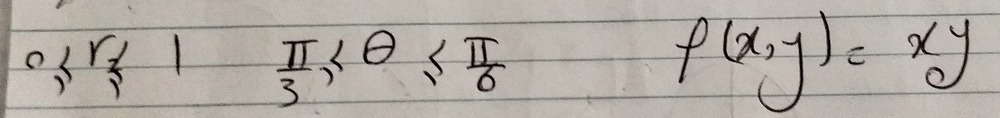
Just noticed:
How can Theta be greater than Pi/3 but less than Pi/6?
I didn’t write it, maybe the arc goes around the long way.
Date: 21/01/2019 12:48:42
From: The Rev Dodgson
ID: 1333276
Subject: re: Integrals 2
Spiny Norman said:
The Rev Dodgson said:
Spiny Norman said:
I don’t really know where to start with this one – Though I can do the first squiggly line that has a zero at the bottom and one at the top, and the second squiggly line thing that has pi-on-three on the bottom and pi-on-six at the top.
The bit in between that and the answer is what I’m stuck on . Any suggestions please?
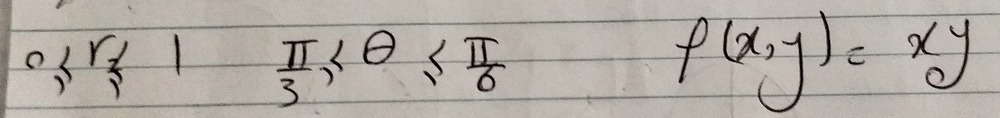
Just noticed:
How can Theta be greater than Pi/3 but less than Pi/6?
I didn’t write it, maybe the arc goes around the long way.
If it’s going round the long way wouldn’t it be pi/3 < Theta < (2pi + pi/6)?
Is there someone you can check with?
Date: 21/01/2019 13:57:15
From: mollwollfumble
ID: 1333306
Subject: re: Integrals 2
Has it been mentioned that dx * dy = r * dr * dθ ?
Don’t forget that extra factor of r.
ie.
∫ dy ∫ ρ dx = ∫ dx ∫ ρ dy = ∫ dθ ∫ ρ r dr = ∫ r dr ∫ ρ dθ
In this case you can integrate in either r first or θ first.
Date: 21/01/2019 14:43:54
From: sibeen
ID: 1333321
Subject: re: Integrals 2
Ahh, I see where I was going wrong here….I was being stupid :)
In my defence I am reasonably unintelligent and haven’t done double integrals in many a year.
Date: 21/01/2019 14:49:17
From: btm
ID: 1333324
Subject: re: Integrals 2
Spiny Norman said:
The Rev Dodgson said:
x = r.Cos(theta) and y =r.Sin(theta)
so xy = r^2.(Cos(theta).Sin(theta))
and integral dr from 0 to 1 = r^3/3.(Cos(theta).Sin(theta))
So you just need to integrate that with respect to theta.
So like this?
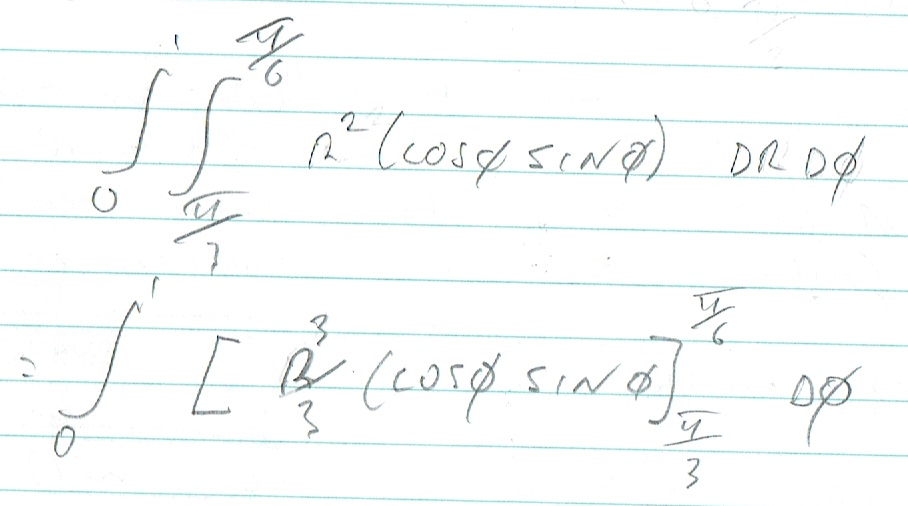
No, you’ve got the order of integration backwards (the order itself is not important (usually), but the application of limits is.) You’ve integrated over r, but applied the limits of dθ; the numbers on the RHS square brackets should be 0 (lower) and 1 (upper), and the π/3 and π/6 values should still be on the integral symbol.
Date: 21/01/2019 15:07:58
From: The Rev Dodgson
ID: 1333331
Subject: re: Integrals 2
btm said:
Spiny Norman said:
The Rev Dodgson said:
x = r.Cos(theta) and y =r.Sin(theta)
so xy = r^2.(Cos(theta).Sin(theta))
and integral dr from 0 to 1 = r^3/3.(Cos(theta).Sin(theta))
So you just need to integrate that with respect to theta.
So like this?
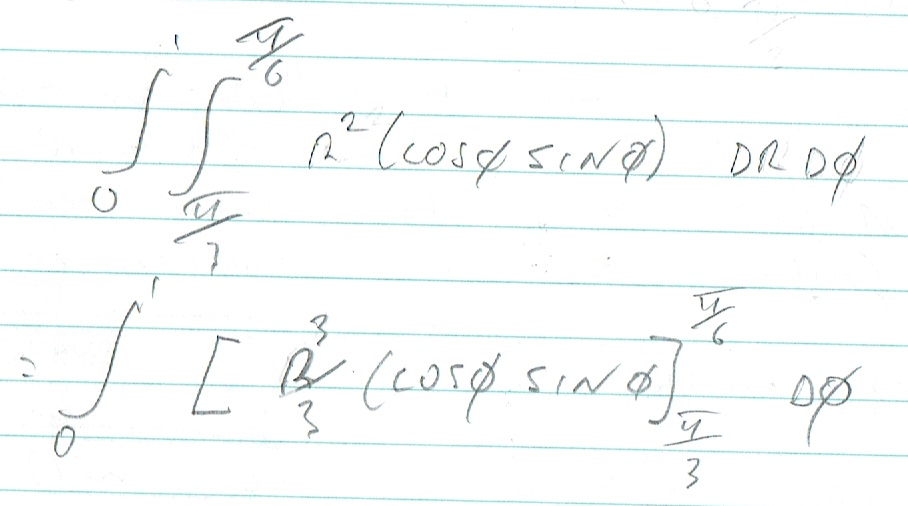
No, you’ve got the order of integration backwards (the order itself is not important (usually), but the application of limits is.) You’ve integrated over r, but applied the limits of dθ; the numbers on the RHS square brackets should be 0 (lower) and 1 (upper), and the π/3 and π/6 values should still be on the integral symbol.
oops.
Well spotted.
Date: 21/01/2019 17:14:13
From: mollwollfumble
ID: 1333362
Subject: re: Integrals 2
Order of integration doesn’t matter here.
What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.
Date: 21/01/2019 17:28:08
From: The Rev Dodgson
ID: 1333372
Subject: re: Integrals 2
All about integrating Cos(theta)Sin(theta):
https://mindyourdecisions.com/blog/2015/08/09/the-perplexing-integral-of-sin-xcos-x-sunday-puzzle/
(a bit long, but it does give three equivalent solutions).
Date: 21/01/2019 19:19:54
From: Spiny Norman
ID: 1333478
Subject: re: Integrals 2
Just got back.
Have read the thread.
Can someone please post how the working goes, then the answer?
Date: 21/01/2019 19:40:00
From: The Rev Dodgson
ID: 1333481
Subject: re: Integrals 2
Spiny Norman said:
Just got back.
Have read the thread.
Can someone please post how the working goes, then the answer?
Spiny Norman said:
Just got back.
Have read the thread.
Can someone please post how the working goes, then the answer?
The integral was as your last post, but with the limits swapped, as pointed out by btm.
The integral of sin(theta)cos(theta) is in the link I posted. Just use the first one they give if you don’t want to read the whole thing.
That should give you enough to get the answer.
Date: 21/01/2019 19:54:40
From: dv
ID: 1333486
Subject: re: Integrals 2
I haven’t read thread so sorry if already done.
BTW it is a bit weird that the end theta is lower than the start theta but whatevs. This means the answer will be negative.
0 <= r < = 1
pi/3 <= theta <= pi/6
f(x,y) = xy = r^2 cos(theta)*sin(theta)
so we want
int{theta = from pi/3 to pi/6, int{ r = from 0 to 1, r^2 cos(theta)*sin(theta)}}
if we integrate by r first:
int{theta = from pi/3 to pi/6 }
int{theta = from pi/3 to pi/6, (1/3 cos(theta)*sin(theta)} (by substituting and subtracting)
To integrate cos(theta)*sin(theta) you could use integration by parts or any number of other ways but anyway the integral of cos(theta)*sin(theta) is 1/2 (sin theta)^2
1/6 (0.25 – 0.75) (sub and sub)
= -1/12
I hope it’s right!
Date: 21/01/2019 19:56:17
From: Spiny Norman
ID: 1333487
Subject: re: Integrals 2
dv said:
I haven’t read thread so sorry if already done.
BTW it is a bit weird that the end theta is lower than the start theta but whatevs. This means the answer will be negative.
0 <= r < = 1
pi/3 <= theta <= pi/6
f(x,y) = xy = r^2 cos(theta)*sin(theta)
so we want
int{theta = from pi/3 to pi/6, int{ r = from 0 to 1, r^2 cos(theta)*sin(theta)}}
if we integrate by r first:
int{theta = from pi/3 to pi/6 }
int{theta = from pi/3 to pi/6, (1/3 cos(theta)*sin(theta)} (by substituting and subtracting)
To integrate cos(theta)*sin(theta) you could use integration by parts or any number of other ways but anyway the integral of cos(theta)*sin(theta) is 1/2 (sin theta)^2
1/6 (0.25 – 0.75) (sub and sub)
= -1/12
I hope it’s right!
I have no idea. :( Thanks anyway.
Date: 21/01/2019 19:57:38
From: Spiny Norman
ID: 1333488
Subject: re: Integrals 2
The Rev Dodgson said:
The integral was as your last post, but with the limits swapped, as pointed out by btm.
The integral of sin(theta)cos(theta) is in the link I posted. Just use the first one they give if you don’t want to read the whole thing.
That should give you enough to get the answer.
Okay I swapped them over and fed it into here
Still confusing as hell. Maybe I’ll try swapping over the integrals and d thingies and see how that goes.
Date: 21/01/2019 19:58:05
From: dv
ID: 1333489
Subject: re: Integrals 2
We can make it a bit simpler just by separating the two variables, which we can do because the limits don’t involve each other and the function is just a product of two variables.
Date: 21/01/2019 20:03:04
From: Spiny Norman
ID: 1333490
Subject: re: Integrals 2
dv said:
We can make it a bit simpler just by separating the two variables, which we can do because the limits don’t involve each other and the function is just a product of two variables.
I have come to a better solution – Just tell the tutor that I don’t know how to do it. I know you guys find this stuff fairly easy but I’m sorry I just don’t. It’s been about 35 years since I went to school and we never did any calculus then either, unlike the senior school kids these days.
Thanks for trying anyway.
Date: 21/01/2019 20:08:07
From: dv
ID: 1333494
Subject: re: Integrals 2

That’s what I get
Date: 21/01/2019 20:08:46
From: Spiny Norman
ID: 1333496
Subject: re: Integrals 2
dv said:

That’s what I get
Yeah the site I linked to gets the same answer, ta.
Date: 21/01/2019 20:13:36
From: The Rev Dodgson
ID: 1333499
Subject: re: Integrals 2
dv said:
I haven’t read thread so sorry if already done.
BTW it is a bit weird that the end theta is lower than the start theta but whatevs. This means the answer will be negative.
0 <= r < = 1
pi/3 <= theta <= pi/6
f(x,y) = xy = r^2 cos(theta)*sin(theta)
so we want
int{theta = from pi/3 to pi/6, int{ r = from 0 to 1, r^2 cos(theta)*sin(theta)}}
if we integrate by r first:
int{theta = from pi/3 to pi/6 }
int{theta = from pi/3 to pi/6, (1/3 cos(theta)*sin(theta)} (by substituting and subtracting)
To integrate cos(theta)*sin(theta) you could use integration by parts or any number of other ways but anyway the integral of cos(theta)*sin(theta) is 1/2 (sin theta)^2
1/6 (0.25 – 0.75) (sub and sub)
= -1/12
I hope it’s right!
That’s what I got.
Date: 21/01/2019 20:14:37
From: dv
ID: 1333500
Subject: re: Integrals 2
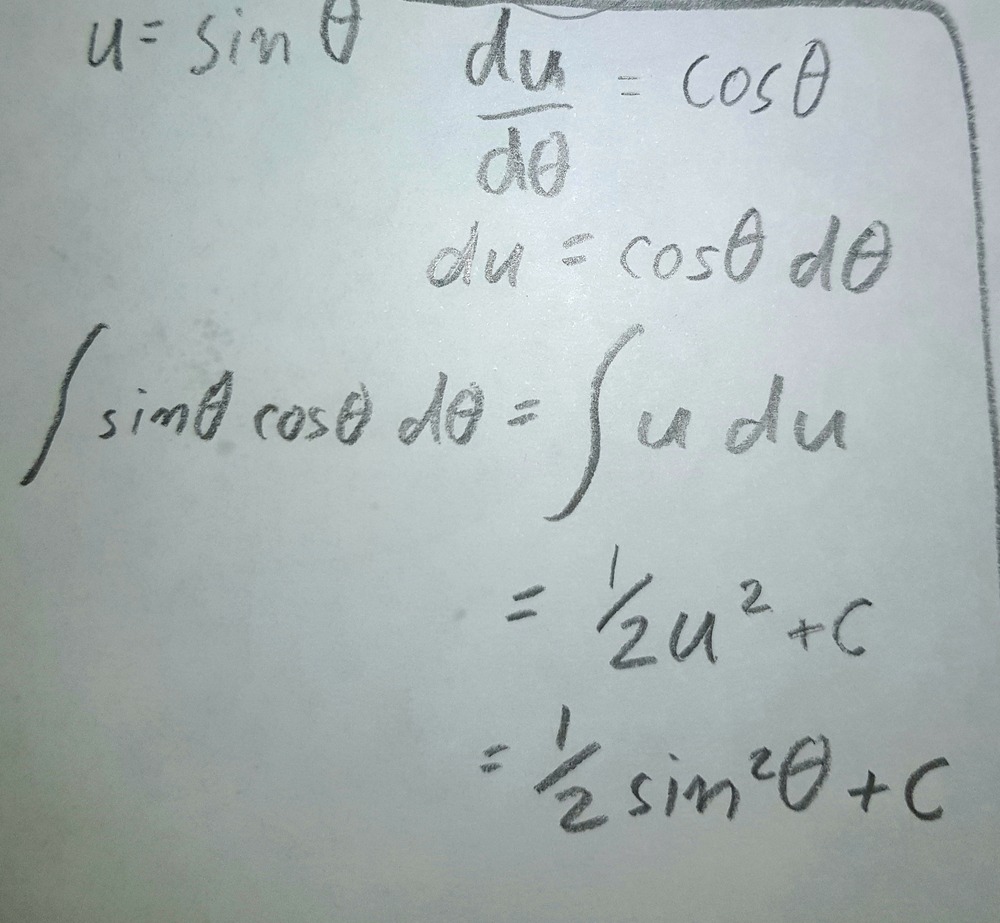
And here’s a little side bar on one way of working out the integral of sin theta cos theta.
The reason you might choose this method is that the integrand is a product of a function (sin theta) and its derivative (cos theta).
Date: 21/01/2019 20:17:43
From: dv
ID: 1333502
Subject: re: Integrals 2
Spiny Norman said:
dv said:
We can make it a bit simpler just by separating the two variables, which we can do because the limits don’t involve each other and the function is just a product of two variables.
I have come to a better solution – Just tell the tutor that I don’t know how to do it.
Well that’s always an option.
Date: 21/01/2019 20:17:50
From: The Rev Dodgson
ID: 1333503
Subject: re: Integrals 2
Spiny Norman said:
I know you guys find this stuff fairly easy
I wouldn’t say that.
I just happen to have been working on some spreadsheet functions to do multiple linear integration, so it fits in with that.
Date: 21/01/2019 20:19:07
From: sibeen
ID: 1333505
Subject: re: Integrals 2
The Rev Dodgson said:
Spiny Norman said:
I know you guys find this stuff fairly easy
I wouldn’t say that.
I just happen to have been working on some spreadsheet functions to do multiple linear integration, so it fits in with that.
I had to be given a major hint to have any idea as to what was being asked.
Date: 21/01/2019 20:20:11
From: Spiny Norman
ID: 1333507
Subject: re: Integrals 2
The Rev Dodgson said:
Spiny Norman said:
I know you guys find this stuff fairly easy
I wouldn’t say that.
I just happen to have been working on some spreadsheet functions to do multiple linear integration, so it fits in with that.
What I’ll probably end up doing is just not worry about this circular stuff and spend more time on the things that I can do.
Date: 21/01/2019 20:25:14
From: Peak Warming Man
ID: 1333509
Subject: re: Integrals 2
Spiny Norman said:
The Rev Dodgson said:
Spiny Norman said:
I know you guys find this stuff fairly easy
I wouldn’t say that.
I just happen to have been working on some spreadsheet functions to do multiple linear integration, so it fits in with that.
What I’ll probably end up doing is just not worry about this circular stuff and spend more time on the things that I can do.
Do what you can in the Maths exam and hand it in with a folded Mawson inside.
Date: 21/01/2019 21:07:33
From: The Rev Dodgson
ID: 1333547
Subject: re: Integrals 2
Mollwoll said something and we missed it:
“What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.”
I think the result should be -1/16, not -1/12.
Date: 21/01/2019 21:18:51
From: sibeen
ID: 1333552
Subject: re: Integrals 2
The Rev Dodgson said:
Mollwoll said something and we missed it:
“What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.”
I think the result should be -1/16, not -1/12.
I’m obviously missing something, why r3
Date: 21/01/2019 21:36:09
From: dv
ID: 1333553
Subject: re: Integrals 2
sibeen said:
The Rev Dodgson said:
Mollwoll said something and we missed it:
“What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.”
I think the result should be -1/16, not -1/12.
I’m obviously missing something, why r3
It would be good to see the full question as asked, rather than just the bounding params.
Date: 21/01/2019 21:43:55
From: dv
ID: 1333558
Subject: re: Integrals 2
dv said:
sibeen said:
The Rev Dodgson said:
Mollwoll said something and we missed it:
“What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.”
I think the result should be -1/16, not -1/12.
I’m obviously missing something, why r3
It would be good to see the full question as asked, rather than just the bounding params.
Specifically:
are we being asked to integrate this function with respect to theta and r between the specified limits
or
are we being asked to integrate this function over the area _indicated?
Date: 21/01/2019 21:49:06
From: The Rev Dodgson
ID: 1333564
Subject: re: Integrals 2
dv said:
dv said:
sibeen said:
I’m obviously missing something, why r3
It would be good to see the full question as asked, rather than just the bounding params.
Specifically:
are we being asked to integrate this function with respect to theta and r between the specified limits
or
are we being asked to integrate this function over the area _indicated?
Fair question.
SN doesn’t have any more info, but my interpretation would now be that we should be integrating xy over the area of the circular segment defined by pi/6, pi/3 and r= 1.
Date: 21/01/2019 21:49:39
From: dv
ID: 1333565
Subject: re: Integrals 2
The Rev Dodgson said:
dv said:
dv said:
It would be good to see the full question as asked, rather than just the bounding params.
Specifically:
are we being asked to integrate this function with respect to theta and r between the specified limits
or
are we being asked to integrate this function over the area _indicated?
Fair question.
SN doesn’t have any more info, but my interpretation would now be that we should be integrating xy over the area of the circular segment defined by pi/6, pi/3 and r= 1.
I suppose that is most likely.
Date: 21/01/2019 21:51:39
From: sibeen
ID: 1333568
Subject: re: Integrals 2
dv said:
The Rev Dodgson said:
dv said:
Specifically:
are we being asked to integrate this function with respect to theta and r between the specified limits
or
are we being asked to integrate this function over the area _indicated?
Fair question.
SN doesn’t have any more info, but my interpretation would now be that we should be integrating xy over the area of the circular segment defined by pi/6, pi/3 and r= 1.
I suppose that is most likely.
So why then the pi/3 to pi/6 kerfuffle?
Date: 21/01/2019 21:53:00
From: The Rev Dodgson
ID: 1333569
Subject: re: Integrals 2
sibeen said:
The Rev Dodgson said:
Mollwoll said something and we missed it:
“What matters is that you’re integrating r * rho in polar coordinates.
So that’s an integral of r^3 cos sin not r^2 cos sin.”
I think the result should be -1/16, not -1/12.
I’m obviously missing something, why r3
We are integrating a value with dimensions L^2 over an area, so the result must have dimensions of L^4.
Date: 21/01/2019 21:54:07
From: The Rev Dodgson
ID: 1333570
Subject: re: Integrals 2
sibeen said:
dv said:
The Rev Dodgson said:
Fair question.
SN doesn’t have any more info, but my interpretation would now be that we should be integrating xy over the area of the circular segment defined by pi/6, pi/3 and r= 1.
I suppose that is most likely.
So why then the pi/3 to pi/6 kerfuffle?
I think that’s either a mistake or a clever ploy to confuse the unwary.
Date: 21/01/2019 21:55:14
From: dv
ID: 1333571
Subject: re: Integrals 2
sibeen said:
dv said:
The Rev Dodgson said:
Fair question.
SN doesn’t have any more info, but my interpretation would now be that we should be integrating xy over the area of the circular segment defined by pi/6, pi/3 and r= 1.
I suppose that is most likely.
So why then the pi/3 to pi/6 kerfuffle?
Well perhaps someone simply made a mistake.
Date: 21/01/2019 21:56:31
From: dv
ID: 1333572
Subject: re: Integrals 2
But anyway, I concur with moll and Rev. IF indeed they are asking to integrate the function over the area, then it is 1/16. It they are asking to integrate the function, with respect to the stated variables, between the stated limits, then the answers is -1/12.
Date: 21/01/2019 22:00:09
From: Spiny Norman
ID: 1333573
Subject: re: Integrals 2
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
Date: 21/01/2019 22:01:08
From: sibeen
ID: 1333574
Subject: re: Integrals 2
Spiny Norman said:
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
Ta.
Date: 21/01/2019 22:08:30
From: The Rev Dodgson
ID: 1333577
Subject: re: Integrals 2
Spiny Norman said:
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
Well I hope he gets it right :)
Date: 21/01/2019 22:31:52
From: The Rev Dodgson
ID: 1333578
Subject: re: Integrals 2
I have now done a numerical double integration of xy over the limits:
x: 0 to 0.866025404
y: tan(pi/6)*x to tan(pi/3)*x if x < 0.5 else (1-x^2)^0.5
That defines a circular segment of radius 1 with centre at the origin and sides at pi/6 (30 degrees) and pi/3 (60 degrees).
and the result is
drumroll …….
0.0625 = 1/16
I have also learned how to write an if then else statement on a single line in Python, so it was all worthwhile.
Date: 21/01/2019 22:52:11
From: dv
ID: 1333581
Subject: re: Integrals 2
SN, do you happen to remember the question being asked?
Date: 22/01/2019 06:29:18
From: Spiny Norman
ID: 1333592
Subject: re: Integrals 2
dv said:
SN, do you happen to remember the question being asked?
It’s in the first photo I posted, that’s all there is.
Date: 22/01/2019 18:34:55
From: sibeen
ID: 1333976
Subject: re: Integrals 2
Spiny Norman said:
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
drums fingers
Date: 22/01/2019 22:13:18
From: The Rev Dodgson
ID: 1334063
Subject: re: Integrals 2
sibeen said:
Spiny Norman said:
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
drums fingers
How are your fingers now?
Date: 22/01/2019 22:19:15
From: sibeen
ID: 1334066
Subject: re: Integrals 2
The Rev Dodgson said:
sibeen said:
Spiny Norman said:
Got another session with the tutor tomorrow at 4pm. The question will be reviewed and I’ll let you all know some time after that.
drums fingers
How are your fingers now?
Nubs.
Date: 23/01/2019 08:19:18
From: sibeen
ID: 1334154
Subject: re: Integrals 2
sibeen said:
The Rev Dodgson said:
sibeen said:
drums fingers
How are your fingers now?
Nubs.
This is tiring.
Date: 23/01/2019 08:21:40
From: roughbarked
ID: 1334156
Subject: re: Integrals 2
sibeen said:
sibeen said:
The Rev Dodgson said:
How are your fingers now?
Nubs.
This is tiring.
Should use drumsticks.
Date: 23/01/2019 08:23:01
From: Spiny Norman
ID: 1334157
Subject: re: Integrals 2
Sorry I forgot to post that yesterday’s tutorial was cancelled, it’s now on at 4 pm today.
Date: 23/01/2019 08:25:07
From: sibeen
ID: 1334159
Subject: re: Integrals 2
Date: 23/01/2019 20:15:08
From: Spiny Norman
ID: 1334518
Subject: re: Integrals 2
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
Date: 23/01/2019 20:17:07
From: The Rev Dodgson
ID: 1334521
Subject: re: Integrals 2
Spiny Norman said:
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
OK, but what’s the answer?
Date: 23/01/2019 20:18:23
From: roughbarked
ID: 1334525
Subject: re: Integrals 2
The Rev Dodgson said:
Spiny Norman said:
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
OK, but what’s the answer?
Try turning the paper around?
Date: 23/01/2019 20:23:11
From: sibeen
ID: 1334531
Subject: re: Integrals 2
The Rev Dodgson said:
Spiny Norman said:
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
OK, but what’s the answer?
Bill, there was an issue as to whether the answer was 1/12 or 1/16, and it depended upon actual question.
Date: 23/01/2019 20:27:21
From: dv
ID: 1334540
Subject: re: Integrals 2
sibeen said:
The Rev Dodgson said:
Spiny Norman said:
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
OK, but what’s the answer?
Bill, there was an issue as to whether the answer was 1/12 or 1/16, and it depended upon actual question.
To wit:
If he was asking you to integrate the function “over the area”, the answer is 1/16. If he was asking you to integrate the function with respect to the given variables, within the given bounds, then the answer is 1/12. Or rather -1/12, if we include the typo.
Date: 23/01/2019 20:34:10
From: Spiny Norman
ID: 1334550
Subject: re: Integrals 2
Don’t know for sure sorry, we didn’t work on it after that. I’m guessing it was area that he was after as the other questions were along those lines.
Date: 23/01/2019 20:37:15
From: roughbarked
ID: 1334552
Subject: re: Integrals 2
Anyway, I now know more about assigning numbers to functions than I ever did. Thanks.
Date: 24/01/2019 21:19:46
From: mollwollfumble
ID: 1335200
Subject: re: Integrals 2
Spiny Norman said:
The mystery is solved – When I pointed it out, he said, “oh yeah I got those back to front”.
So there ya go.
That makes more sense.