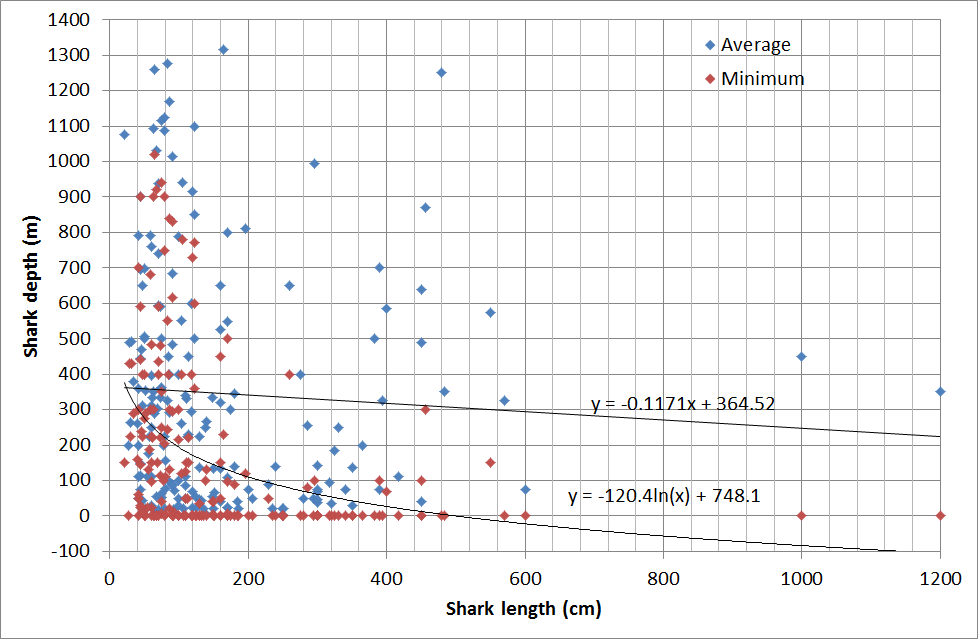
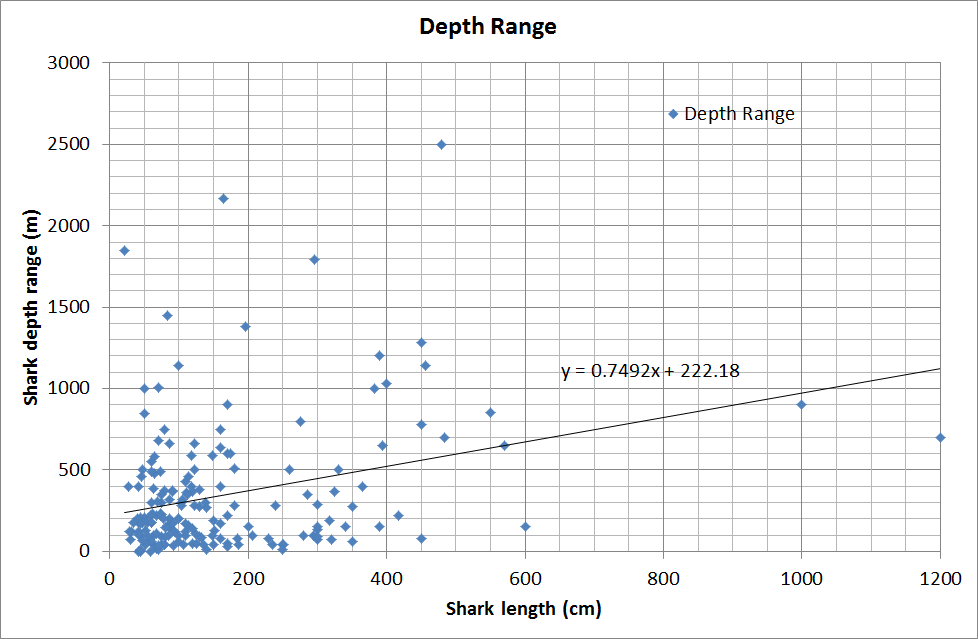
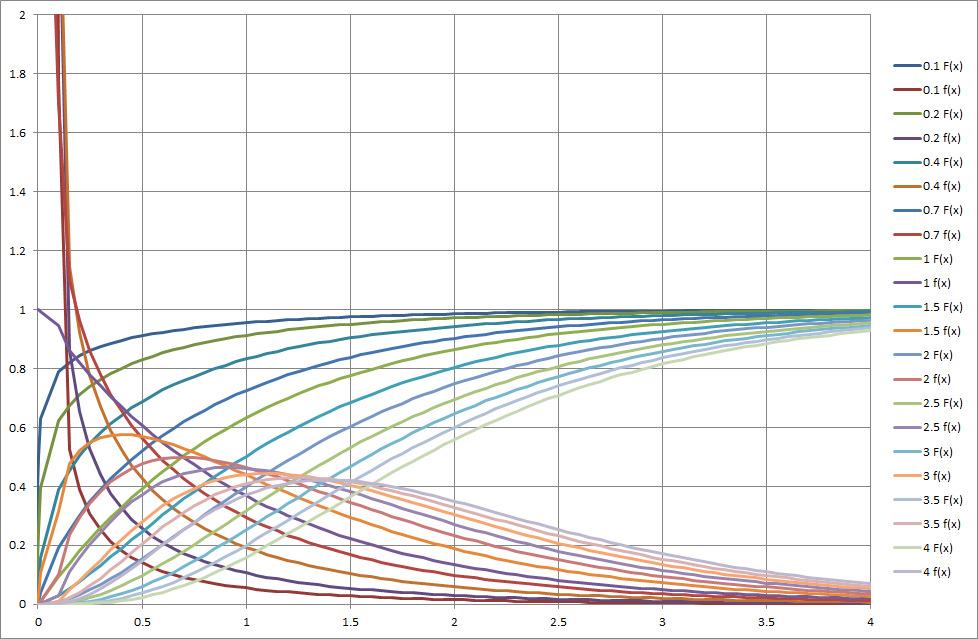
Reading “Sharks and Rays of Australia” book again, Last time, I was extremely impressed by how many new shark species have been found. This time, I thought I’d check out shark lengths and the depth that they live. Results from Excel spreadsheet.

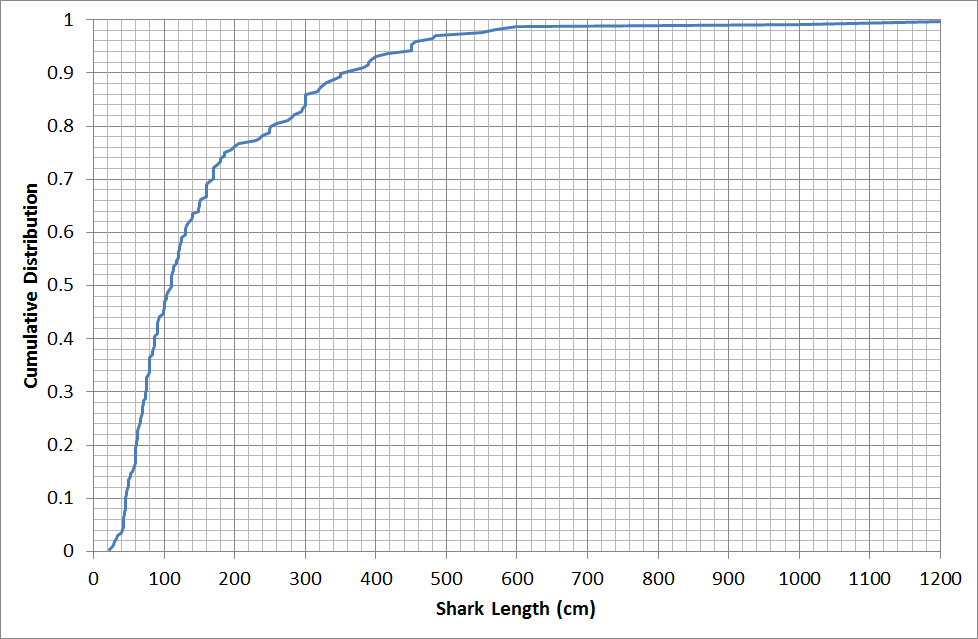
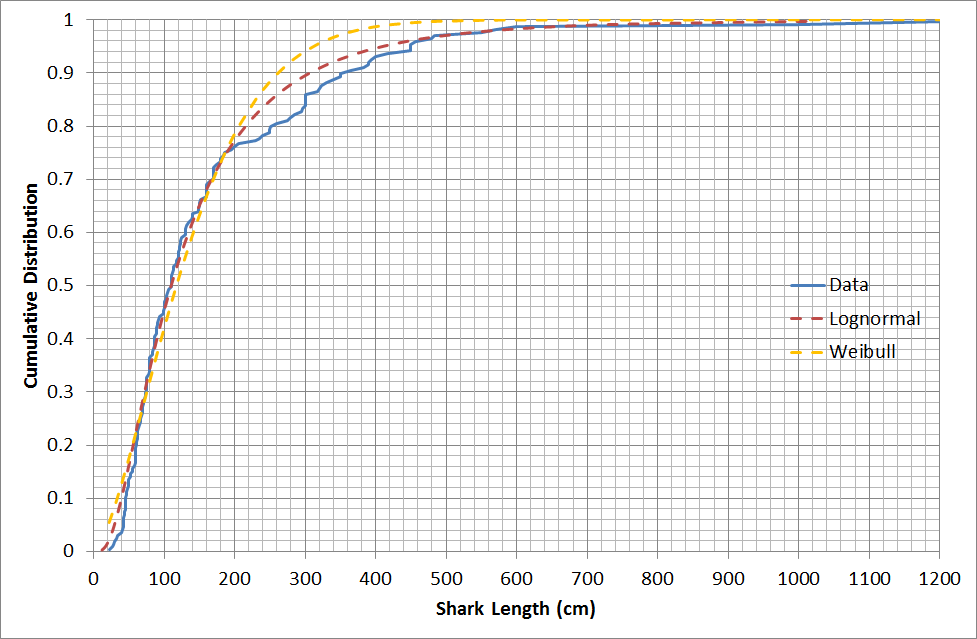
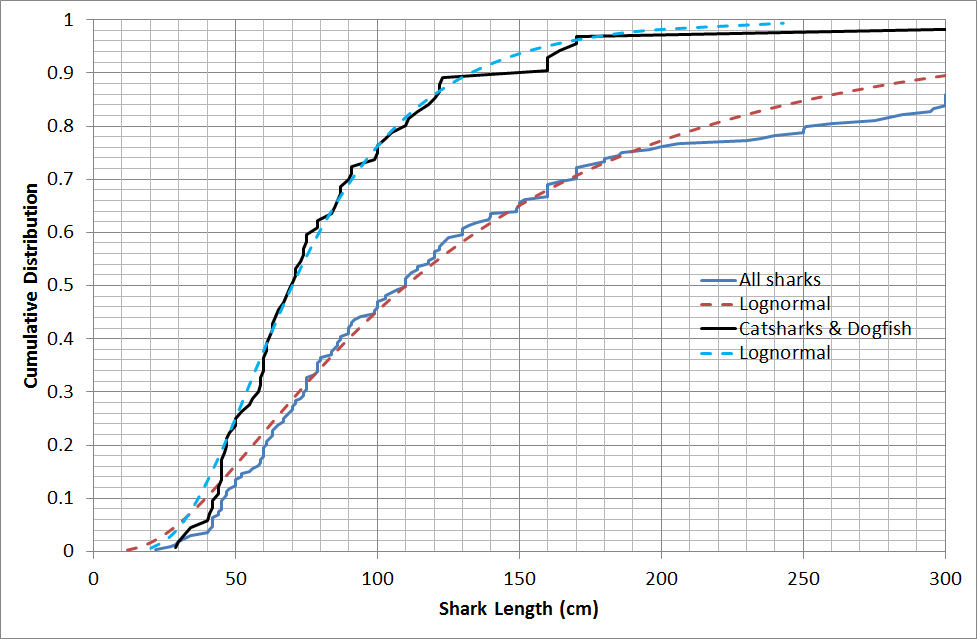
The median upper length for shark species (excluding rays and chimeras) is only 1.1 metres, largely because of the large numbers of small dogfish and catshark species.

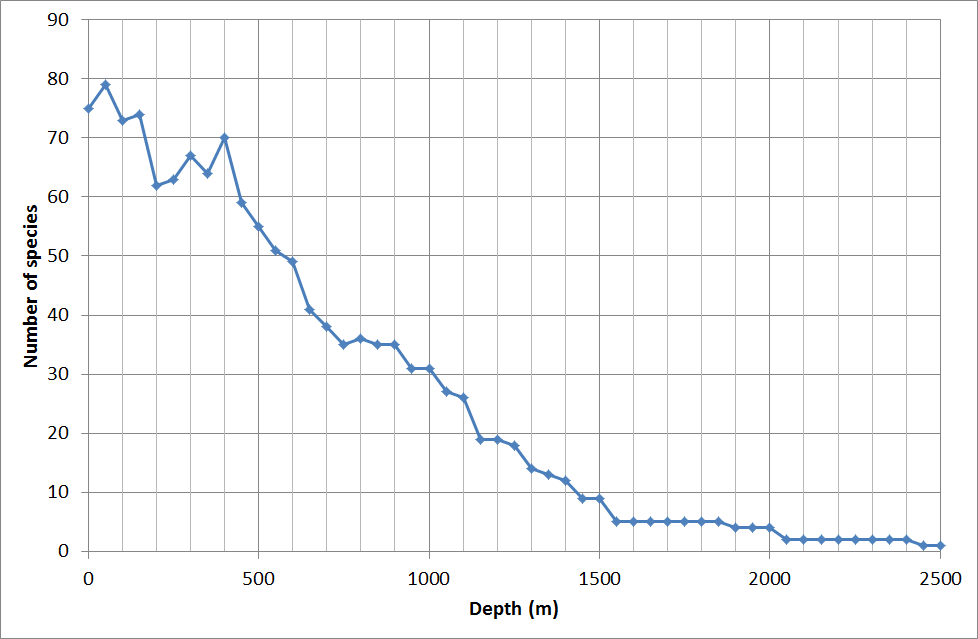
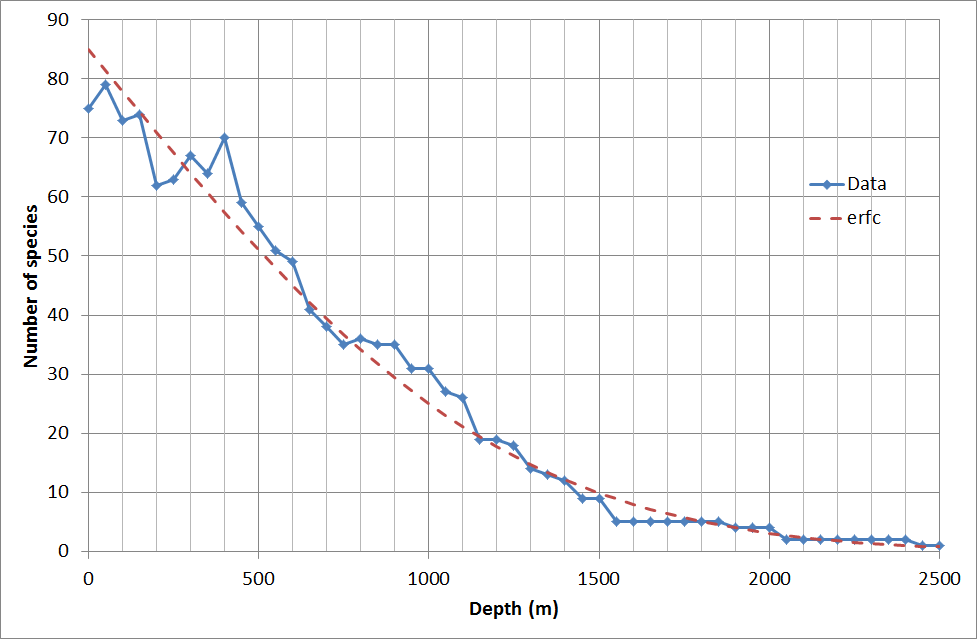
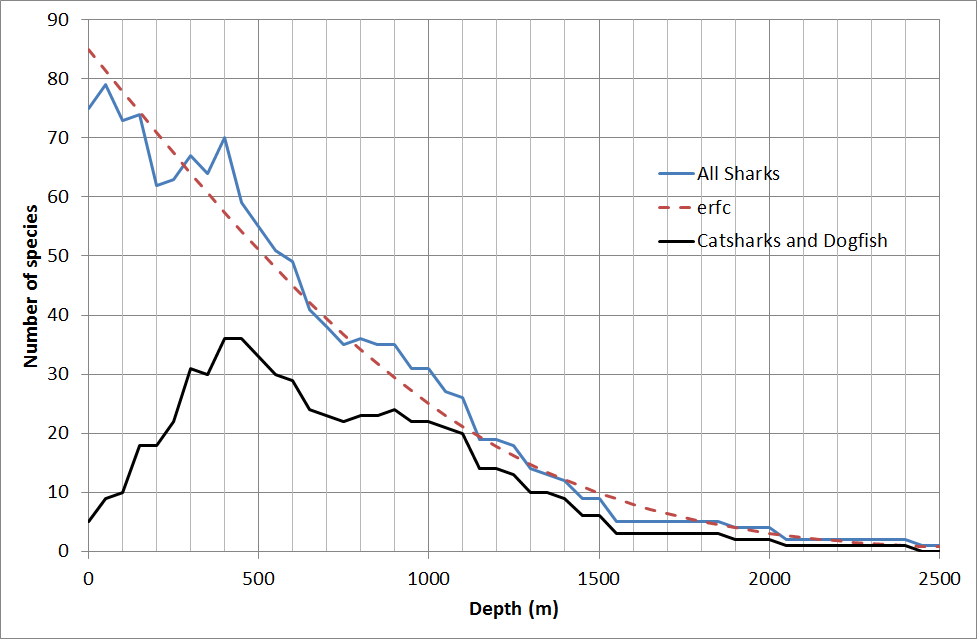
The number of shark species found at a depth of 700 m, which is really deep, is still 50% of the number of shark species found in surface waters.

The lognormal distribution is a better fit to the shark length data than the Weibull distribution.

The number of shark species vs depth is well fitted by the complementary error function

Catsharks, dogfish and similar account for about 43% of all sharks.

They are small, the median upper limit on length is 0.7 metres.

And they live at depth, mostly 400 to 500 metres deep, with a substantial number of species still at 1100 metres deep.

The size distribution is still lognormal, but the depth distribution is nothing like erfc.

mollwollfumble said:

Catsharks, dogfish and similar account for about 43% of all sharks.

They are small, the median upper limit on length is 0.7 metres.

And they live at depth, mostly 400 to 500 metres deep, with a substantial number of species still at 1100 metres deep.

The size distribution is still lognormal, but the depth distribution is nothing like erfc.

Could the shark distribution with depth be Gumbel, I wonder.

Hold on, that graph isn’t right. The line for n=1 looks like e ^-x not like 1 – e ^-x
Unless that’s the formula for the cumulative distribution.
If F(x) = 1 – e ^-x
then f(x) = dF(x)/dx = e ^-x
That must be what they mean.

Nice but can you plot depth v length?

dv said:

Nice but can you plot depth v length?

Will do. Here ‘tis. First thing I noticed was that average depth is practically independent of length, which came as a complete surprise because smaller sharks are seldom found on the surface. So I checked, and minimum depth decreases with length. The range of depths at which the shark lives increases as the shark size increases.

Gumbel distribution won’t do for depth, because f(x) has a nonzero finite value at the surface only for n=1.

Gumbel distribution.