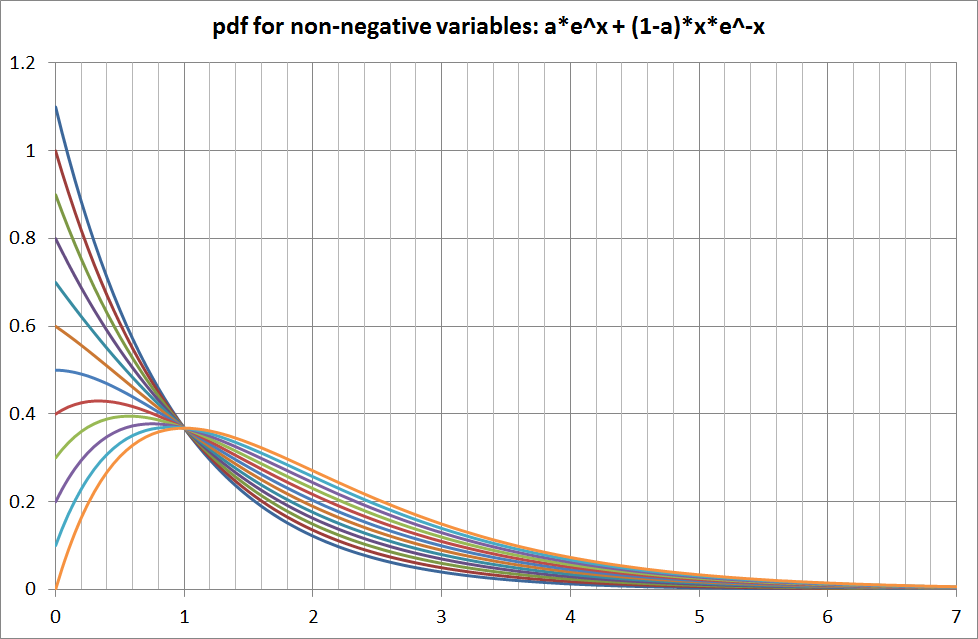
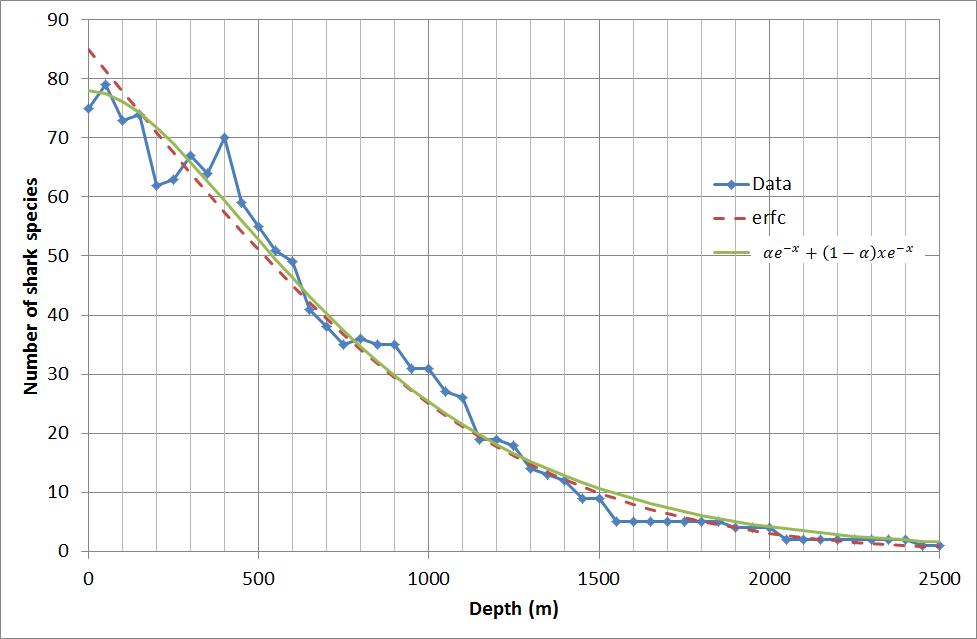
Does this probability distribution function pdf have a name? It looks like it could be quite useful. I was looking for a pdf to describe the variation of numbers of shark species (of different types) with depth, and neither truncated normal, gumbel, or weibull was a fit. A similar pdf could be used to describe perhaps wind speed for example.
a e -x +(1-a) x e -x
where 0 ≤ a ≤ 1.