This morning I was wondering how it was possible to measure the distance from a point on the surface of the Earth to the centre, and I realised that I have no idea how this was done before the days of satellites.

Can anyone enlighten me?

Measure the circumference and work back from there.

strolls off

sibeen said:

Measure the circumference and work back from there.

strolls off

you are an ideas man. not saying they are good ideas, just ideas.

Sibeen is correct. Here’s how it was first done.

https://en.wikipedia.org/wiki/Eratosthenes#Measurement_of_the_Earth’s_circumference

sibeen said:

Measure the circumference and work back from there.

strolls off

With what shall I measure it?

(Apart from which, I want the radius at a point, not averaged along a line.)

Michael V said:

Sibeen is correct. Here’s how it was first done.

https://en.wikipedia.org/wiki/Eratosthenes#Measurement_of_the_Earth’s_circumference

OK, I knew about Eratosthenes, but if (for instance) you wanted to measure the difference in radius between the Equator and the Poles, how would you do that?

Doesn’t answer my question, but interesting nonetheless:

Measuring the earth’s radius 1000 years ago

The Rev Dodgson said:

This morning I was wondering how it was possible to measure the distance from a point on the surface of the Earth to the centre, and I realised that I have no idea how this was done before the days of satellites.

Can anyone enlighten me?

Yes. Let’s move forward from the days of Eratosthenes to the controversy over whether the Earth was oblate or prolate. The method is the same, but more accurate.

Newton was claiming from his law of gravity that the Earth was oblate. In Paris, however, they thought that the Earth was prolate.

Enter an astronomer in South Africa. “Abbé Nicolas-Louis de Lacaille, formerly sometimes spelled de la Caille, was a French astronomer who named 15 out of the 88 constellations. From 1750-1754 he studied the sky at the Cape of Good Hope in present day South Africa. Lacaille observed over 10,000 stars using just a half-inch refractor.” He had accurately measured the distance from the vertical of stars in Paris and was doing the same down south.

Here is a picture of his telescope. He’s illustrated sighting through the roof at a star. He very accurately measured the angle off vertical of the same stars from South Africa, and so determine the latitude there. With the distance between the two he got the most accurate number for thevradius of the Earth to that date.

mollwollfumble said:

The Rev Dodgson said:

This morning I was wondering how it was possible to measure the distance from a point on the surface of the Earth to the centre, and I realised that I have no idea how this was done before the days of satellites.

Can anyone enlighten me?

Yes. Let’s move forward from the days of Eratosthenes to the controversy over whether the Earth was oblate or prolate. The method is the same, but more accurate.

Newton was claiming from his law of gravity that the Earth was oblate. In Paris, however, they thought that the Earth was prolate.

Enter an astronomer in South Africa. “Abbé Nicolas-Louis de Lacaille, formerly sometimes spelled de la Caille, was a French astronomer who named 15 out of the 88 constellations. From 1750-1754 he studied the sky at the Cape of Good Hope in present day South Africa. Lacaille observed over 10,000 stars using just a half-inch refractor.” He had accurately measured the distance from the vertical of stars in Paris and was doing the same down south.

Here is a picture of his telescope. He’s illustrated sighting through the roof at a star. He very accurately measured the angle off vertical of the same stars from South Africa, and so determine the latitude there. With the distance between the two he got the most accurate number for thevradius of the Earth to that date.

Thanks, my Bingeing didn’t find that.

But it’s still measuring the average radius over a long distance. How can we accurately measure the radius at a point (or a comparatively short distance)?

Also, any idea why the French thought the Earth would be prolate?

Slightly off topic, but this is interesting:

Hooke’s Memorandum on the development of orbital dynamics

vague memories – I thought when the Greeks first did it was something to do with measuring the angle of the sun (using a well) at two places at the same time, a known distance apart, and then working out from there.

The Rev Dodgson said:

Also, any idea why the French thought the Earth would be prolate?

Thanks, my Bingeing didn’t find that.

But it’s still measuring the average radius over a long distance. How can we accurately measure the radius at a point (or a comparatively short distance)?

> why the French thought the Earth would be prolate?

Found it. In a word, Cassini.

“Giovanni Domenico Cassini rejected Newton’s theory of gravity, after measurements (in about 1675) he conducted which wrongly suggested that the Earth was elongated at its poles. More than forty years of controversy about the subject were closed in favour of Newton’s theory after the measurements of the French Geodesic Mission (1736 to 1744) and the Lapponian expedition in 1737 led by Pierre Louis Moreau de Maupertuis”. Cassini probably had access to an astronomer called Jean Richer in French Guiana for information on which to base his calculations.

> How can we accurately measure the radius at a point (or a comparatively short distance)?

Alfred Russel Wallace did that.

In 1870, a Flat-Earth proponent named John Hampden offered a £500 wager in a magazine advertisement to anyone who could demonstrate a convex curvature in a body of water such as a river, canal, or lake. Wallace, intrigued by the challenge and short of money at the time, designed an experiment in which he set up two objects along a six-mile (10 km) stretch of canal. Both objects were at the same height above the water, and he mounted a telescope on a bridge at the same height above the water as well. When seen through the telescope, one object appeared higher than the other, showing the curvature of the earth.

> my Bingeing didn’t find that

I’m going from memory, so may have an anachronism in there. I have a book called “Parallax” about how astronomers failed to, and later succeeded in finding the distances to the nearest stars. I probably remembered it from that.

I’m trying to figure out when Ptolemy’s wrong radius was corrected.

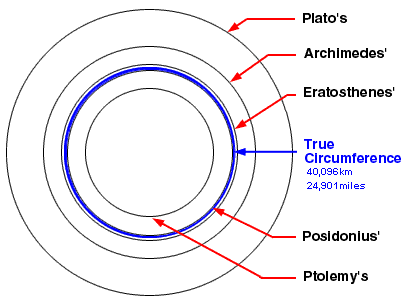
Eratosthenes got it right C100 BC
Others at about the same time got it wrong.
Ptolemy used the wrong radius in his Geography in 150 AD
Columbus was still using the wrong Ptolemy radius in 1502

Tycho by 1588 was collaborating with astronomers in different parts of Europe, but did he have the correct radius of the Earth? Tycho knew the distance to Saturn by 1602 (though not necessarily accurately).

Ah, here we go, https://en.wikipedia.org/wiki/History_of_geodesy

“Around AD 830 Caliph al-Ma’mun commissioned a group of astronomers led by Al-Khwarizmi to measure the distance from Tadmur (Palmyra) to Raqqa” They got the correct radius of the Earth.

“In 1505 the cosmographer and explorer Duarte Pacheco Pereira calculated the value of the degree of the meridian arc with a margin of error of only 4%, when the current error at the time varied between 7 and 15%.”

More on prolate in Paris here, too.

“Jean Picard performed the first modern meridian arc measurement in 1669–1670. He measured a baseline using wooden rods, a telescope … Jacques Cassini later continued Picard’s arc (Paris meridian arc) northward to Dunkirk and southward to the Spanish border. Cassini divided the measured arc into two parts, one northward from Paris, another southward. When he computed the length of a degree from both chains, he found that the length of one degree of latitude in the northern part of the chain was shorter than that in the southern part. This result, if correct, meant that the earth was not a sphere, but a prolate spheroid (taller than wide). However, this contradicted computations by Isaac Newton and Christiaan Huygens.”

The Rev Dodgson said:

sibeen said:

Measure the circumference and work back from there.

strolls off

With what shall I measure it?

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

dv said:

The Rev Dodgson said:

sibeen said:

Measure the circumference and work back from there.

strolls off

With what shall I measure it?

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

A watch or clock, could also be of assitance?

roughbarked said:

dv said:

The Rev Dodgson said:

With what shall I measure it?

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

dv said:

roughbarked said:

dv said:

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

https://en.wikipedia.org/wiki/Antikythera_mechanism

dv said:

roughbarked said:

dv said:

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

Didn’t they have clepsydras?

dv said:

roughbarked said:

dv said:

Well you could find a nice straight stretch of road and use the odometer of your car. Or you could use your basic surveying techniques using a series of line of sight measurements and some trigonometry. Or of near enough was good enough you could measure your pace and then pace it out (using astronomical navigation to keep a common direction) though again a nice flat path would aid this.

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

The Rev Dodgson said:

dv said:

roughbarked said:

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

there’s the nub.

The Rev Dodgson said:

With what shall I measure it?

with a ruler dear reverend, dear reverend, dear reverend. With a ruler dear reverend, measure it.

roughbarked said:

The Rev Dodgson said:

dv said:

Well the ancient Greeks did it without any timing devices other than the sun.

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

there’s the nub.

More specifically, I’m interested in how it was done in the 19th or first half 20th Centuries, or whenever the first reasonably accurate measurements were made.

ChrispenEvan said:

The Rev Dodgson said:

With what shall I measure it?

with a ruler dear reverend, dear reverend, dear reverend. With a ruler dear reverend, measure it.

Yes Harry B.

Tamb said:

ChrispenEvan said:

The Rev Dodgson said:

With what shall I measure it?

with a ruler dear reverend, dear reverend, dear reverend. With a ruler dear reverend, measure it.

Yes Harry B.

It is I suppose at least a reasonably relevant reference for a question about the measurement of a circle.

The Rev Dodgson said:

Tamb said:

ChrispenEvan said:

with a ruler dear reverend, dear reverend, dear reverend. With a ruler dear reverend, measure it.

Yes Harry B.

It is I suppose at least a reasonably relevant reference for a question about the measurement of a circle.

It would fit. er; within the circle that is.

The Rev Dodgson said:

dv said:

roughbarked said:

A watch or clock, could also be of assitance?

Well the ancient Greeks did it without any timing devices other than the sun.

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

Obviously the actual distance of a particular point on the Earth’s surface will depend on local topography. If you work out the “height” of mean sea level at your latitude, then again using surveying and trigonometry you can work out your actual distance from the earth’s centre. The shape of the earth, as defined by mean sea level, is an oblate spheroid, so in effect the way you would do it is to determine the statistics of that spheroid, work out your latitude, and work out the distance from centre to sea level at that latitude.

So in essence, given that you seem to accept in principle that you can measure the average radius over a path using primitive methods, the question you are asking is “how can I determine the statistics of the ellipticity of the earth without satellites”.

But the answer is basically the same. By measuring the change in angle with change in distance at various latitudes, you can calculate the shape of this spheroid. Newton discussed this phenomenon in Principia and it also gained some theoretical coverage by Arab authors during the Golden Age (though without any actual estimates, just the theory). Pretty good estimates of the shape of the spheroid had been made using astronomical measurements by the 1700s.

dv said:

The Rev Dodgson said:

dv said:

Well the ancient Greeks did it without any timing devices other than the sun.

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

Obviously the actual distance of a particular point on the Earth’s surface will depend on local topography. If you work out the “height” of mean sea level at your latitude, then again using surveying and trigonometry you can work out your actual distance from the earth’s centre. The shape of the earth, as defined by mean sea level, is an oblate spheroid, so in effect the way you would do it is to determine the statistics of that spheroid, work out your latitude, and work out the distance from centre to sea level at that latitude.

So in essence, given that you seem to accept in principle that you can measure the average radius over a path using primitive methods, the question you are asking is “how can I determine the statistics of the ellipticity of the earth without satellites”.

But the answer is basically the same. By measuring the change in angle with change in distance at various latitudes, you can calculate the shape of this spheroid. Newton discussed this phenomenon in Principia and it also gained some theoretical coverage by Arab authors during the Golden Age (though without any actual estimates, just the theory). Pretty good estimates of the shape of the spheroid had been made using astronomical measurements by the 1700s.

in essence trigonometry is really where it could have been realised?

dv said:

Got any refs?

The Rev Dodgson said:

dv said:

Got any refs?

Need only three known points.

roughbarked said:

The Rev Dodgson said:

dv said:

Got any refs?

Need only three known points.

Even kookaburras had that worked out before the pommies called them laughing jackasses.

The Rev Dodgson said:

Got any refs?

Here’s a little something something.

Development of the Ellipsoidal Mode (Penn State college of the Earth and Mineral Sciences)
https://www.e-education.psu.edu/geog862/node/1796

Actually Wikipedia gives a pretty good account so I won’t try to best it. It also provides several primary references.

https://en.wikipedia.org/wiki/History_of_geodesy#Early_modern_period

Jean Picard performed the first modern meridian arc measurement in 1669–1670. He measured a baseline using wooden rods, a telescope (for his angular measurements), and logarithms (for computation). Jacques Cassini later continued Picard’s arc (Paris meridian arc) northward to Dunkirk and southward to the Spanish border. Cassini divided the measured arc into two parts, one northward from Paris, another southward. When he computed the length of a degree from both chains, he found that the length of one degree of latitude in the northern part of the chain was shorter than that in the southern part (see illustration).

This result, if correct, meant that the earth was not a sphere, but a prolate spheroid (taller than wide). However, this contradicted computations by Isaac Newton and Christiaan Huygens. In 1659, Christiaan Huygens was the first to derive the now standard formula for the centripetal force in his work De vi centrifuga. The formula played a central role in classical mechanics and became known as the second of Newton’s laws of motion. Newton’s theory of gravitation combined with the rotation of the Earth predicted the Earth to be an oblate spheroid (wider than tall), with a flattening of 1:230.

The issue could be settled by measuring, for a number of points on earth, the relationship between their distance (in north-south direction) and the angles between their zeniths. On an oblate Earth, the meridional distance corresponding to one degree of latitude will grow toward the poles, as can be demonstrated mathematically.
The French Academy of Sciences dispatched two expeditions. One expedition (1736–37) under Pierre Louis Maupertuis was sent to Torne Valley (near the Earth’s northern pole). The second mission (1735–44) under Pierre Bouguer was sent to what is modern-day Ecuador, near the equator. Their measurements demonstrated an oblate Earth, with a flattening of 1:210. This approximation to the true shape of the Earth became the new reference ellipsoid.

In 1787 the first precise trigonometric survey to be undertaken within Britain was the Anglo-French Survey. Its purpose was to link the Greenwich and Paris’ observatories. The survey is very significant as the forerunner of the work of the Ordnance Survey which was founded in 1791, one year after William Roy’s death.
Between 1792 and 1798 Pierre Méchain and Jean-Baptiste Delambre surveyed the Paris meridian arc between Dunkirk and Barcelona. They extrapolated from this measurement the distance from the North Pole to the Equator which was 5 130 740 toises. As the metre had to be equal to one ten-million of this distance, it was defined as 0,513074 toises or 443,296 lignes of the Toise of Peru (see below).

Actually Wikipedia gives a pretty good account so I won’t try to best it. It also provides several primary references.

https://en.wikipedia.org/wiki/History_of_geodesy#Early_modern_period

Jean Picard performed the first modern meridian arc measurement in 1669–1670. He measured a baseline using wooden rods, a telescope (for his angular measurements), and logarithms (for computation). Jacques Cassini later continued Picard’s arc (Paris meridian arc) northward to Dunkirk and southward to the Spanish border. Cassini divided the measured arc into two parts, one northward from Paris, another southward. When he computed the length of a degree from both chains, he found that the length of one degree of latitude in the northern part of the chain was shorter than that in the southern part (see illustration).

This result, if correct, meant that the earth was not a sphere, but a prolate spheroid (taller than wide). However, this contradicted computations by Isaac Newton and Christiaan Huygens. In 1659, Christiaan Huygens was the first to derive the now standard formula for the centripetal force in his work De vi centrifuga. The formula played a central role in classical mechanics and became known as the second of Newton’s laws of motion. Newton’s theory of gravitation combined with the rotation of the Earth predicted the Earth to be an oblate spheroid (wider than tall), with a flattening of 1:230.

The issue could be settled by measuring, for a number of points on earth, the relationship between their distance (in north-south direction) and the angles between their zeniths. On an oblate Earth, the meridional distance corresponding to one degree of latitude will grow toward the poles, as can be demonstrated mathematically.
The French Academy of Sciences dispatched two expeditions. One expedition (1736–37) under Pierre Louis Maupertuis was sent to Torne Valley (near the Earth’s northern pole). The second mission (1735–44) under Pierre Bouguer was sent to what is modern-day Ecuador, near the equator. Their measurements demonstrated an oblate Earth, with a flattening of 1:210. This approximation to the true shape of the Earth became the new reference ellipsoid.

In 1787 the first precise trigonometric survey to be undertaken within Britain was the Anglo-French Survey. Its purpose was to link the Greenwich and Paris’ observatories. The survey is very significant as the forerunner of the work of the Ordnance Survey which was founded in 1791, one year after William Roy’s death.
Between 1792 and 1798 Pierre Méchain and Jean-Baptiste Delambre surveyed the Paris meridian arc between Dunkirk and Barcelona. They extrapolated from this measurement the distance from the North Pole to the Equator which was 5 130 740 toises. As the metre had to be equal to one ten-million of this distance, it was defined as 0,513074 toises or 443,296 lignes of the Toise of Peru (see below).

Making doubly sure that we got the message?

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

But they didn’t do it in a way that finds the local radius with sufficient accuracy to determine the difference in radius between the equator and the poles, which is what I’m interested in.

there’s the nub.

More specifically, I’m interested in how it was done in the 19th or first half 20th Centuries, or whenever the first reasonably accurate measurements were made.

Father in law was a surveyor prior to WWII. Back then, surveyors had to be skilled in astronomy as well. An error of even one second in time could make a big difference in longitude.

When i went through, narrow steel tape on a roll was used for distance.

Famous early surveys included one of France in 1808. The emporer was not pleased as it showed that France was about 15% smaller than had been thought.

And a famous British survey of India, the great trigonomical survey of 1802 to 1852. The theodolite weighed half a ton.

roughbarked said:

roughbarked said:

The Rev Dodgson said:

Got any refs?

Need only three known points.

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

mollwollfumble said:

The Rev Dodgson said:

roughbarked said:

there’s the nub.

More specifically, I’m interested in how it was done in the 19th or first half 20th Centuries, or whenever the first reasonably accurate measurements were made.

Father in law was a surveyor prior to WWII. Back then, surveyors had to be skilled in astronomy as well. An error of even one second in time could make a big difference in longitude.

When i went through, narrow steel tape on a roll was used for distance.

Famous early surveys included one of France in 1808. The emporer was not pleased as it showed that France was about 15% smaller than had been thought.

And a famous British survey of India, the great trigonomical survey of 1802 to 1852. The theodolite weighed half a ton.

My father in law was a navigator on Sunderlands during the war. He’d graduated to that from starting out at age 14 as a sleeper cutter in what was then, the Big Scrub.

dv said:

The Rev Dodgson said:

Got any refs?

Here’s a little something something.

Development of the Ellipsoidal Mode (Penn State college of the Earth and Mineral Sciences)
https://www.e-education.psu.edu/geog862/node/1796

Thanks.

The Rev Dodgson said:

roughbarked said:

roughbarked said:

Need only three known points.

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances in stereo. Butcherbirds are another easily recognisable species. Triangulating their territorial space.

roughbarked said:

The Rev Dodgson said:

roughbarked said:

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances in stereo. Butcherbirds are another easily recognisable species. Triangulating their territorial space.

Forget stereo. My bad. Think omnidirectional.

The Ancient Greeks knew nothing of kookaburras but perhaps could have used related birds such as the common kingfisher.

dv said:

The Ancient Greeks knew nothing of kookaburras but perhaps could have used related birds such as the common kingfisher.

Indeed. and relating to that the answer the RevD really wants equates to observation. If birds can do it, why not us?

https://www.youtube.com/watch?v=G8cbIWMv0rI

Carl Sagan – Cosmos – Eratosthenes

The Rev Dodgson said:

roughbarked said:

roughbarked said:

Need only three known points.

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You may well scoff, but do that directly at a kookaburra and they’d just laugh at you.

roughbarked said:

The Rev Dodgson said:

roughbarked said:

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances. Butcherbirds are another easily recognisable species.

Never in bush as flat as that. Have to be extremely flat, even just the height of the kooka in the tree would make a world of difference.

The terminator line separating night from day travels at 1,600 km/h.

So what would a five second time difference be? 2.2 km. The kookas would have to be darn accurate.

sibeen said:

The Rev Dodgson said:

roughbarked said:

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You may well scoff, but do that directly at a kookaburra and they’d just laugh at you.

:)

roughbarked said:

The Rev Dodgson said:

roughbarked said:

Even kookaburras had that worked out before the pommies called them laughing jackasses.

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances in stereo. Butcherbirds are another easily recognisable species. Triangulating their territorial space.

So just one of your random comments then, unrelated to the topic of the thread, or am I missing something?

Birds have remarkable navigation abilities, obviously, but I doubt that they have a concept of the Earth being an oblate spheroid.

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

I’m pretty sceptical that kookaburras have even a rough estimate of the radius of the Earth, let alone the difference between the radii at the Poles and Equator.

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances in stereo. Butcherbirds are another easily recognisable species. Triangulating their territorial space.

So just one of your random comments then, unrelated to the topic of the thread, or am I missing something?

Birds have remarkable navigation abilities, obviously, but I doubt that they have a concept of the Earth being an oblate spheroid.

You’re missing something. See my reply earlier.

mollwollfumble said:

The Rev Dodgson said:

Also, any idea why the French thought the Earth would be prolate?

Thanks, my Bingeing didn’t find that.

But it’s still measuring the average radius over a long distance. How can we accurately measure the radius at a point (or a comparatively short distance)?

> why the French thought the Earth would be prolate?

Found it. In a word, Cassini.

“Giovanni Domenico Cassini rejected Newton’s theory of gravity, after measurements (in about 1675) he conducted which wrongly suggested that the Earth was elongated at its poles. More than forty years of controversy about the subject were closed in favour of Newton’s theory after the measurements of the French Geodesic Mission (1736 to 1744) and the Lapponian expedition in 1737 led by Pierre Louis Moreau de Maupertuis”. Cassini probably had access to an astronomer called Jean Richer in French Guiana for information on which to base his calculations.

> How can we accurately measure the radius at a point (or a comparatively short distance)?

Alfred Russel Wallace did that.

In 1870, a Flat-Earth proponent named John Hampden offered a £500 wager in a magazine advertisement to anyone who could demonstrate a convex curvature in a body of water such as a river, canal, or lake. Wallace, intrigued by the challenge and short of money at the time, designed an experiment in which he set up two objects along a six-mile (10 km) stretch of canal. Both objects were at the same height above the water, and he mounted a telescope on a bridge at the same height above the water as well. When seen through the telescope, one object appeared higher than the other, showing the curvature of the earth.

> my Bingeing didn’t find that

I’m going from memory, so may have an anachronism in there. I have a book called “Parallax” about how astronomers failed to, and later succeeded in finding the distances to the nearest stars. I probably remembered it from that.

I’m trying to figure out when Ptolemy’s wrong radius was corrected.

Eratosthenes got it right C100 BC
Others at about the same time got it wrong.
Ptolemy used the wrong radius in his Geography in 150 AD
Columbus was still using the wrong Ptolemy radius in 1502

Tycho by 1588 was collaborating with astronomers in different parts of Europe, but did he have the correct radius of the Earth? Tycho knew the distance to Saturn by 1602 (though not necessarily accurately).

Ah, here we go, https://en.wikipedia.org/wiki/History_of_geodesy

“Around AD 830 Caliph al-Ma’mun commissioned a group of astronomers led by Al-Khwarizmi to measure the distance from Tadmur (Palmyra) to Raqqa” They got the correct radius of the Earth.

“In 1505 the cosmographer and explorer Duarte Pacheco Pereira calculated the value of the degree of the meridian arc with a margin of error of only 4%, when the current error at the time varied between 7 and 15%.”

More on prolate in Paris here, too.

“Jean Picard performed the first modern meridian arc measurement in 1669–1670. He measured a baseline using wooden rods, a telescope … Jacques Cassini later continued Picard’s arc (Paris meridian arc) northward to Dunkirk and southward to the Spanish border. Cassini divided the measured arc into two parts, one northward from Paris, another southward. When he computed the length of a degree from both chains, he found that the length of one degree of latitude in the northern part of the chain was shorter than that in the southern part. This result, if correct, meant that the earth was not a sphere, but a prolate spheroid (taller than wide). However, this contradicted computations by Isaac Newton and Christiaan Huygens.”

Missed this one yesterday.

So by early 18th century survey techniques were sufficiently accurate to measure the variation in radius between tropical regions and northern near Arctic regions, and get the right answer. DV’s link from yesterday (Development of the Ellipsoidal Mode (Penn State college of the Earth and Mineral Sciences) https://www.e-education.psu.edu/geog862/node/1796) also covers that and is well worth a read.

None of the sources say how long the base lines were though (unless I missed it), so lets work it out.

The variation in radius is 22 km from Equator to Poles, but to avoid having to travel to the N Pole lets say our chosen locations have a difference in radius of 10 km, and we are aiming to measure the radius to an accuracy of +-1 km.

Suppose our theodolites have a precision of 1 second, so lets say an error range of +- 5 seconds, or about 0.0014 degrees, or 2.4e-5 radians. An arc of 2.4e-5 radians with radius 6360 km is about 150 m long, so to measure the radius to an accuracy of 1 part in 6000 we would need an arc length of 6000 × 0.15 km = 900 km.

So quite a long “point”.

mollwollfumble said:

The Rev Dodgson said:

roughbarked said:

You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances in stereo. Butcherbirds are another easily recognisable species. Triangulating their territorial space.

So just one of your random comments then, unrelated to the topic of the thread, or am I missing something?

Birds have remarkable navigation abilities, obviously, but I doubt that they have a concept of the Earth being an oblate spheroid.

You’re missing something. See my reply earlier.

I’m still missing it.

Which reply?

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

So just one of your random comments then, unrelated to the topic of the thread, or am I missing something?

Birds have remarkable navigation abilities, obviously, but I doubt that they have a concept of the Earth being an oblate spheroid.

You’re missing something. See my reply earlier.

I’m still missing it.

Which reply?

This one, it was only two posts earlier in the thread, replying to “as the sun comes up the birds sound as if they are coming towards you … kookaburras and butcherbirds”.

> roughbarked said:

> You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances. Butcherbirds are another easily recognisable species.

Never in bush as flat as that. Have to be extremely flat, even just the height of the kooka in the tree would make a world of difference.

The terminator line separating night from day travels at 1,600 km/h. So what would a five second time difference be? 2.2 km. The kookas would have to be darn accurate.

And also, the sound of the kookaburras only travels towards you at 1,235 km/hr, which is less than 1,600 km/hr. Even if kookas at dawn were singing at the exact same time relative to dawn, you would still hear those closer before you heard those further away.

OK, so latitude makes a difference, but not by enough to counter the argument. The sound of kookaburras singing in the morning does not mean that the first ones get to see the sunrise earlier.

mollwollfumble said:

The Rev Dodgson said:

mollwollfumble said:

You’re missing something. See my reply earlier.

I’m still missing it.

Which reply?

This one, it was only two posts earlier in the thread, replying to “as the sun comes up the birds sound as if they are coming towards you … kookaburras and butcherbirds”.

> roughbarked said:

> You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances. Butcherbirds are another easily recognisable species.

Never in bush as flat as that. Have to be extremely flat, even just the height of the kooka in the tree would make a world of difference.

The terminator line separating night from day travels at 1,600 km/h. So what would a five second time difference be? 2.2 km. The kookas would have to be darn accurate.

And also, the sound of the kookaburras only travels towards you at 1,235 km/hr, which is less than 1,600 km/hr. Even if kookas at dawn were singing at the exact same time relative to dawn, you would still hear those closer before you heard those further away.

OK, so latitude makes a difference, but not by enough to counter the argument. The sound of kookaburras singing in the morning does not mean that the first ones get to see the sunrise earlier.

I still don’t see what it has to do with precisely measuring the radius of the Earth.

mollwollfumble said:

The Rev Dodgson said:

mollwollfumble said:

You’re missing something. See my reply earlier.

I’m still missing it.

Which reply?

This one, it was only two posts earlier in the thread, replying to “as the sun comes up the birds sound as if they are coming towards you … kookaburras and butcherbirds”.

> roughbarked said:

> You can be as sceptical as you like and I will never argue along lines that fit the model.
Ever listened to a dawn chorus in the bush? As the sun comes, the birds sound as if they are coming to you.
Birds hear and recall all of this information. Kookaburras and many other birds do but kookaburras are noted for it because they can be heard over such distances. Butcherbirds are another easily recognisable species.

Never in bush as flat as that. Have to be extremely flat, even just the height of the kooka in the tree would make a world of difference.

The terminator line separating night from day travels at 1,600 km/h. So what would a five second time difference be? 2.2 km. The kookas would have to be darn accurate.

And also, the sound of the kookaburras only travels towards you at 1,235 km/hr, which is less than 1,600 km/hr. Even if kookas at dawn were singing at the exact same time relative to dawn, you would still hear those closer before you heard those further away.

OK, so latitude makes a difference, but not by enough to counter the argument. The sound of kookaburras singing in the morning does not mean that the first ones get to see the sunrise earlier.

Although that does give me an idea for measuring the radius of the Earth, approximately. Have three people with guns on flat ground, a long way apart, with synchronised watches. As soon as the Eastmost sees the sunrise, fire off a shot and start the clock. Ditto for the other two. Record when you hear the sound from the other guns. A little maths gives the speed at which the terminator moves and hence the circumference of the Earth.

Ideally, do this twice, once when the first sunlight clears the horizon, then a few minutes later when the last sunlight clears the horizon.

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

The Rev Dodgson said:

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

i think reading this thread some people are digging themselves a hole. a hole to the centre of the Earth. which is handy i guess.

The Rev Dodgson said:

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Nobody said anything about precise. Give or take a few percent would be the best possible for a measurement of the Earth’s radius that takes only one day from start to finish.

Radius = circumference divided by 2 pi.

Adjust for latitude, of course, call it theta. Correct me if I’m wrong, but I think you’ll find that there’s no correction needed for season. The radius of the Earth at the equator (assuming spherical) is obtained by simply dividing the radius at latitude by cos(theta).

mollwollfumble said:

Nobody said anything about precise.

At least one person mentioned precise:

“OK, I knew about Eratosthenes, but if (for instance) you wanted to measure the difference in radius between the Equator and the Poles, how would you do that?”

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

Also, any idea why the French thought the Earth would be prolate?

Thanks, my Bingeing didn’t find that.

But it’s still measuring the average radius over a long distance. How can we accurately measure the radius at a point (or a comparatively short distance)?

> why the French thought the Earth would be prolate?

Found it. In a word, Cassini.

“Giovanni Domenico Cassini rejected Newton’s theory of gravity, after measurements (in about 1675) he conducted which wrongly suggested that the Earth was elongated at its poles. More than forty years of controversy about the subject were closed in favour of Newton’s theory after the measurements of the French Geodesic Mission (1736 to 1744) and the Lapponian expedition in 1737 led by Pierre Louis Moreau de Maupertuis”. Cassini probably had access to an astronomer called Jean Richer in French Guiana for information on which to base his calculations.

> How can we accurately measure the radius at a point (or a comparatively short distance)?

Alfred Russel Wallace did that.

In 1870, a Flat-Earth proponent named John Hampden offered a £500 wager in a magazine advertisement to anyone who could demonstrate a convex curvature in a body of water such as a river, canal, or lake. Wallace, intrigued by the challenge and short of money at the time, designed an experiment in which he set up two objects along a six-mile (10 km) stretch of canal. Both objects were at the same height above the water, and he mounted a telescope on a bridge at the same height above the water as well. When seen through the telescope, one object appeared higher than the other, showing the curvature of the earth.

> my Bingeing didn’t find that

I’m going from memory, so may have an anachronism in there. I have a book called “Parallax” about how astronomers failed to, and later succeeded in finding the distances to the nearest stars. I probably remembered it from that.

I’m trying to figure out when Ptolemy’s wrong radius was corrected.

Eratosthenes got it right C100 BC
Others at about the same time got it wrong.
Ptolemy used the wrong radius in his Geography in 150 AD
Columbus was still using the wrong Ptolemy radius in 1502

Tycho by 1588 was collaborating with astronomers in different parts of Europe, but did he have the correct radius of the Earth? Tycho knew the distance to Saturn by 1602 (though not necessarily accurately).

Ah, here we go, https://en.wikipedia.org/wiki/History_of_geodesy

“Around AD 830 Caliph al-Ma’mun commissioned a group of astronomers led by Al-Khwarizmi to measure the distance from Tadmur (Palmyra) to Raqqa” They got the correct radius of the Earth.

“In 1505 the cosmographer and explorer Duarte Pacheco Pereira calculated the value of the degree of the meridian arc with a margin of error of only 4%, when the current error at the time varied between 7 and 15%.”

More on prolate in Paris here, too.

“Jean Picard performed the first modern meridian arc measurement in 1669–1670. He measured a baseline using wooden rods, a telescope … Jacques Cassini later continued Picard’s arc (Paris meridian arc) northward to Dunkirk and southward to the Spanish border. Cassini divided the measured arc into two parts, one northward from Paris, another southward. When he computed the length of a degree from both chains, he found that the length of one degree of latitude in the northern part of the chain was shorter than that in the southern part. This result, if correct, meant that the earth was not a sphere, but a prolate spheroid (taller than wide). However, this contradicted computations by Isaac Newton and Christiaan Huygens.”

Missed this one yesterday.

So by early 18th century survey techniques were sufficiently accurate to measure the variation in radius between tropical regions and northern near Arctic regions, and get the right answer. DV’s link from yesterday (Development of the Ellipsoidal Mode (Penn State college of the Earth and Mineral Sciences) https://www.e-education.psu.edu/geog862/node/1796) also covers that and is well worth a read.

None of the sources say how long the base lines were though (unless I missed it), so lets work it out.

The variation in radius is 22 km from Equator to Poles, but to avoid having to travel to the N Pole lets say our chosen locations have a difference in radius of 10 km, and we are aiming to measure the radius to an accuracy of +-1 km.

Suppose our theodolites have a precision of 1 second, so lets say an error range of +- 5 seconds, or about 0.0014 degrees, or 2.4e-5 radians. An arc of 2.4e-5 radians with radius 6360 km is about 150 m long, so to measure the radius to an accuracy of 1 part in 6000 we would need an arc length of 6000 × 0.15 km = 900 km.

So quite a long “point”.

If your point is that the precision with which the shape of the earth was greatly improved with the advent of satellite technology, then you are correct.

Note though that you’ve somewhat misrepresented the uncertainty in pre-satellite methods. It doesn’t matter that the baselines were long. From our knowledge of gravity we expect the shape of the spheroid to be simply parameterisable, and with enough measurements you can very accurately determine those parameters. You don’t need to perform a specific calculation for your location: just generate the model for the shape of the spheroid, look your latitude up in the table. Even before satellites, the model was good enough to give you an answer for your specific latitude that had less than 0.1% uncertainty.

Now of course it’s less than 0.0001% uncertainty…

Still, if you wanted to get very high precision without satellite tech, for some reason, with modern laser interferometry you could establish a line of sight grid on land.

The Rev Dodgson said:

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

dv said:

The Rev Dodgson said:

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

Kookaburras: Ha Ha Ha.

dv said:

The Rev Dodgson said:

mollwollfumble said:

> I still don’t see what it has to do with precisely measuring the radius of the Earth.

24 (hrs) * the speed of the terminator (km/hr) = the circumference of the Earth (km).

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

kakakakakakaka

Cymek said:

The Rev Dodgson said:

dv said:

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

kakakakakakaka

OK, that’s not too difficult.

How do you interpret their response?

The Rev Dodgson said:

Cymek said:

The Rev Dodgson said:

How do you get the kookaburras to tell you what the latitude is?

kakakakakakaka

OK, that’s not too difficult.

How do you interpret their response?

Inaccurately

Cymek said:

The Rev Dodgson said:

Cymek said:

kakakakakakaka

OK, that’s not too difficult.

How do you interpret their response?

Inaccurately

That’s what I feared.

We could adapt the kookaburra method though:

Find a large island with a mountain in the middle, that allows a direct line of sight to the East and West coast. Get someone to stand at each coast line and signal when they see the sun rise, and measure the time between the two signals.

You then just need an accurate measurement of the distance, and the latitude, and you have your answer.

I might suggest another experiment. Build a tall tower on the coast. Rig a ship or boat with a tall mast and sails painted in various colours in horizontal bands. Have some kind measuring rope on buoys (a few km long) attaching boat to shore. When there is a favourable wind or current let the boat drift out until the measuring line rope becomes taut. Then have an observer on the ground and one in the tower record which colour stripe on the sail they can see. All of these heights and the length of the measuring rope should be known, so from that we should be able to work out the rest.

party_pants said:

Rig a ship or boat with a tall mast and sails painted in various colours in horizontal bands.

sounds very gay.

ChrispenEvan said:

party_pants said:

Rig a ship or boat with a tall mast and sails painted in various colours in horizontal bands.

sounds very gay.

You could just do black and white stripes (or even dark blue) if you prefer, and have the observers count the number of stripes they see.

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

I could teach a cockatoo to do that.

mollwollfumble said:

The Rev Dodgson said:

dv said:

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

I could teach a cockatoo to do that.

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

How do you get the kookaburras to tell you what the latitude is?

I could teach a cockatoo to do that.

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

mollwollfumble said:

The Rev Dodgson said:

mollwollfumble said:

I could teach a cockatoo to do that.

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

I imagine there is some arbitrary circle defined for the equator, so that the average distance from the circle to mean seal level is minimised, then the angle of latitude is defined by the line connecting a point to the centre of the circle.

But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

So how do people define horizontal when they are measuring the elevation of astronomical objects?

The Rev Dodgson said:

So how do people define horizontal when they are measuring the elevation of astronomical objects?

local horizon i believe.

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

Yes I know that, but what does that have to do with precisely measuring the radius of the Earth?

Apart from which it gives you the radius to the axis of rotation, not to the centre.

Far be it from me to defend the kookaburra method but if you have a function of “distance to axis of rotation versus latitude” function then with a bit of nous you should be able to turn that into a “distance to the centre of the earth versus latitude” function.

How do you get the kookaburras to tell you what the latitude is?

Gay your life must be

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

How do you get the kookaburras to tell you what the latitude is?

I could teach a cockatoo to do that.

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

Altitude of the celestial pole

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

I imagine there is some arbitrary circle defined for the equator, so that the average distance from the circle to mean seal level is minimised, then the angle of latitude is defined by the line connecting a point to the centre of the circle.

But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

So how do people define horizontal when they are measuring the elevation of astronomical objects?

> But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

Yes! I struck that earlier, when i was looking at from the point of view of reference height for antarctic mountains. I wanted to know how “sea level” was defined at the south pole. I’d forgotten it until now.

GPS heights are all based on the WGS 84 reference ellipsoid.

Defining Parameters

The coordinate origin of WGS 84 is meant to be located at the Earth’s center of mass; the uncertainty is believed to be less than 2 cm.

The WGS 84 meridian of zero longitude is the IERS Reference Meridian, 5.3 arc seconds or 102 metres (335 ft) east of the Greenwich meridian at the latitude of the Royal Observatory.

The WGS 84 datum surface is an oblate spheroid with equatorial radius a = 6378137 m at the equator and flattening f = 1/298.257223563. The refined value of the WGS 84 gravitational constant (mass of Earth’s atmosphere included) is GM = 3986004.418×108 m³/s². The angular velocity of the Earth is defined to be ω = 72.92115×10−6 rad/s.

This leads to several computed parameters such as the polar semi-minor axis b which equals a × (1 − f) = 6356752.3142 m, and the first eccentricity squared, e² = 6.69437999014×10−3.

Currently, WGS 84 uses the Earth Gravitational Model 2008. This geoid defines the nominal sea level surface by means of a spherical harmonics series of degree 360 (which provides about 100 km latitudinal resolution near the Equator). The deviations of the EGM96 geoid from the WGS 84 reference ellipsoid range from about −105 m to about +85 m. EGM96 differs from the original WGS 84 geoid, referred to as EGM84.

To lose weight, stay away from red areas such as Britain and Europe and head for blue areas such as Perth and Sri Lanka.

The Rev Dodgson said:

mollwollfumble said:

The Rev Dodgson said:

I hope you wouldn’t cheat by giving the cockatoo the number.

How is the angle of latitude defined anyway?

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

I imagine there is some arbitrary circle defined for the equator, so that the average distance from the circle to mean seal level is minimised, then the angle of latitude is defined by the line connecting a point to the centre of the circle.

But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

So how do people define horizontal when they are measuring the elevation of astronomical objects?

On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular (or normal) to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes which are used in special applications.

Geodetic and geocentric latitudes
Edit

The definition of geodetic latitude (φ) and longitude (λ) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.
The graticule on the ellipsoid is constructed in exactly the same way as on the sphere. The normal at a point on the surface of an ellipsoid does not pass through the centre, except for points on the equator or at the poles, but the definition of latitude remains unchanged as the angle between the normal and the equatorial plane. The terminology for latitude must be made more precise by distinguishing:

Geodetic latitude: the angle between the normal and the equatorial plane. The standard notation in English publications is φ. This is the definition assumed when the word latitude is used without qualification. The definition must be accompanied with a specification of the ellipsoid.

Geocentric latitude: the angle between the radius (from centre to the point on the surface) and the equatorial plane. (Figure below).
There is no standard notation: examples from various texts include θ, ψ, q, φ′, φc, φg. This article uses θ.

Spherical latitude: the angle between the normal to a spherical reference surface and the equatorial plane.

Geographic latitude must be used with care. Some authors use it as a synonym for geodetic latitude whilst others use it as an alternative to the astronomical latitude.

Latitude (unqualified) should normally refer to the geodetic latitude.

So, with geodetic latitude, the sea level is horizontal to a first approximation, ie on the ellipsoid, which means that the zenith line does not pass through the centre of the Earth.

mollwollfumble said:

The Rev Dodgson said:

mollwollfumble said:

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

I imagine there is some arbitrary circle defined for the equator, so that the average distance from the circle to mean seal level is minimised, then the angle of latitude is defined by the line connecting a point to the centre of the circle.

But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

So how do people define horizontal when they are measuring the elevation of astronomical objects?

On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular (or normal) to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes which are used in special applications.

Geodetic and geocentric latitudes
Edit

The definition of geodetic latitude (φ) and longitude (λ) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.
The graticule on the ellipsoid is constructed in exactly the same way as on the sphere. The normal at a point on the surface of an ellipsoid does not pass through the centre, except for points on the equator or at the poles, but the definition of latitude remains unchanged as the angle between the normal and the equatorial plane. The terminology for latitude must be made more precise by distinguishing:

Geodetic latitude: the angle between the normal and the equatorial plane. The standard notation in English publications is φ. This is the definition assumed when the word latitude is used without qualification. The definition must be accompanied with a specification of the ellipsoid.

Geocentric latitude: the angle between the radius (from centre to the point on the surface) and the equatorial plane. (Figure below).
There is no standard notation: examples from various texts include θ, ψ, q, φ′, φc, φg. This article uses θ.

Spherical latitude: the angle between the normal to a spherical reference surface and the equatorial plane.

Geographic latitude must be used with care. Some authors use it as a synonym for geodetic latitude whilst others use it as an alternative to the astronomical latitude.

Latitude (unqualified) should normally refer to the geodetic latitude.

So, with geodetic latitude, the sea level is horizontal to a first approximation, ie on the ellipsoid, which means that the zenith line does not pass through the centre of the Earth.

Interesting, thanks for that.

mollwollfumble said:

The Rev Dodgson said:

mollwollfumble said:

It’s 23 and a half degrees at the tropics. What sort of question is that?

I suppose it’s not obvious. For example an equator defined as half way between the poles isn’t exactly accurate because the poles wobble a bit. And an equator couldn’t be defined as the greatest circumference, that would be way out. Perhaps it’s defined using the stars.

I imagine there is some arbitrary circle defined for the equator, so that the average distance from the circle to mean seal level is minimised, then the angle of latitude is defined by the line connecting a point to the centre of the circle.

But that means in general the horizontal surface plane at any point is not perpendicular to the radial line defining the latitude; which had not occurred to me before.

So how do people define horizontal when they are measuring the elevation of astronomical objects?

On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular (or normal) to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes which are used in special applications.

Geodetic and geocentric latitudes
Edit

The definition of geodetic latitude (φ) and longitude (λ) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.
The graticule on the ellipsoid is constructed in exactly the same way as on the sphere. The normal at a point on the surface of an ellipsoid does not pass through the centre, except for points on the equator or at the poles, but the definition of latitude remains unchanged as the angle between the normal and the equatorial plane. The terminology for latitude must be made more precise by distinguishing:

Geodetic latitude: the angle between the normal and the equatorial plane. The standard notation in English publications is φ. This is the definition assumed when the word latitude is used without qualification. The definition must be accompanied with a specification of the ellipsoid.

Geocentric latitude: the angle between the radius (from centre to the point on the surface) and the equatorial plane. (Figure below).
There is no standard notation: examples from various texts include θ, ψ, q, φ′, φc, φg. This article uses θ.

Spherical latitude: the angle between the normal to a spherical reference surface and the equatorial plane.

Geographic latitude must be used with care. Some authors use it as a synonym for geodetic latitude whilst others use it as an alternative to the astronomical latitude.

Latitude (unqualified) should normally refer to the geodetic latitude.

So, with geodetic latitude, the sea level is horizontal to a first approximation, ie on the ellipsoid, which means that the zenith line does not pass through the centre of the Earth.

Pick your own arbitrary system.. there is no centre of the earth.

There is no centre of the Earth, there is no centre of the universe, there no centre of the deep-fried ice cream ball.

The Rev’s valiant attempt to measure the radius of the Earth is ultimately futile.

Ian said:

There is no centre of the Earth, there is no centre of the universe, there no centre of the deep-fried ice cream ball.

The Rev’s valiant attempt to measure the radius of the Earth is ultimately futile.

The universe may or may not have a centre.

The other two have quite a few centres, depending on how you choose to define them.

So we all good here?

dv said:

So we all good here?

I am. dunno about the others here. bit dodgy some of them.

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

I think you’d also need a camera.

roughbarked said:

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

I think you’d also need a camera.

http://www.engineeringsurveyor.com/software/Leica_Viva_TS11_TS15_User_Manual.pdf
http://kumonos.info/downloads/datasheet_ts11.pdf

roughbarked said:

roughbarked said:

The Rev Dodgson said:

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

I think you’d also need a camera.

http://www.engineeringsurveyor.com/software/Leica_Viva_TS11_TS15_User_Manual.pdf
http://kumonos.info/downloads/datasheet_ts11.pdf

https://leica-geosystems.com/products/total-stations/robotic-total-stations/leica-viva-ts16

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

And drones. No-one has used drones yet.

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

Okay, so you set up a large line of sight triangular grid of paired laser interferometry stations across the globe. These can measure great distances to accuracies of around a centimetre. I haven’t worked out how many you’d need, it would depend on how many hills there are and how high they are … but certainly it would have to be several hundred or thousands.

Once you know the distances between the elements in such a network you can work out their exact relative locations in 3D space: there will only be one possible configuration. It might be an irreducible problem for pure trigonometry but you can solve it using computational methods.

dv said:

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

Okay, so you set up a large line of sight triangular grid of paired laser interferometry stations across the globe. These can measure great distances to accuracies of around a centimetre. I haven’t worked out how many you’d need, it would depend on how many hills there are and how high they are … but certainly it would have to be several hundred or thousands.

Once you know the distances between the elements in such a network you can work out their exact relative locations in 3D space: there will only be one possible configuration. It might be an irreducible problem for pure trigonometry but you can solve it using computational methods.

Sounds good.

Presumably you would only need a single band of triangles, rather than covering the whole globe.

Can’t you do much better than cm accuracy though? Isn’t this the system the gravity wave detectors use?

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

Okay, so you set up a large line of sight triangular grid of paired laser interferometry stations across the globe. These can measure great distances to accuracies of around a centimetre. I haven’t worked out how many you’d need, it would depend on how many hills there are and how high they are … but certainly it would have to be several hundred or thousands.

Once you know the distances between the elements in such a network you can work out their exact relative locations in 3D space: there will only be one possible configuration. It might be an irreducible problem for pure trigonometry but you can solve it using computational methods.

Sounds good.

Presumably you would only need a single band of triangles, rather than covering the whole globe.

Can’t you do much better than cm accuracy though? Isn’t this the system the gravity wave detectors use?

It’s possible I’m a bit out of date. The ground baedinterferometers used to track tectonism back in the 1990s were good to within a few mm.

You could do it with a belt of triangles but my gut tells me that the accuracy would be greatly improved by including at least a couple of paths.

dv said:

The Rev Dodgson said:

dv said:

Okay, so you set up a large line of sight triangular grid of paired laser interferometry stations across the globe. These can measure great distances to accuracies of around a centimetre. I haven’t worked out how many you’d need, it would depend on how many hills there are and how high they are … but certainly it would have to be several hundred or thousands.

Once you know the distances between the elements in such a network you can work out their exact relative locations in 3D space: there will only be one possible configuration. It might be an irreducible problem for pure trigonometry but you can solve it using computational methods.

Sounds good.

Presumably you would only need a single band of triangles, rather than covering the whole globe.

Can’t you do much better than cm accuracy though? Isn’t this the system the gravity wave detectors use?

It’s possible I’m a bit out of date. The ground baedinterferometers used to track tectonism back in the 1990s were good to within a few mm.

You could do it with a belt of triangles but my gut tells me that the accuracy would be greatly improved by including at least a couple of paths.

I think making the “belts” as thick as possible (by using alternating sea level and mountain top nodes) would also help.

I might set up a spreadsheet for it, when I have time.

dv said:

The Rev Dodgson said:

dv said:

So we all good here?

I’m sure there must still be matters undiscussed.

For instance, how you go about measuring the radius with lasers?

Okay, so you set up a large line of sight triangular grid of paired laser interferometry stations across the globe. These can measure great distances to accuracies of around a centimetre. I haven’t worked out how many you’d need, it would depend on how many hills there are and how high they are … but certainly it would have to be several hundred or thousands.

Once you know the distances between the elements in such a network you can work out their exact relative locations in 3D space: there will only be one possible configuration. It might be an irreducible problem for pure trigonometry but you can solve it using computational methods.

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

Sounds good.

Presumably you would only need a single band of triangles, rather than covering the whole globe.

Can’t you do much better than cm accuracy though? Isn’t this the system the gravity wave detectors use?

It’s possible I’m a bit out of date. The ground baedinterferometers used to track tectonism back in the 1990s were good to within a few mm.

You could do it with a belt of triangles but my gut tells me that the accuracy would be greatly improved by including at least a couple of paths.

I think making the “belts” as thick as possible (by using alternating sea level and mountain top nodes) would also help.

I might set up a spreadsheet for it, when I have time.

This is without satellites, i take it.

I’m not understanding what you mean by “paired interferometers”. How big an interferometer station at each end are you talking about, breadbox size, tabletop size, building size or km size?

Why not use ordinary portable surveying tools such as a top of the range theodolite with laser ranging, or are you?

PS, astrometry, the accurate determination of star positions, is so difficult that telescopes on Earth gave up trying to do it more than a hundred years ago (iiuc). Relying instead on tables to know where to point.

mollwollfumble said:

dv said:

The Rev Dodgson said:

It’s possible I’m a bit out of date. The ground baedinterferometers used to track tectonism back in the 1990s were good to within a few mm.

You could do it with a belt of triangles but my gut tells me that the accuracy would be greatly improved by including at least a couple of paths.

I think making the “belts” as thick as possible (by using alternating sea level and mountain top nodes) would also help.

I might set up a spreadsheet for it, when I have time.

This is without satellites, i take it.

I’m not understanding what you mean by “paired interferometers”. How big an interferometer station at each end are you talking about, breadbox size, tabletop size, building size or km size?

Why not use ordinary portable surveying tools such as a top of the range theodolite with laser ranging, or are you?

PS, astrometry, the accurate determination of star positions, is so difficult that telescopes on Earth gave up trying to do it more than a hundred years ago (iiuc). Relying instead on tables to know where to point.

OK, i exaggerate. The USNO astrometric 0.2 metre telescope (the tiny one) was set up in 1985.

But star position has been done in much the same way. By triangulation. Atmospheric refraction gets in the way, so stars can only be accurately located relative to one another if they’re in the same patch of sky. A bit like how triangulation has to be done for ground-based surveying on Earth. Once a geodesic dome-like framework is set up, the gaps between the guide stars are filled in.