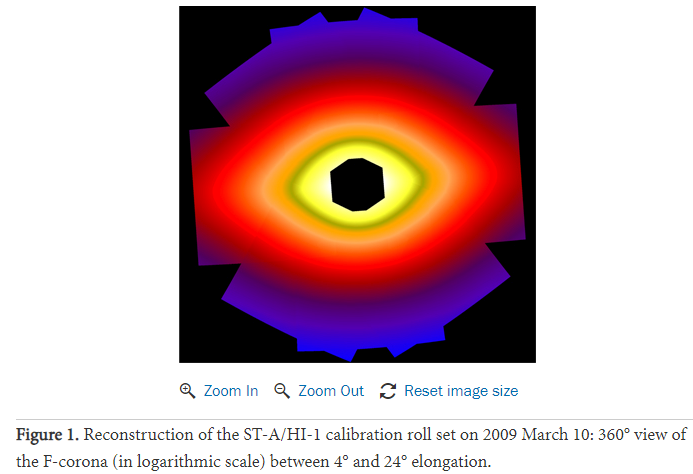
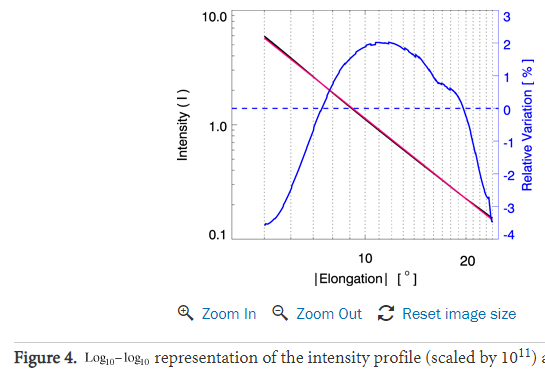
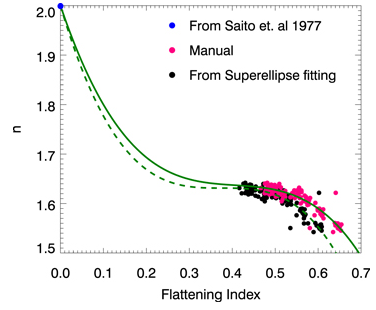
I was going to ask if you knew of any badly aimed videos taken from space or suborbital (eg high altitude balloon or sounding rocket.

The video has to be badly aimed because i need the Sun to drift in or out of frame.

The purpose is to map the brightness of the zodiacal light within 30 degrees of the Sun.

But i may be able to do better.

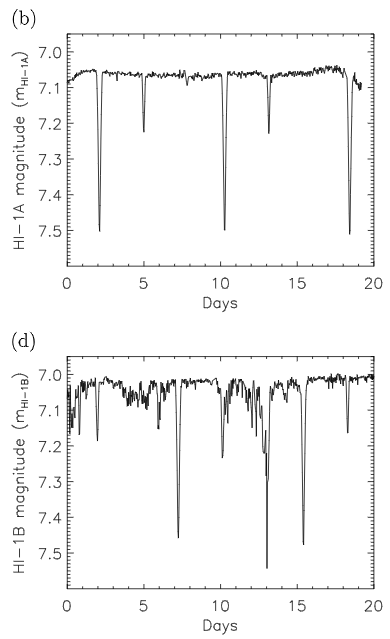
“The STEREO mission (16), launched in October 2006, uses two nearly identical
spacecraft, A and B, to provide synoptic observations of the Sun and the heliosphere interior to
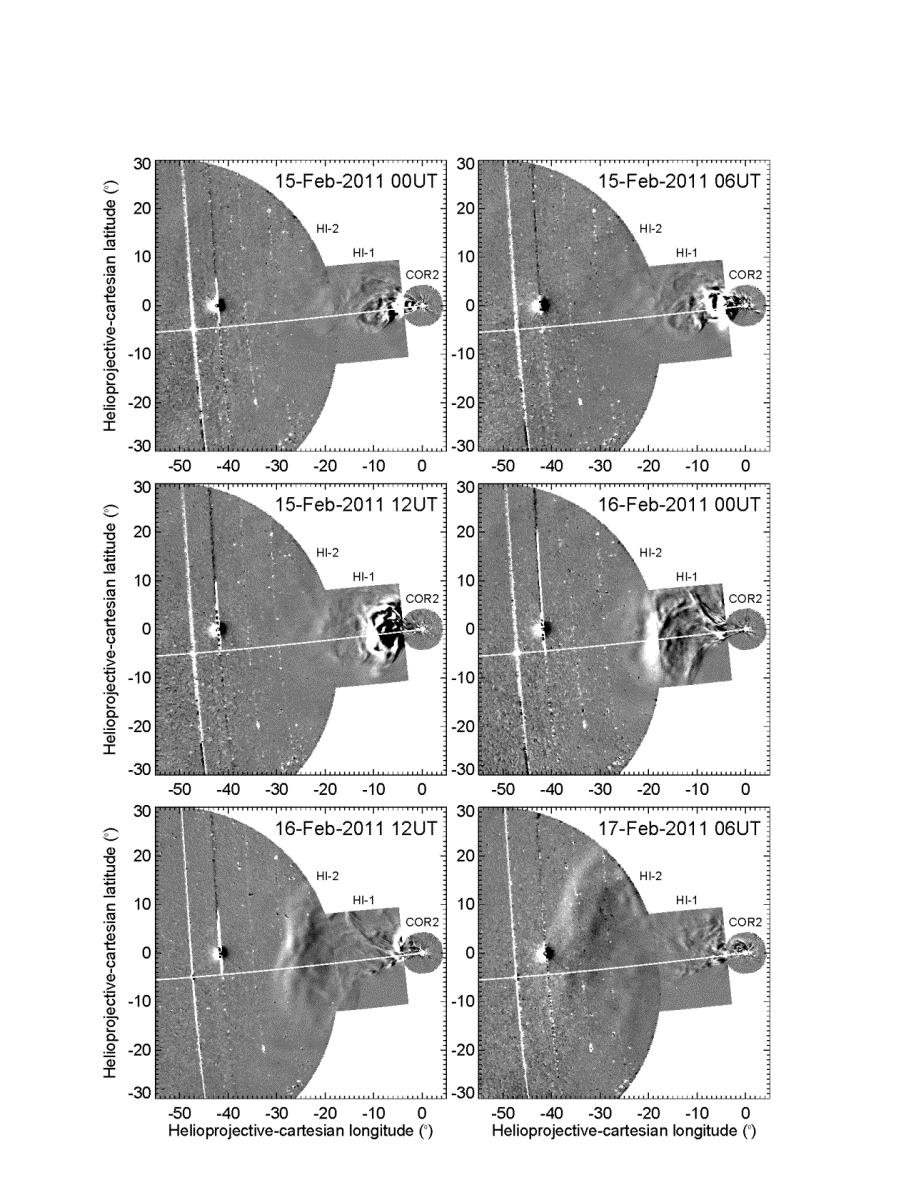
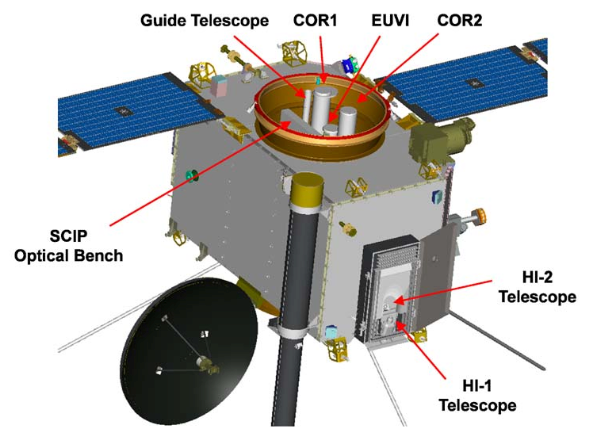
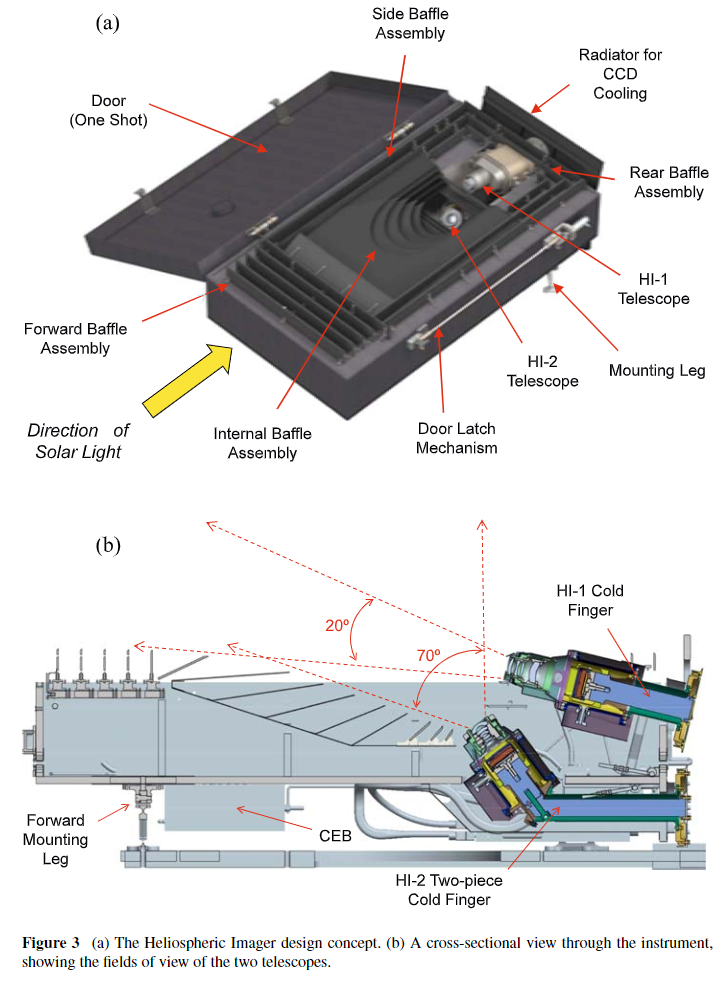
1 AU. Each spacecraft carries a Heliospheric Imager instrument (17), HI-2, both of which
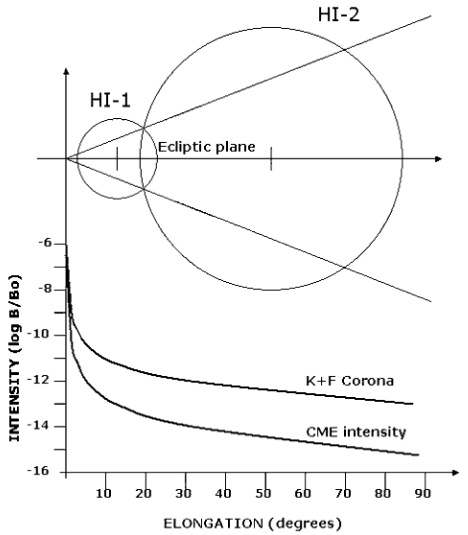
continuously monitor the inner zodiacal cloud. These HI-2A and HI-2B instruments have a field-
of-view of about 70° centred on ecliptic latitude ≈0° at helioecliptic longitude |’|=53.7°. In
searching for a dust ring at the orbit of Venus, the lines-of-sight that are of interest are close to
the ecliptic plane and have 40°<|’|<50° (depending on the location of the spacecraft) (Fig. 1).
In normal science operations, the HI-2 instrument generates a 1024×1024 pixel image
with ≈4 arcmin resolution every two hours. Further processing, including positional calibration
(18), results in the Level-1 data used here. The instrument is sensitive to wavelengths of 400–
1000 nm, and the dominant diffuse source in HI-2 images is solar radiation scattered by dust
grains (with radii 10−100 m (19)) in the zodiacal cloud. The typical surface brightness at
(’≈45°, ≈0°) is ≈8 DN s-1
pixel-1
(DN is data number, 1 DN ≅ 15 photoelectrons is the default
unit used by the instrument team (17)). The HI-2 instrument was designed (17) to monitor
coronal mass ejections having a surface brightness of about 1% of that of the zodiacal light. By
combining ~100 HI-2 Level-1 images, photometry on the zodiacal cloud to an accuracy of order
0.1% can be extracted. A major limitation is the presence of systematic errors that compromise
this photometry. These arise from various sources: saturation stripes, ghosting caused by bright
objects and the presence of the galactic plane within 30° of the region of interest. To avoid
contamination, data containing these features were not used in our analysis.”

From Jones, M. H., Bewsher, D. & Brown, D. S. 2013, Science, 342, 960 “Imaging of a circumsolar dust ring near the orbit of Venus”.

To use that, i’d have to get access to raw data from the HI-2 instrument(s) onboard STEREO.

On the other hand, 53.7 degrees minus 70/2 = 35 degrees is 18.5 degrees, nowhere near close enough to the Sun. I want as close as 5 degrees ideally, 9 degrees worst acceptable.

So i do need badly aimed videos taken from space or suborbital. Please?

There is this suborbital flight, but better optics would be a help. The balloon acts as a coronascope.

Got a better one?

Try checking the various astrology websites they are into the Zodiacs in a big way

Cymek said:

Try checking the various astrology websites they are into the Zodiacs in a big way

I was about to say “no” but they do say “the sun is in” whatever constellation. Which is exactly what i’m trying to photograph. How do you photograph the Sun in Sagittarius? The zodiacal light gets in the way.

That’s why I’m asking for videos taken in space with the Sun in (or a whisker out of) the frame.

Aha.

http://www.stereo.rl.ac.uk

So HI-1, HI-2 and COR2 together image the area i’m interested in.

How?

This image shows a CME propogating from the Sun to the Earth.

Seems as though any number of normal reference works would be better for this purpose

dv said:

Seems as though any number of normal reference works would be better for this purpose

Fingers crossed.

I hadn’t realised that SECCHI onboard STEREO was not one camera, but 5.

“Mounted on the sides of two widely separated spacecraft, the two Heliospheric Imager (HI) instruments onboard NASA’s STEREO mission view, for the first time, the space between the Sun and Earth. These instruments are wide-angle visible-light imagers that incorporate sufficient baffling to eliminate scattered light to the extent that the passage of solar coronal mass ejections (CMEs) through the heliosphere can be detected. Each HI instrument comprises two cameras, HI-1 and HI-2, which have 20° and 70° fields of view and are off-pointed from the Sun direction by 14.0° and 53.7°, respectively, with their optical axes aligned in the ecliptic plane. This arrangement provides coverage over solar elongation angles from 4.0° to 88.7° at the viewpoints of the two spacecraft”.

mollwollfumble’s blind spot telestcope is looking for about 5° to 60°, so is covered, but HI was only used for CME observations, not other transients, and not steady state zodiacal light observations, except as a background to subtract.

By the way, I’m absolutely stunned by the 70° field of view, I had thought the biggest in a space telescope was 27° field of view, and count even 12° as huge.

“a pair of traditional white-light Lyot coronagraphs (COR-1 and COR-2), which cover the coronal regions 1.4R☼–4R☼and 2.5R☼–15R☼.”

“stellar variability studies, including the search for exoplanets; the HI cameras are able to continuously monitor the light-curves of stars down to 12th magnitude from a very stable environment, for periods up to 20 and 70 days for HI-1 and HI-2, respectively”

Well that sure wasn’t in the advertising blurb, but mollwollfumble’s blind spot telescope is aiming for magnitude 24, or at the very least magnitude 20.

Well that is weird, HI-1 and HI-2 don’t seem to be protected at all, just hung off the side off the craft.

“Thomson-scattered photospheric light from free electrons in the solar wind plasma.”

That’s not the same as zodiacal light. Let’s hope it’s part of the same continuum.

“The heritage for the HI instrument comes from the SMEI instrument (Eyles et al.,2003;Jackson et al.,2004), operating aboard the Coriolis spacecraft, launched in 2003. The SMEI instrument is also a wide-angle heliospheric imaging system, with three 60°×3° field-of-view baffled camera systems. The spacecraft is in a Sun-synchronous polar orbit, with its attitude stabilised with respect to the local vertical. The cameras sweep around the sky as the spacecraft orbits the Earth and consequently almost the entire sky is mapped each orbit.”

Shit. That’s practically identical to mollwollfumble’s blind spot telescope. I’ve never heard of the spacecraft “Coriolis”. Have you? Wish i’d found out about it before submitting to ESA, I feel silly now.

“The HI detectors are CCDs with 2048×2048 pixels, where each pixel has a size of 13.5×13.5 μm. These are usually binned onboard to 1024×1024 bins, resulting in image bin angular sizes of 70 arc-sec and 4 arc-min, for HI-1 and HI-2, respectively. Short exposures are taken and cleaned of cosmic rays onboard, and a number of such exposures are then summed to produce an image to be down-linked”.

Now that’s what I call a weird looking telescope. Talk about innovative!

What’s the diameter? It can’t be very big.

“the readout time of each exposure is 4.8 seconds”. Hmm, borderline.

Pixel size 35 arcsec. I’m aiming for 0.7 to 1.4 arcsec, much finer. Only 1 megapixel per camera.

Aha, here’s the inner zodiacal light I was looking for, unfortunately only along the ecliptic, but that’s where it’s strongest.

Got a reference for that. Socker, D.G., Howard, R.A., Korendyke, C.M., Simnett, G.M., Webb, D.F.: 2000, Proc. SPIE 4139, 284.

So, the Coriolis spacecraft (also called Windsat) only has solar observations as a minor part. The major part is observing the Earth’s winds. The space observation part is called SMEI.

http://smei.ucsd.edu/

Not much info on the web. The wikipedia article is only a stub, and even that concentrates on the wind observation part.

“SMEI launched on January 6th, 2003 into an Earth-terminator, Sun synchronous, 840 km polar orbit”.

The following is a slice from a 3-D reconstruction of a coronal mass ejection (CME) from SMEI using tomography! But what interests me is the 3-D background that had to be subtracted to get the CME.

Using three cameras, the whole of the cosmos is imaged every orbit – about 100 minutes. That’s faster than anything else I’m aware of, by a factor of more ten! The baffles around each camera make it look like an equilateral triangle.

Here’s a comet from SMEI

Here’s an image showing zodiacal light (horizontal) and milky way from a single orbit

Image pairs from successive orbits are used to subtract off the background. So it doesn’t need to know the brightness of the Zodiacal light. :-( I’m not sure if the zodiacal light is so bright that it saturates the camera sensor.

Here’s a light curve from a variable star measured by SMEI. For a satellite dedicated to measuring Earth’s wind speeds, that’s impressive.

Below right is a 3-D tomographic image (below right) from the data above and left of it of a CME.

I can actually get real data from SMEI onboard the Coriolis Spacecraft. if I can extract it from a .png file. :-(

The trick would be to run http://smei.ucsd.edu/new_smei/sky/sky_custom.php?orbit=45231
with and without zodiacal light. The difference is the zodiacal light. Equirectangular map. Logarithmic scale.

then subtract off

Why it fails. Even that doesn’t get close enough to the Sun. I’m not sure why. The C3 camera is supposed to get really close to the Sun. It doesn’t get closer than 15 degrees. Which is a good start, but not good enough.

The brightest part of the zodiacal light is brighter than the brightest part of the Milky Way. So perhaps Neutrino’s suggestion of a Lagrangian point is better after all.

mollwollfumble said:

Aha.

http://www.stereo.rl.ac.uk

So HI-1, HI-2 and COR2 together image the area i’m interested in.

How?

This image shows a CME propogating from the Sun to the Earth.

Well, here’s today’s HI-1 image. This is the exact range that I’m most interested in, from 4 degrees out.

Looks like they’ve had fun pre-subtracting off the zodiacal light already, which is why the left side of the image is so smoothed. It looks as if the zodiacal light in the left hand part of the region really stops distant objects, white dots, from being seen.

You can see background objects of interest moving in this three frame mpg posted on the web today.

https://stereo-ssc.nascom.nasa.gov/browse/2019/10/04/ahead_20191004_hi1_512.mpg

mollwollfumble said:

Aha.

http://www.stereo.rl.ac.uk

So HI-1, HI-2 and COR2 together image the area i’m interested in.

How?

This image shows a CME propagating from the Sun to the Earth.

Tracking down references from http://www.stereo.rl.ac.uk/Documents/InstrumentPapers.html

Instrument details in https://rd.springer.com/content/pdf/10.1007%2Fs11214-008-9341-4.pdf so there should be a camera diameter for HI-1 and HI-2 in there somewhere.

Starts with extreme UV instrument.

COR-1 inner coronagraph – 1.4 to 4 Rsun – Pixel 3.75 arcsec – Diameter ? ustated, damn them, but approximately 33 mm.
Looking elsewhere, 36 mm diameter.

COR-2 outer coronagraph – FOV half angle 4 degrees – Pixel 15 arcsec – Diameter ? also ustated, damn them to hell.

Have to go elsewhere for diameter https://www.wmo-sat.info/oscar/instruments/view/846 COR-2 diameter 30.5 mm.

HI-1 diameter 16 mm.

HI-2 diameter 21 mm.

No wonder they can only see stars down to about magnitude 12, given telescope diameters that small. That’s smaller than the average 35 mm camera.

Next paper. https://link.springer.com/article/10.1007/s11207-010-9582-8. Access via sci-hub.

“This is done by analysing the variation in intensity of stars in the background starfield as they pass across the CCD”

Excellent. I hope.

“Thernisienet al.(2006) used ∼60 background stars observed in each filter by SOHO/LASCO-C3 to determine the photometric calibration of SOHO/LASCO-C3. Thompson and Reginald (2008) determined the photometric conversion from DN s−1 to mean solar brightness for STEREO/COR-1 using observations of Jupiter. Buffington et al.(2007) compare the photometric response of the Coriolis/SMEI and SOHO/LASCO-C3 using 17 stars that are observed by both instruments.”

So far so good.

“For HI-1, a given star takes typically ∼20 days to traverse the FOV. One mean solar brightness (Bsun) unit is the average surface brightness of the solar disk, if an instrument were to observe the Sun directly. One S10 unit is defined as the diffuse flux corresponding to one 10th visual magnitude star per square degree of sky”.

Damn, no mention of zodiacal light. No mention of scattering of sunlight.

All they’re testing is instrument optics.

They are measuring light curves for variable stars in HI-1 but, in the example given they’ve chosen a really bright eclipsing binary, magnitude 7 to 7.5, nowhere near as faint as i’m hoping for.

OK, let’s move over to this paper. “Considerations for the Use of STEREO-HI Data for Astronomical Studies”. See if it has anything on zodiacal light.

https://iopscience.iop.org/article/10.3847/1538-3881/aa6349/pdf

No mention of zodiacal light.

“HI-1. The reason is that at the sunward edge of the field of view, the F-coronal background is about 60% of the saturation level (Eyles et al.2009), while at the anti-sunward edge it is only about 1%. In HI-2 the maximum F-coronal signal is only about 10% of the saturation level”

Now that’s important. It’s the first mention of the relative strength of near-sun scattered light that i’ve found. How does that compare with star brightness?

See following image. Drop in star brightness after removing background light from the corona. HI-2 at top and HI-1 below. This is bad, very bad. Significant drop in brightness even for very bright stars, (almost naked eye visible). Not sure if this is a correctable error, it may be.

Saturation only starts to occur for stars brighter than magnitude 3.5 (HI-2) and magnitude 5 (HI-1). So, comparing with the above, magnitude 5 is about 100% – 60% = 40% of saturation. Magnitude 3.5 is about 100%-10% = 90% of saturation.

> https://iopscience.iop.org/article/10.3847/1538-3881/aa6349/pdf

> “HI-1. The reason is that at the sunward edge of the field of view, the F-coronal background is about 60% of the saturation level (Eyles et al.2009), while at the anti-sunward edge it is only about 1%. In HI-2 the maximum F-coronal signal is only about 10% of the saturation level”.

So, following up on that lead – actually two leads isn’t it: “Eyles (2009)” and “F-coronal”

Eyles paper is “The Heliospheric Imagers Onboard the STEREO Mission”. 59 pages.
https://sci-hub.tw/10.1007/s11207-008-9299-0

I’m going around in circles. I quoted from that paper earlier in this thread. Looking further down. in the paper.

“the zodiacal light or F-corona, according to the model of Koutchmy and Lamy (1985)”

Yeah figured. Ancient damn references again.

Paper Koutchmy and Lamy (1985) is not found on Google Scholar. Correction, it is there, but in a different journal with a different title.

https://sci-hub.tw/10.1017/s0252921100084359

“Originally the Fraunhofer corona, the F-corona together with the K-corona forms the solar corona conspicuously seen during total solar eclipses. The dominating K-corona (more than 90 % of the coronal brightness) is produced by solar light scattered by free electrons; it is characterized by the absence of Fraunhofer lines of the solar spectrum which are completely smeared out by the large Doppler shifts of the high velocity electrons of the corona. The F-corona is the component of the corona light which does exhibit solar Fraunhofer lines which enabled to recognize it as the inner Zodiacal Light caused by light scattering off interplanetary dust grains.”

“Recent progress”

Yeah, recent, spanning 1953 to 1982.

“Once the luminance of K+F has been obtained as a function of solar distance after proper corrections for sky and instrumental backgrounds … “

Ah, here we go, this is what i’m looking for, the 2-D distribution of zodiacal light from 5 to 60 degrees from the Sun. Only one slight catch – it’s wrong. Or, being kind, grossly incomplete. The actual light distribution is nowhere near ellipsoidal, so using the equatorial and polar data together doesn’t suffice.

mollwollfumble said:

> https://iopscience.iop.org/article/10.3847/1538-3881/aa6349/pdf

> “HI-1. The reason is that at the sunward edge of the field of view, the F-coronal background is about 60% of the saturation level (Eyles et al.2009), while at the anti-sunward edge it is only about 1%. In HI-2 the maximum F-coronal signal is only about 10% of the saturation level”.

So, following up on that lead – actually two leads isn’t it: “Eyles (2009)” and “F-coronal”

Eyles paper is “The Heliospheric Imagers Onboard the STEREO Mission”. 59 pages.
https://sci-hub.tw/10.1007/s11207-008-9299-0

I’m going around in circles. I quoted from that paper earlier in this thread. Looking further down. in the paper.

“the zodiacal light or F-corona, according to the model of Koutchmy and Lamy (1985)”

Yeah figured. Ancient damn references again.

Paper Koutchmy and Lamy (1985) is not found on Google Scholar. Correction, it is there, but in a different journal with a different title.

https://sci-hub.tw/10.1017/s0252921100084359

“Originally the Fraunhofer corona, the F-corona together with the K-corona forms the solar corona conspicuously seen during total solar eclipses. The dominating K-corona (more than 90 % of the coronal brightness) is produced by solar light scattered by free electrons; it is characterized by the absence of Fraunhofer lines of the solar spectrum which are completely smeared out by the large Doppler shifts of the high velocity electrons of the corona. The F-corona is the component of the corona light which does exhibit solar Fraunhofer lines which enabled to recognize it as the inner Zodiacal Light caused by light scattering off interplanetary dust grains.”

“Recent progress”

Yeah, recent, spanning 1953 to 1982.

“Once the luminance of K+F has been obtained as a function of solar distance after proper corrections for sky and instrumental backgrounds … “

Ah, here we go, this is what i’m looking for, the 2-D distribution of zodiacal light from 5 to 60 degrees from the Sun. Only one slight catch – it’s wrong. Or, being kind, grossly incomplete. The actual light distribution is nowhere near ellipsoidal, so using the equatorial and polar data together doesn’t suffice.

OK, so it’s “grossly incomplete”, but at this stage it is good enough for me. Is there a better?

Here’s a more recent paper from 2018 that may have something. “Characterization of the White-Light F-Corona from STEREO/SECCHI Observations”.

https://meetingorganizer.copernicus.org/EGU2018/EGU2018-18395-1.pdf

Oh drat, it’s just an abstract.

“The values derived are slightly different from the parameters determined from the Helios mission. The inferred center of symmetry is not at the Sun’s center, but is offset by about 0.5 solar radii in the direction of the average position of Jupiter. The brightness of the F-corona is very dependent on the exact location of STEREO-A along its orbit “

Trying again. This is better. “Characterization of the White-light Brightness of the F-corona between 5° and 24° Elongation”

https://iopscience.iop.org/article/10.3847/1538-4357/aacea3/meta

“We found that the brightness profiles can be approximated by power laws, with the coefficients of the models depending upon the observer’s ecliptic longitude.”

Old values from Helios. “From 11 years of observations of the ZL obtained using the Zodiacal Light Photometers (ZLP; Leinert et al. 1975) on board the two Helios spacecraft (Porsche 1981), Leinert et al. (1982) found that the intensity of the ZL was very stable with less than a 2% variation. Leinert et al. (1981) found that the radial intensity of the ZL between 0.3 and 1.0 au decreases with heliocentric distance R as R^-2.30 +- 0.05, where the upper and lower limits of the exponent correspond to the smallest and the largest elongations from the Sun, respectively.”

Now, just add some numbers to these contours, please.

That’s better. Not numbers, but at least real contours.

And numbers above. Good.

“A quick look at the isocontours in Figure 2 clearly shows that the F-corona shape resembles, to first approximation, that of a superellipse with 1 < n < 2”.

Superellipse. I didn’t expect that, but it fits the data. n=2 is an ellipse. From the following graph, n ~ 1.6.

mollwollfumble said:

mollwollfumble said:

> https://iopscience.iop.org/article/10.3847/1538-3881/aa6349/pdf

> “HI-1. The reason is that at the sunward edge of the field of view, the F-coronal background is about 60% of the saturation level (Eyles et al.2009), while at the anti-sunward edge it is only about 1%. In HI-2 the maximum F-coronal signal is only about 10% of the saturation level”.

So, following up on that lead – actually two leads isn’t it: “Eyles (2009)” and “F-coronal”

Eyles paper is “The Heliospheric Imagers Onboard the STEREO Mission”. 59 pages.
https://sci-hub.tw/10.1007/s11207-008-9299-0

I’m going around in circles. I quoted from that paper earlier in this thread. Looking further down. in the paper.

“the zodiacal light or F-corona, according to the model of Koutchmy and Lamy (1985)”

Yeah figured. Ancient damn references again.

Paper Koutchmy and Lamy (1985) is not found on Google Scholar. Correction, it is there, but in a different journal with a different title.

https://sci-hub.tw/10.1017/s0252921100084359

“Originally the Fraunhofer corona, the F-corona together with the K-corona forms the solar corona conspicuously seen during total solar eclipses. The dominating K-corona (more than 90 % of the coronal brightness) is produced by solar light scattered by free electrons; it is characterized by the absence of Fraunhofer lines of the solar spectrum which are completely smeared out by the large Doppler shifts of the high velocity electrons of the corona. The F-corona is the component of the corona light which does exhibit solar Fraunhofer lines which enabled to recognize it as the inner Zodiacal Light caused by light scattering off interplanetary dust grains.”

“Recent progress”

Yeah, recent, spanning 1953 to 1982.

“Once the luminance of K+F has been obtained as a function of solar distance after proper corrections for sky and instrumental backgrounds … “

Ah, here we go, this is what i’m looking for, the 2-D distribution of zodiacal light from 5 to 60 degrees from the Sun. Only one slight catch – it’s wrong. Or, being kind, grossly incomplete. The actual light distribution is nowhere near ellipsoidal, so using the equatorial and polar data together doesn’t suffice.

OK, so it’s “grossly incomplete”, but at this stage it is good enough for me. Is there a better?

Here’s a more recent paper from 2018 that may have something. “Characterization of the White-Light F-Corona from STEREO/SECCHI Observations”.

https://meetingorganizer.copernicus.org/EGU2018/EGU2018-18395-1.pdf

Oh drat, it’s just an abstract.

“The values derived are slightly different from the parameters determined from the Helios mission. The inferred center of symmetry is not at the Sun’s center, but is offset by about 0.5 solar radii in the direction of the average position of Jupiter. The brightness of the F-corona is very dependent on the exact location of STEREO-A along its orbit “

Trying again. This is better. “Characterization of the White-light Brightness of the F-corona between 5° and 24° Elongation”

https://iopscience.iop.org/article/10.3847/1538-4357/aacea3/meta

“We found that the brightness profiles can be approximated by power laws, with the coefficients of the models depending upon the observer’s ecliptic longitude.”

Old values from Helios. “From 11 years of observations of the ZL obtained using the Zodiacal Light Photometers (ZLP; Leinert et al. 1975) on board the two Helios spacecraft (Porsche 1981), Leinert et al. (1982) found that the intensity of the ZL was very stable with less than a 2% variation. Leinert et al. (1981) found that the radial intensity of the ZL between 0.3 and 1.0 au decreases with heliocentric distance R as R^-2.30 +- 0.05, where the upper and lower limits of the exponent correspond to the smallest and the largest elongations from the Sun, respectively.”

Now, just add some numbers to these contours, please.

That’s better. Not numbers, but at least real contours.

And numbers above. Good.

“A quick look at the isocontours in Figure 2 clearly shows that the F-corona shape resembles, to first approximation, that of a superellipse with 1 < n < 2”.

Superellipse. I didn’t expect that, but it fits the data. n=2 is an ellipse. From the following graph, n ~ 1.6.

So far so good. But what to do with that information?

We have an astronomical object, be it a near Earth asteroid or distant galaxy, we have a background light source in the zodiacal light. How do we find the magnitude of astronomical object that will be invisible against the background?

A memory twiggs me. Shot noise. (I keep miscalling is Schott noise because it was discovered by Schottky)

But before that, surface brightness and point spread function. A galaxy has wide physical extent and therefore low surface brightness, which makes it much more difficult to see against a uniform irregular background than a star.

Point spread function (psf) is the smearing of a point of light, a star, by the optics, this can and usually does exceed the size of a pixel. The more the starlight is smeared, the more difficult it is to see against the background. But conversely, the narrower the point spread function the less accurate the measure of brightness is going to be. In addition, narrow psfs also cause saturation problems. Telescopes such as WISE use dithering to increase the size of the psf – very effectively – to give really accurate measurements of brightness and colour. But that would result in an enormous reduction in signal to noise ratio.

Now Shot noise. Shot noise occurs in photon counting in optical devices, where shot noise is associated with the particle nature of light. It is modelled as a poisson process. It appears as a graininess in low light photographs.

The signal to noise ratio (standard deviation) is the square root of the number of photons counted.

So let’s see if I can apply this. Suppose zodiacal light has a count of 10,000 photons at a given pixel. Then the noise generated by that is sqrt(10,000) = 100 photons. Then if a star has a count of 100 photons at that pixel then the star is completely indistinguishable from random noise.

The zodiacal light 15 degrees from the Sun is 100 times as high as at the best viewing angle, so we lose a factor of 10 in visible brightness, which is magnitude … “a difference of 1.0 in magnitude corresponds to a brightness ratio of ⁵√100 = 2.512. So a factor of 10 in brightness is a loss in visible magnitude of 2.5.

Not too bad. But that’s only to 15 degrees from the Sun. Between 15 and 5 degrees from the Sun we lose … um … the zodiacal light is 10 times as bright, another loss in visual magnitude of 1.25.

Hmm. Again not too bad, unless I’ve miscalculated.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

> https://iopscience.iop.org/article/10.3847/1538-3881/aa6349/pdf

> “HI-1. The reason is that at the sunward edge of the field of view, the F-coronal background is about 60% of the saturation level (Eyles et al.2009), while at the anti-sunward edge it is only about 1%. In HI-2 the maximum F-coronal signal is only about 10% of the saturation level”.

So, following up on that lead – actually two leads isn’t it: “Eyles (2009)” and “F-coronal”

Eyles paper is “The Heliospheric Imagers Onboard the STEREO Mission”. 59 pages.
https://sci-hub.tw/10.1007/s11207-008-9299-0

I’m going around in circles. I quoted from that paper earlier in this thread. Looking further down. in the paper.

“the zodiacal light or F-corona, according to the model of Koutchmy and Lamy (1985)”

Yeah figured. Ancient damn references again.

Paper Koutchmy and Lamy (1985) is not found on Google Scholar. Correction, it is there, but in a different journal with a different title.

https://sci-hub.tw/10.1017/s0252921100084359

“Originally the Fraunhofer corona, the F-corona together with the K-corona forms the solar corona conspicuously seen during total solar eclipses. The dominating K-corona (more than 90 % of the coronal brightness) is produced by solar light scattered by free electrons; it is characterized by the absence of Fraunhofer lines of the solar spectrum which are completely smeared out by the large Doppler shifts of the high velocity electrons of the corona. The F-corona is the component of the corona light which does exhibit solar Fraunhofer lines which enabled to recognize it as the inner Zodiacal Light caused by light scattering off interplanetary dust grains.”

“Recent progress”

Yeah, recent, spanning 1953 to 1982.

“Once the luminance of K+F has been obtained as a function of solar distance after proper corrections for sky and instrumental backgrounds … “

Ah, here we go, this is what i’m looking for, the 2-D distribution of zodiacal light from 5 to 60 degrees from the Sun. Only one slight catch – it’s wrong. Or, being kind, grossly incomplete. The actual light distribution is nowhere near ellipsoidal, so using the equatorial and polar data together doesn’t suffice.

OK, so it’s “grossly incomplete”, but at this stage it is good enough for me. Is there a better?

Here’s a more recent paper from 2018 that may have something. “Characterization of the White-Light F-Corona from STEREO/SECCHI Observations”.

https://meetingorganizer.copernicus.org/EGU2018/EGU2018-18395-1.pdf

Oh drat, it’s just an abstract.

“The values derived are slightly different from the parameters determined from the Helios mission. The inferred center of symmetry is not at the Sun’s center, but is offset by about 0.5 solar radii in the direction of the average position of Jupiter. The brightness of the F-corona is very dependent on the exact location of STEREO-A along its orbit “

Trying again. This is better. “Characterization of the White-light Brightness of the F-corona between 5° and 24° Elongation”

https://iopscience.iop.org/article/10.3847/1538-4357/aacea3/meta

“We found that the brightness profiles can be approximated by power laws, with the coefficients of the models depending upon the observer’s ecliptic longitude.”

Old values from Helios. “From 11 years of observations of the ZL obtained using the Zodiacal Light Photometers (ZLP; Leinert et al. 1975) on board the two Helios spacecraft (Porsche 1981), Leinert et al. (1982) found that the intensity of the ZL was very stable with less than a 2% variation. Leinert et al. (1981) found that the radial intensity of the ZL between 0.3 and 1.0 au decreases with heliocentric distance R as R^-2.30 +- 0.05, where the upper and lower limits of the exponent correspond to the smallest and the largest elongations from the Sun, respectively.”

Now, just add some numbers to these contours, please.

That’s better. Not numbers, but at least real contours.

And numbers above. Good.

“A quick look at the isocontours in Figure 2 clearly shows that the F-corona shape resembles, to first approximation, that of a superellipse with 1 < n < 2”.

Superellipse. I didn’t expect that, but it fits the data. n=2 is an ellipse. From the following graph, n ~ 1.6.

So far so good. But what to do with that information?

We have an astronomical object, be it a near Earth asteroid or distant galaxy, we have a background light source in the zodiacal light. How do we find the magnitude of astronomical object that will be invisible against the background?

A memory twiggs me. Shot noise. (I keep miscalling is Schott noise because it was discovered by Schottky)

But before that, surface brightness and point spread function. A galaxy has wide physical extent and therefore low surface brightness, which makes it much more difficult to see against a uniform irregular background than a star.

Point spread function (psf) is the smearing of a point of light, a star, by the optics, this can and usually does exceed the size of a pixel. The more the starlight is smeared, the more difficult it is to see against the background. But conversely, the narrower the point spread function the less accurate the measure of brightness is going to be. In addition, narrow psfs also cause saturation problems. Telescopes such as WISE use dithering to increase the size of the psf – very effectively – to give really accurate measurements of brightness and colour. But that would result in an enormous reduction in signal to noise ratio.

Now Shot noise. Shot noise occurs in photon counting in optical devices, where shot noise is associated with the particle nature of light. It is modelled as a poisson process. It appears as a graininess in low light photographs.

The signal to noise ratio (standard deviation) is the square root of the number of photons counted.

So let’s see if I can apply this. Suppose zodiacal light has a count of 10,000 photons at a given pixel. Then the noise generated by that is sqrt(10,000) = 100 photons. Then if a star has a count of 100 photons at that pixel then the star is completely indistinguishable from random noise.

The zodiacal light 15 degrees from the Sun is 100 times as high as at the best viewing angle, so we lose a factor of 10 in visible brightness, which is magnitude … “a difference of 1.0 in magnitude corresponds to a brightness ratio of ⁵√100 = 2.512. So a factor of 10 in brightness is a loss in visible magnitude of 2.5.

Not too bad. But that’s only to 15 degrees from the Sun. Between 15 and 5 degrees from the Sun we lose … um … the zodiacal light is 10 times as bright, another loss in visual magnitude of 1.25.

Hmm. Again not too bad, unless I’ve miscalculated.

I have miscalculated.

Oh stuff it. Time for a complete redesign

Neutrino was right. The inner zodiacal light is just too difficult to see though. The only way around it is to move the Sun physically out of the way, and that eliminates the following orbits:

• All Earth orbits, the Moon’s surface, all lunar orbits, Sun-Earth lagrangian points 1 and 2.

The cheapest remaining orbits are Earth-leading and Earth-trailing orbits used by spacecraft Spitzer and STEREO. Then perhaps stopping it at or near lagrangian points L4 / L5.

That means a redesign for a whole host of reasons:

• much longer viewing times needed for cosmic ray rejection.
• very much slower communications.
• the whole concept of spacecraft spin needs a complete rethink – it’s great for wide field of view but bad for telescope stability. It no longer helps solar panel pointing. And leaves a big chunk of Sun within the field of view.
• need to view between Earth and Sun as well as away from Sun means multiple telescopes.
• How to get that enormous field of view without mosaicing or spinning, or losing resolution – seems impossible.

The only new idea i’ve come up with is a mirror on gimbals. The telescope points in a constant direction but the lightweight perfect mirror moves, allowing multiple pointing directions. ¿But can such a mirror be lightweight and perfect enough, temperature changes would make it warp for a start, and there’s the problem of stopping and starting the movement.

“Life is struggle”, Buddah.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

OK, so it’s “grossly incomplete”, but at this stage it is good enough for me. Is there a better?

Here’s a more recent paper from 2018 that may have something. “Characterization of the White-Light F-Corona from STEREO/SECCHI Observations”.

https://meetingorganizer.copernicus.org/EGU2018/EGU2018-18395-1.pdf

Oh drat, it’s just an abstract.

“The values derived are slightly different from the parameters determined from the Helios mission. The inferred center of symmetry is not at the Sun’s center, but is offset by about 0.5 solar radii in the direction of the average position of Jupiter. The brightness of the F-corona is very dependent on the exact location of STEREO-A along its orbit “

Trying again. This is better. “Characterization of the White-light Brightness of the F-corona between 5° and 24° Elongation”

https://iopscience.iop.org/article/10.3847/1538-4357/aacea3/meta

“We found that the brightness profiles can be approximated by power laws, with the coefficients of the models depending upon the observer’s ecliptic longitude.”

Old values from Helios. “From 11 years of observations of the ZL obtained using the Zodiacal Light Photometers (ZLP; Leinert et al. 1975) on board the two Helios spacecraft (Porsche 1981), Leinert et al. (1982) found that the intensity of the ZL was very stable with less than a 2% variation. Leinert et al. (1981) found that the radial intensity of the ZL between 0.3 and 1.0 au decreases with heliocentric distance R as R^-2.30 +- 0.05, where the upper and lower limits of the exponent correspond to the smallest and the largest elongations from the Sun, respectively.”

Now, just add some numbers to these contours, please.

That’s better. Not numbers, but at least real contours.

And numbers above. Good.

“A quick look at the isocontours in Figure 2 clearly shows that the F-corona shape resembles, to first approximation, that of a superellipse with 1 < n < 2”.

Superellipse. I didn’t expect that, but it fits the data. n=2 is an ellipse. From the following graph, n ~ 1.6.

So far so good. But what to do with that information?

We have an astronomical object, be it a near Earth asteroid or distant galaxy, we have a background light source in the zodiacal light. How do we find the magnitude of astronomical object that will be invisible against the background?

A memory twiggs me. Shot noise. (I keep miscalling is Schott noise because it was discovered by Schottky)

But before that, surface brightness and point spread function. A galaxy has wide physical extent and therefore low surface brightness, which makes it much more difficult to see against a uniform irregular background than a star.

Point spread function (psf) is the smearing of a point of light, a star, by the optics, this can and usually does exceed the size of a pixel. The more the starlight is smeared, the more difficult it is to see against the background. But conversely, the narrower the point spread function the less accurate the measure of brightness is going to be. In addition, narrow psfs also cause saturation problems. Telescopes such as WISE use dithering to increase the size of the psf – very effectively – to give really accurate measurements of brightness and colour. But that would result in an enormous reduction in signal to noise ratio.

Now Shot noise. Shot noise occurs in photon counting in optical devices, where shot noise is associated with the particle nature of light. It is modelled as a poisson process. It appears as a graininess in low light photographs.

The signal to noise ratio (standard deviation) is the square root of the number of photons counted.

So let’s see if I can apply this. Suppose zodiacal light has a count of 10,000 photons at a given pixel. Then the noise generated by that is sqrt(10,000) = 100 photons. Then if a star has a count of 100 photons at that pixel then the star is completely indistinguishable from random noise.

The zodiacal light 15 degrees from the Sun is 100 times as high as at the best viewing angle, so we lose a factor of 10 in visible brightness, which is magnitude … “a difference of 1.0 in magnitude corresponds to a brightness ratio of ⁵√100 = 2.512. So a factor of 10 in brightness is a loss in visible magnitude of 2.5.

Not too bad. But that’s only to 15 degrees from the Sun. Between 15 and 5 degrees from the Sun we lose … um … the zodiacal light is 10 times as bright, another loss in visual magnitude of 1.25.

Hmm. Again not too bad, unless I’ve miscalculated.

I have miscalculated.

Oh stuff it. Time for a complete redesign

Neutrino was right. The inner zodiacal light is just too difficult to see though. The only way around it is to move the Sun physically out of the way, and that eliminates the following orbits:

• All Earth orbits, the Moon’s surface, all lunar orbits, Sun-Earth lagrangian points 1 and 2.

The cheapest remaining orbits are Earth-leading and Earth-trailing orbits used by spacecraft Spitzer and STEREO. Then perhaps stopping it at or near lagrangian points L4 / L5.

That means a redesign for a whole host of reasons:

• much longer viewing times needed for cosmic ray rejection.
• very much slower communications.
• the whole concept of spacecraft spin needs a complete rethink – it’s great for wide field of view but bad for telescope stability. It no longer helps solar panel pointing. And leaves a big chunk of Sun within the field of view.
• need to view between Earth and Sun as well as away from Sun means multiple telescopes.
• How to get that enormous field of view without mosaicing or spinning, or losing resolution – seems impossible.

The only new idea i’ve come up with is a mirror on gimbals. The telescope points in a constant direction but the lightweight perfect mirror moves, allowing multiple pointing directions. ¿But can such a mirror be lightweight and perfect enough, temperature changes would make it warp for a start, and there’s the problem of stopping and starting the movement.

“Life is struggle”, Buddah.

I’ve now expanded that to two options.

1. Abandon the inner two rows of the original design making the annulus 15 to 60 degrees rather than 5 to 60 degrees. But otherwise keep the design the same. Advantage, protected from cosmic rays and faster comunications time.

2. Earth leading (or trailing) orbit around the Sun with a rectangular field of view perhaps 60 degrees by 60 degrees in all using a fixed-axis rotating mirror (not gimbals) to scan the field of view with a quasi-1D sensor array. Advantage, avoid the zodiacal light. Perhaps the whole telescope could rotate, like Gaia.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

So far so good. But what to do with that information?

We have an astronomical object, be it a near Earth asteroid or distant galaxy, we have a background light source in the zodiacal light. How do we find the magnitude of astronomical object that will be invisible against the background?

A memory twiggs me. Shot noise. (I keep miscalling is Schott noise because it was discovered by Schottky)

But before that, surface brightness and point spread function. A galaxy has wide physical extent and therefore low surface brightness, which makes it much more difficult to see against a uniform irregular background than a star.

Point spread function (psf) is the smearing of a point of light, a star, by the optics, this can and usually does exceed the size of a pixel. The more the starlight is smeared, the more difficult it is to see against the background. But conversely, the narrower the point spread function the less accurate the measure of brightness is going to be. In addition, narrow psfs also cause saturation problems. Telescopes such as WISE use dithering to increase the size of the psf – very effectively – to give really accurate measurements of brightness and colour. But that would result in an enormous reduction in signal to noise ratio.

Now Shot noise. Shot noise occurs in photon counting in optical devices, where shot noise is associated with the particle nature of light. It is modelled as a poisson process. It appears as a graininess in low light photographs.

The signal to noise ratio (standard deviation) is the square root of the number of photons counted.

So let’s see if I can apply this. Suppose zodiacal light has a count of 10,000 photons at a given pixel. Then the noise generated by that is sqrt(10,000) = 100 photons. Then if a star has a count of 100 photons at that pixel then the star is completely indistinguishable from random noise.

The zodiacal light 15 degrees from the Sun is 100 times as high as at the best viewing angle, so we lose a factor of 10 in visible brightness, which is magnitude … “a difference of 1.0 in magnitude corresponds to a brightness ratio of ⁵√100 = 2.512. So a factor of 10 in brightness is a loss in visible magnitude of 2.5.

Not too bad. But that’s only to 15 degrees from the Sun. Between 15 and 5 degrees from the Sun we lose … um … the zodiacal light is 10 times as bright, another loss in visual magnitude of 1.25.

Hmm. Again not too bad, unless I’ve miscalculated.

I have miscalculated.

Oh stuff it. Time for a complete redesign

Neutrino was right. The inner zodiacal light is just too difficult to see though. The only way around it is to move the Sun physically out of the way, and that eliminates the following orbits:

• All Earth orbits, the Moon’s surface, all lunar orbits, Sun-Earth lagrangian points 1 and 2.

The cheapest remaining orbits are Earth-leading and Earth-trailing orbits used by spacecraft Spitzer and STEREO. Then perhaps stopping it at or near lagrangian points L4 / L5.

That means a redesign for a whole host of reasons:

• much longer viewing times needed for cosmic ray rejection.
• very much slower communications.
• the whole concept of spacecraft spin needs a complete rethink – it’s great for wide field of view but bad for telescope stability. It no longer helps solar panel pointing. And leaves a big chunk of Sun within the field of view.
• need to view between Earth and Sun as well as away from Sun means multiple telescopes.
• How to get that enormous field of view without mosaicing or spinning, or losing resolution – seems impossible.

The only new idea i’ve come up with is a mirror on gimbals. The telescope points in a constant direction but the lightweight perfect mirror moves, allowing multiple pointing directions. ¿But can such a mirror be lightweight and perfect enough, temperature changes would make it warp for a start, and there’s the problem of stopping and starting the movement.

“Life is struggle”, Buddah.

I’ve now expanded that to two options.

1. Abandon the inner two rows of the original design making the annulus 15 to 60 degrees rather than 5 to 60 degrees. But otherwise keep the design the same. Advantage, protected from cosmic rays and faster communications time.

2. Earth leading (or trailing) orbit around the Sun with a rectangular field of view perhaps 60 degrees by 60 degrees in all using a fixed-axis rotating mirror (not gimbals) to scan the field of view with a quasi-1D sensor array. Advantage, avoid the zodiacal light. Perhaps the whole telescope could rotate, like Gaia.

What if – there’s a third option.

3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides. If possible, this would have the advantage of looking over the poles of the Sun most of the time where the zodiacal light is faintest, rather than in the ecliptic plane where the zodiacal light is brightest. That would tend to mean a closer orbit and faster communications than an Earth leading (or trailing) orbit.

But how big is the largest such orbit? And how far is it off circular?

In the line directly between Earth and Sun, such an orbit has to be constrained between L1 and L2, which are pretty close to Earth, but way further out than the moon. Along the line of the Earth’s motion, the orbit has be be constrained between L4 and L5 which are a long way apart. But what of the polar direction, ie. orbital inclination > 5 degrees around the Sun?

By that I mean orbits not too different to those of Helios A and Helios B, but designed to have the same orbital period around the Sun as the Earth, The Helios spacecraft have a shorter orbit. But like Helios the orbit would be (close to) elliptical around the Sun rather than circular.

“Quasi-satellites are co-orbital objects that librate around 0° from the primary. Low-eccentricity quasi-satellite orbits are highly unstable, but for moderate to high eccentricities such orbits can be stable. From a co-rotating perspective the quasi-satellite appears to orbit the primary like a retrograde satellite.”

That’s what I’m talking about, unless they’re ignoring the inclination. Checking reference: “we assume that both planets share the same orbital plane” ie. inclination zero. Darn it that’s useless, I’d already figured out the approximate maths for that 30 years ago.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

I have miscalculated.

Oh stuff it. Time for a complete redesign

Neutrino was right. The inner zodiacal light is just too difficult to see though. The only way around it is to move the Sun physically out of the way, and that eliminates the following orbits:

• All Earth orbits, the Moon’s surface, all lunar orbits, Sun-Earth lagrangian points 1 and 2.

The cheapest remaining orbits are Earth-leading and Earth-trailing orbits used by spacecraft Spitzer and STEREO. Then perhaps stopping it at or near lagrangian points L4 / L5.

That means a redesign for a whole host of reasons:

• much longer viewing times needed for cosmic ray rejection.
• very much slower communications.
• the whole concept of spacecraft spin needs a complete rethink – it’s great for wide field of view but bad for telescope stability. It no longer helps solar panel pointing. And leaves a big chunk of Sun within the field of view.
• need to view between Earth and Sun as well as away from Sun means multiple telescopes.
• How to get that enormous field of view without mosaicing or spinning, or losing resolution – seems impossible.

The only new idea i’ve come up with is a mirror on gimbals. The telescope points in a constant direction but the lightweight perfect mirror moves, allowing multiple pointing directions. ¿But can such a mirror be lightweight and perfect enough, temperature changes would make it warp for a start, and there’s the problem of stopping and starting the movement.

“Life is struggle”, Buddah.

I’ve now expanded that to two options.

1. Abandon the inner two rows of the original design making the annulus 15 to 60 degrees rather than 5 to 60 degrees. But otherwise keep the design the same. Advantage, protected from cosmic rays and faster communications time.

2. Earth leading (or trailing) orbit around the Sun with a rectangular field of view perhaps 60 degrees by 60 degrees in all using a fixed-axis rotating mirror (not gimbals) to scan the field of view with a quasi-1D sensor array. Advantage, avoid the zodiacal light. Perhaps the whole telescope could rotate, like Gaia.

What if – there’s a third option.

3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides. If possible, this would have the advantage of looking over the poles of the Sun most of the time where the zodiacal light is faintest, rather than in the ecliptic plane where the zodiacal light is brightest. That would tend to mean a closer orbit and faster communications than an Earth leading (or trailing) orbit.

But how big is the largest such orbit? And how far is it off circular?

In the line directly between Earth and Sun, such an orbit has to be constrained between L1 and L2, which are pretty close to Earth, but way further out than the moon. Along the line of the Earth’s motion, the orbit has be be constrained between L4 and L5 which are a long way apart. But what of the polar direction, ie. orbital inclination > 5 degrees around the Sun?

By that I mean orbits not too different to those of Helios A and Helios B, but designed to have the same orbital period around the Sun as the Earth, The Helios spacecraft have a shorter orbit. But like Helios the orbit would be (close to) elliptical around the Sun rather than circular.

“Quasi-satellites are co-orbital objects that librate around 0° from the primary. Low-eccentricity quasi-satellite orbits are highly unstable, but for moderate to high eccentricities such orbits can be stable. From a co-rotating perspective the quasi-satellite appears to orbit the primary like a retrograde satellite.”

That’s what I’m talking about, unless they’re ignoring the inclination. Checking reference: “we assume that both planets share the same orbital plane” ie. inclination zero. Darn it that’s useless, I’d already figured out the approximate maths for that 30 years ago.

> 3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides.

It has to work.

For every inclination there is an eccentricity that gives a quasi-circular 1:1 resonant orbit about the Earth when viewed along the Earth-Sun axis. It’s easier to calculate the other way around – given an eccentricity calculate an inclination. For mild inclinations the eccentricity increases with inclination. For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations. I’m not al all interested in orbital inclinations exceeding 45 degrees.

The simplest calculation method requires Kepler’s third law, equal arc areas in equal times. The simplest approximation replaces the ellipse with an offset circle (Copernicus’s approximation), which works for small eccentricities. But I might be able to go full ellipse in Excel.

I’ve been making calculation errors lately, let’s hope I don’t stuff this one up.

For even better vision, make the orbit quasi-elliptical (around the centre not the focal point) when viewed along the Earth-Sun axis to give the same zodiacal light seeing conditions in the ecliptic plane and off the ecliptic plane. The calculation is not – in principle – more difficult.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

I’ve now expanded that to two options.

1. Abandon the inner two rows of the original design making the annulus 15 to 60 degrees rather than 5 to 60 degrees. But otherwise keep the design the same. Advantage, protected from cosmic rays and faster communications time.

2. Earth leading (or trailing) orbit around the Sun with a rectangular field of view perhaps 60 degrees by 60 degrees in all using a fixed-axis rotating mirror (not gimbals) to scan the field of view with a quasi-1D sensor array. Advantage, avoid the zodiacal light. Perhaps the whole telescope could rotate, like Gaia.

What if – there’s a third option.

3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides. If possible, this would have the advantage of looking over the poles of the Sun most of the time where the zodiacal light is faintest, rather than in the ecliptic plane where the zodiacal light is brightest. That would tend to mean a closer orbit and faster communications than an Earth leading (or trailing) orbit.

But how big is the largest such orbit? And how far is it off circular?

In the line directly between Earth and Sun, such an orbit has to be constrained between L1 and L2, which are pretty close to Earth, but way further out than the moon. Along the line of the Earth’s motion, the orbit has be be constrained between L4 and L5 which are a long way apart. But what of the polar direction, ie. orbital inclination > 5 degrees around the Sun?

By that I mean orbits not too different to those of Helios A and Helios B, but designed to have the same orbital period around the Sun as the Earth, The Helios spacecraft have a shorter orbit. But like Helios the orbit would be (close to) elliptical around the Sun rather than circular.

“Quasi-satellites are co-orbital objects that librate around 0° from the primary. Low-eccentricity quasi-satellite orbits are highly unstable, but for moderate to high eccentricities such orbits can be stable. From a co-rotating perspective the quasi-satellite appears to orbit the primary like a retrograde satellite.”

That’s what I’m talking about, unless they’re ignoring the inclination. Checking reference: “we assume that both planets share the same orbital plane” ie. inclination zero. Darn it that’s useless, I’d already figured out the approximate maths for that 30 years ago.

> 3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides.

It has to work.

For every inclination there is an eccentricity that gives a quasi-circular 1:1 resonant orbit about the Earth when viewed along the Earth-Sun axis. It’s easier to calculate the other way around – given an eccentricity calculate an inclination. For mild inclinations the eccentricity increases with inclination. For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations. I’m not al all interested in orbital inclinations exceeding 45 degrees.

The simplest calculation method requires Kepler’s third law, equal arc areas in equal times. The simplest approximation replaces the ellipse with an offset circle (Copernicus’s approximation), which works for small eccentricities. But I might be able to go full ellipse in Excel.

I’ve been making calculation errors lately, let’s hope I don’t stuff this one up.

For even better vision, make the orbit quasi-elliptical (around the centre not the focal point) when viewed along the Earth-Sun axis to give the same zodiacal light seeing conditions in the ecliptic plane and off the ecliptic plane. The calculation is not – in principle – more difficult.

I know what you’re asking yourself. The Earth’s orbit isn’t perfectly circular. Does this make things harder or easier. Easier, in the sense that it allows the spacecraft orbit to be more circular, although it fixes the axis of the inclination to be parallel to the minor axis of the Earth’s ellipse. For easy of calculation, ignore the Earth’s eccentricity of orbit.

> For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations.

Um, no. For 90 degree inclination the orbit viewed along the Earth-Sun axis is close to a semicircle, not a full circle. The semicircle is traversed backwards an forwards once each year. Ignore that strategy for small inclinations.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

What if – there’s a third option.

3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides. If possible, this would have the advantage of looking over the poles of the Sun most of the time where the zodiacal light is faintest, rather than in the ecliptic plane where the zodiacal light is brightest. That would tend to mean a closer orbit and faster communications than an Earth leading (or trailing) orbit.

But how big is the largest such orbit? And how far is it off circular?

In the line directly between Earth and Sun, such an orbit has to be constrained between L1 and L2, which are pretty close to Earth, but way further out than the moon. Along the line of the Earth’s motion, the orbit has be be constrained between L4 and L5 which are a long way apart. But what of the polar direction, ie. orbital inclination > 5 degrees around the Sun?

By that I mean orbits not too different to those of Helios A and Helios B, but designed to have the same orbital period around the Sun as the Earth, The Helios spacecraft have a shorter orbit. But like Helios the orbit would be (close to) elliptical around the Sun rather than circular.

“Quasi-satellites are co-orbital objects that librate around 0° from the primary. Low-eccentricity quasi-satellite orbits are highly unstable, but for moderate to high eccentricities such orbits can be stable. From a co-rotating perspective the quasi-satellite appears to orbit the primary like a retrograde satellite.”

That’s what I’m talking about, unless they’re ignoring the inclination. Checking reference: “we assume that both planets share the same orbital plane” ie. inclination zero. Darn it that’s useless, I’d already figured out the approximate maths for that 30 years ago.

> 3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides.

It has to work.

For every inclination there is an eccentricity that gives a quasi-circular 1:1 resonant orbit about the Earth when viewed along the Earth-Sun axis. It’s easier to calculate the other way around – given an eccentricity calculate an inclination. For mild inclinations the eccentricity increases with inclination. For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations. I’m not al all interested in orbital inclinations exceeding 45 degrees.

The simplest calculation method requires Kepler’s third law, equal arc areas in equal times. The simplest approximation replaces the ellipse with an offset circle (Copernicus’s approximation), which works for small eccentricities. But I might be able to go full ellipse in Excel.

I’ve been making calculation errors lately, let’s hope I don’t stuff this one up.

For even better vision, make the orbit quasi-elliptical (around the centre not the focal point) when viewed along the Earth-Sun axis to give the same zodiacal light seeing conditions in the ecliptic plane and off the ecliptic plane. The calculation is not – in principle – more difficult.

I know what you’re asking yourself. The Earth’s orbit isn’t perfectly circular. Does this make things harder or easier. Easier, in the sense that it allows the spacecraft orbit to be more circular, although it fixes the axis of the inclination to be parallel to the minor axis of the Earth’s ellipse. For easy of calculation, ignore the Earth’s eccentricity of orbit.

> For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations.

Um, no. For 90 degree inclination the orbit viewed along the Earth-Sun axis is close to a semicircle, not a full circle. The semicircle is traversed backwards an forwards once each year. Ignore that strategy for small inclinations.

Compare the above image of brightness of zodiacal light with the below image of pseudo-elliptical orbit of space telescope around Sun with semi-major axis 1.05, eccentricity 0.426, orbital inclination 45 degrees. Orbit around Sun is as viewed along Earth-Sun axis, to make it look like an orbit around the Earth. Not too bad, actually.

Same, but pseudo-circular orbit with semi-major axis 1.025, eccentricity 0.3085, orbital inclination 45 degrees.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

> 3. A polar orbit around the Earth way bigger than the Moon’s orbit. The orbital axis points at the Sun so the spacecraft always looks past the Sun – on all sides.

It has to work.

For every inclination there is an eccentricity that gives a quasi-circular 1:1 resonant orbit about the Earth when viewed along the Earth-Sun axis. It’s easier to calculate the other way around – given an eccentricity calculate an inclination. For mild inclinations the eccentricity increases with inclination. For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations. I’m not al all interested in orbital inclinations exceeding 45 degrees.

The simplest calculation method requires Kepler’s third law, equal arc areas in equal times. The simplest approximation replaces the ellipse with an offset circle (Copernicus’s approximation), which works for small eccentricities. But I might be able to go full ellipse in Excel.

I’ve been making calculation errors lately, let’s hope I don’t stuff this one up.

For even better vision, make the orbit quasi-elliptical (around the centre not the focal point) when viewed along the Earth-Sun axis to give the same zodiacal light seeing conditions in the ecliptic plane and off the ecliptic plane. The calculation is not – in principle – more difficult.

I know what you’re asking yourself. The Earth’s orbit isn’t perfectly circular. Does this make things harder or easier. Easier, in the sense that it allows the spacecraft orbit to be more circular, although it fixes the axis of the inclination to be parallel to the minor axis of the Earth’s ellipse. For easy of calculation, ignore the Earth’s eccentricity of orbit.

> For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations.

Um, no. For 90 degree inclination the orbit viewed along the Earth-Sun axis is close to a semicircle, not a full circle. The semicircle is traversed backwards an forwards once each year. Ignore that strategy for small inclinations.

Compare the above image of brightness of zodiacal light with the below image of pseudo-elliptical orbit of space telescope around Sun with semi-major axis 1.05, eccentricity 0.426, orbital inclination 45 degrees. Orbit around Sun is as viewed along Earth-Sun axis, to make it look like an orbit around the Earth. Not too bad, actually.

Same, but pseudo-circular orbit with semi-major axis 1.025, eccentricity 0.3085, orbital inclination 45 degrees.

Direct comparison of mollwollfumble’s new patent pending (TIC) ellipse-like satellite orbits with the inner zodiacal light contours. The shape is no longer the same (oh well, you win some you lose some) because I’ve switched between plotting tan theta and plotting theta directly. “a” is semi-major-axis length relative to Earth’s 1 AU. Angles in degrees.

“a” controls the side to side width of the orbit. The orbital inclination “i” controls the top to bottom width of the orbit.

The L4 and L5 Lagrangian points are +60 and -60 degrees on the x axis, 0 degrees on the y axis.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

I know what you’re asking yourself. The Earth’s orbit isn’t perfectly circular. Does this make things harder or easier. Easier, in the sense that it allows the spacecraft orbit to be more circular, although it fixes the axis of the inclination to be parallel to the minor axis of the Earth’s ellipse. For easy of calculation, ignore the Earth’s eccentricity of orbit.

> For an extreme 90 degree inclination a circular orbit will again suffice, though using a different strategy. That suggests that there may be multiple strategies at intermediate inclinations.

Um, no. For 90 degree inclination the orbit viewed along the Earth-Sun axis is close to a semicircle, not a full circle. The semicircle is traversed backwards an forwards once each year. Ignore that strategy for small inclinations.

Compare the above image of brightness of zodiacal light with the below image of pseudo-elliptical orbit of space telescope around Sun with semi-major axis 1.05, eccentricity 0.426, orbital inclination 45 degrees. Orbit around Sun is as viewed along Earth-Sun axis, to make it look like an orbit around the Earth. Not too bad, actually.

Same, but pseudo-circular orbit with semi-major axis 1.025, eccentricity 0.3085, orbital inclination 45 degrees.

Direct comparison of mollwollfumble’s new patent pending (TIC) ellipse-like satellite orbits with the inner zodiacal light contours. The shape is no longer the same (oh well, you win some you lose some) because I’ve switched between plotting tan theta and plotting theta directly. “a” is semi-major-axis length relative to Earth’s 1 AU. Angles in degrees.

“a” controls the side to side width of the orbit. The orbital inclination “i” controls the top to bottom width of the orbit.

The L4 and L5 Lagrangian points are +60 and -60 degrees on the x axis, 0 degrees on the y axis.

I should not use a=1.05, 1.025, 1.01 in that figure. Those are quite wong. I included it to show that these orbits are not hugely different from circular.

I should have said flattening (minor axis on major axis) is 0.9, 0.95, 0.98. These correspond to ellipticities of 0.426, 0.3085, 0.198, remembering that circle has ellipticity zero.

Are these orbits unconditionally stable? Probably not, but I’d be prepared to bet real money that slight variations on these can be made stable for a hundred years or more, long enough for a space telescope project. Why? Because although these orbits are calculated heliocentric with just two bodies, they resemble Earth orbits, so a linear interpolation of the heliocentric orbit and the most similar Earth orbit should be close to stable.

The lateral position of the Earth within the heliocentric orbit is arbitrary so, rather than placing the Earth at the centre of the quasi-ellipse, a more stable orbit would have the Earth offset towards one of the foci of the quasi-ellipse. A little unfortunate as regards seeing past the zodiacal light, but there would be no offset required for stability for a quasi-circular orbit, and having no offset would be stable enough as is.

Ooh ahh.

The most stable orbit of all would be one in which the major axis of the ellipse is vertical rather than horizontal. That way the Earth could be placed at the focus without any horizontal offset. I’m itching to know how stable it would be, perhaps very close to unconditionally stable.

I wonder if there’s an orbit expert I could ask.

But it’s not ideal for viewing past the zodiacal light, because the zodiacal light has major axis horizontal.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Compare the above image of brightness of zodiacal light with the below image of pseudo-elliptical orbit of space telescope around Sun with semi-major axis 1.05, eccentricity 0.426, orbital inclination 45 degrees. Orbit around Sun is as viewed along Earth-Sun axis, to make it look like an orbit around the Earth. Not too bad, actually.

Same, but pseudo-circular orbit with semi-major axis 1.025, eccentricity 0.3085, orbital inclination 45 degrees.

Direct comparison of mollwollfumble’s new patent pending (TIC) ellipse-like satellite orbits with the inner zodiacal light contours. The shape is no longer the same (oh well, you win some you lose some) because I’ve switched between plotting tan theta and plotting theta directly. “a” is semi-major-axis length relative to Earth’s 1 AU. Angles in degrees.

“a” controls the side to side width of the orbit. The orbital inclination “i” controls the top to bottom width of the orbit.

The L4 and L5 Lagrangian points are +60 and -60 degrees on the x axis, 0 degrees on the y axis.

I should not use a=1.05, 1.025, 1.01 in that figure. Those are quite wong. I included it to show that these orbits are not hugely different from circular.

I should have said flattening (minor axis on major axis) is 0.9, 0.95, 0.98. These correspond to ellipticities of 0.426, 0.3085, 0.198, remembering that circle has ellipticity zero.

Are these orbits unconditionally stable? Probably not, but I’d be prepared to bet real money that slight variations on these can be made stable for a hundred years or more, long enough for a space telescope project. Why? Because although these orbits are calculated heliocentric with just two bodies, they resemble Earth orbits, so a linear interpolation of the heliocentric orbit and the most similar Earth orbit should be close to stable.

The lateral position of the Earth within the heliocentric orbit is arbitrary so, rather than placing the Earth at the centre of the quasi-ellipse, a more stable orbit would have the Earth offset towards one of the foci of the quasi-ellipse. A little unfortunate as regards seeing past the zodiacal light, but there would be no offset required for stability for a quasi-circular orbit, and having no offset would be stable enough as is.

Ooh ahh.

The most stable orbit of all would be one in which the major axis of the ellipse is vertical rather than horizontal. That way the Earth could be placed at the focus without any horizontal offset. I’m itching to know how stable it would be, perhaps very close to unconditionally stable.

I wonder if there’s an orbit expert I could ask.

But it’s not ideal for viewing past the zodiacal light, because the zodiacal light has major axis horizontal.

Let’s try this.

https://sci-hub.tw/https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506

> Coorbital Dynamics at Large Eccentricity and Inclination

> We show that coorbital dynamics at large eccentricity and inclination exhibit hitherto unknown types of stable motion in the gravitational three-body problem.

Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

But they only look at extremely few combinations of eccentricity and inclination, specifically these four cases:

• e = i = 0
• e = 0.4, i = 0
• e = 0.3, I = 20 deg
• e = 0.5, i = 30 deg

Nor do they acknowledge unstable equilibrium (eg. L1, L2 and L3) which suffice for real satellites.

On the other hand, they do say that retrograde orbits around the Sun are unconditionally stable in the last three cases.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Direct comparison of mollwollfumble’s new patent pending (TIC) ellipse-like satellite orbits with the inner zodiacal light contours. The shape is no longer the same (oh well, you win some you lose some) because I’ve switched between plotting tan theta and plotting theta directly. “a” is semi-major-axis length relative to Earth’s 1 AU. Angles in degrees.

“a” controls the side to side width of the orbit. The orbital inclination “i” controls the top to bottom width of the orbit.

The L4 and L5 Lagrangian points are +60 and -60 degrees on the x axis, 0 degrees on the y axis.

I should not use a=1.05, 1.025, 1.01 in that figure. Those are quite wong. I included it to show that these orbits are not hugely different from circular.

I should have said flattening (minor axis on major axis) is 0.9, 0.95, 0.98. These correspond to ellipticities of 0.426, 0.3085, 0.198, remembering that circle has ellipticity zero.

Are these orbits unconditionally stable? Probably not, but I’d be prepared to bet real money that slight variations on these can be made stable for a hundred years or more, long enough for a space telescope project. Why? Because although these orbits are calculated heliocentric with just two bodies, they resemble Earth orbits, so a linear interpolation of the heliocentric orbit and the most similar Earth orbit should be close to stable.

The lateral position of the Earth within the heliocentric orbit is arbitrary so, rather than placing the Earth at the centre of the quasi-ellipse, a more stable orbit would have the Earth offset towards one of the foci of the quasi-ellipse. A little unfortunate as regards seeing past the zodiacal light, but there would be no offset required for stability for a quasi-circular orbit, and having no offset would be stable enough as is.

Ooh ahh.

The most stable orbit of all would be one in which the major axis of the ellipse is vertical rather than horizontal. That way the Earth could be placed at the focus without any horizontal offset. I’m itching to know how stable it would be, perhaps very close to unconditionally stable.

I wonder if there’s an orbit expert I could ask.

But it’s not ideal for viewing past the zodiacal light, because the zodiacal light has major axis horizontal.

Let’s try this.

https://sci-hub.tw/https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506

> Coorbital Dynamics at Large Eccentricity and Inclination

> We show that coorbital dynamics at large eccentricity and inclination exhibit hitherto unknown types of stable motion in the gravitational three-body problem.

Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

But they only look at extremely few combinations of eccentricity and inclination, specifically these four cases:

• e = i = 0
• e = 0.4, i = 0
• e = 0.3, I = 20 deg
• e = 0.5, i = 30 deg

Nor do they acknowledge unstable equilibrium (eg. L1, L2 and L3) which suffice for real satellites.

On the other hand, they do say that retrograde orbits around the Sun are unconditionally stable in the last three cases.

> Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

Yes it is included! They call the mollwollfumble patent-pending orbit a retrograde orbit because even though it is prograde around the Sun, it appears retrograde around the Earth, when viewed from the north ecliptic pole. It’s the orbit marked RS on this figure. Earth is at angle zero, so this orbit is way closer to Earth than the Lagrangian point orbits marked T. Why they consider the orbit to be RS is beyond me.

So these orbits are known. Good.

I have nutted out an approximate relationship between maximum stability and heliocentric orbit inclination. The result looks like this.

This curve is not particularly reliable as I’ve used, among other approximations, the assumption that tan(theta) is approximately equal to theta, which is way out for inclination angles of 45 degrees and above.

Not that this is the approximate locus of maximum stability, not the best seeing around the inner zodiacal light. Orbits with better seeing around the inner zodiacal light have higher eccentricity.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

I should not use a=1.05, 1.025, 1.01 in that figure. Those are quite wong. I included it to show that these orbits are not hugely different from circular.

I should have said flattening (minor axis on major axis) is 0.9, 0.95, 0.98. These correspond to ellipticities of 0.426, 0.3085, 0.198, remembering that circle has ellipticity zero.

Are these orbits unconditionally stable? Probably not, but I’d be prepared to bet real money that slight variations on these can be made stable for a hundred years or more, long enough for a space telescope project. Why? Because although these orbits are calculated heliocentric with just two bodies, they resemble Earth orbits, so a linear interpolation of the heliocentric orbit and the most similar Earth orbit should be close to stable.

The lateral position of the Earth within the heliocentric orbit is arbitrary so, rather than placing the Earth at the centre of the quasi-ellipse, a more stable orbit would have the Earth offset towards one of the foci of the quasi-ellipse. A little unfortunate as regards seeing past the zodiacal light, but there would be no offset required for stability for a quasi-circular orbit, and having no offset would be stable enough as is.

Ooh ahh.

The most stable orbit of all would be one in which the major axis of the ellipse is vertical rather than horizontal. That way the Earth could be placed at the focus without any horizontal offset. I’m itching to know how stable it would be, perhaps very close to unconditionally stable.

I wonder if there’s an orbit expert I could ask.

But it’s not ideal for viewing past the zodiacal light, because the zodiacal light has major axis horizontal.

Let’s try this.

https://sci-hub.tw/https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506

> Coorbital Dynamics at Large Eccentricity and Inclination

> We show that coorbital dynamics at large eccentricity and inclination exhibit hitherto unknown types of stable motion in the gravitational three-body problem.

Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

But they only look at extremely few combinations of eccentricity and inclination, specifically these four cases:

• e = i = 0
• e = 0.4, i = 0
• e = 0.3, I = 20 deg
• e = 0.5, i = 30 deg

Nor do they acknowledge unstable equilibrium (eg. L1, L2 and L3) which suffice for real satellites.

On the other hand, they do say that retrograde orbits around the Sun are unconditionally stable in the last three cases.

> Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

Yes it is included! They call the mollwollfumble patent-pending orbit a retrograde orbit because even though it is prograde around the Sun, it appears retrograde around the Earth, when viewed from the north ecliptic pole. It’s the orbit marked RS on this figure. Earth is at angle zero, so this orbit is way closer to Earth than the Lagrangian point orbits marked T. Why they consider the orbit to be RS is beyond me.

So these orbits are known. Good.

I have nutted out an approximate relationship between maximum stability and heliocentric orbit inclination. The result looks like this.

This curve is not particularly reliable as I’ve used, among other approximations, the assumption that tan(theta) is approximately equal to theta, which is way out for inclination angles of 45 degrees and above.

Not that this is the approximate locus of maximum stability, not the best seeing around the inner zodiacal light. Orbits with better seeing around the inner zodiacal light have higher eccentricity.

Posted the following question on Physics forum.

Information wanted on three-body solvers, and on high inclination coorbitals

I was working on a proposal for a spacecraft, and suddenly realised that the ideal orbit may be a high inclination type of near-Earth coorbital called a “retrograde satellite” or RS orbit. Do you know of:

• A person who can compute 100 years of coorbital stability using three body (sun, earth, satellite) or four body (with moon) kinematics?
• A simple-to-use approximate 3-D calculator for the three body problem, simplified so the third body has negligible mass.
• Where I can find as much information as possible on RS orbits in general. eg. ellipticity vs inclination.
• Any information at all on periodic RS orbits with 1:1 resonance.

So far, all I know about RS orbits comes from “Coorbital Dynamics at Large Eccentricity and Inclination “, https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506
The inclination range I’m most interested in is 15 to 45 degrees.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Let’s try this.

https://sci-hub.tw/https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506

> Coorbital Dynamics at Large Eccentricity and Inclination

> We show that coorbital dynamics at large eccentricity and inclination exhibit hitherto unknown types of stable motion in the gravitational three-body problem.

Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

But they only look at extremely few combinations of eccentricity and inclination, specifically these four cases:

• e = i = 0
• e = 0.4, i = 0
• e = 0.3, I = 20 deg
• e = 0.5, i = 30 deg

Nor do they acknowledge unstable equilibrium (eg. L1, L2 and L3) which suffice for real satellites.

On the other hand, they do say that retrograde orbits around the Sun are unconditionally stable in the last three cases.

> Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

Yes it is included! They call the mollwollfumble patent-pending orbit a retrograde orbit because even though it is prograde around the Sun, it appears retrograde around the Earth, when viewed from the north ecliptic pole. It’s the orbit marked RS on this figure. Earth is at angle zero, so this orbit is way closer to Earth than the Lagrangian point orbits marked T. Why they consider the orbit to be RS is beyond me.

So these orbits are known. Good.

I have nutted out an approximate relationship between maximum stability and heliocentric orbit inclination. The result looks like this.

This curve is not particularly reliable as I’ve used, among other approximations, the assumption that tan(theta) is approximately equal to theta, which is way out for inclination angles of 45 degrees and above.

Not that this is the approximate locus of maximum stability, not the best seeing around the inner zodiacal light. Orbits with better seeing around the inner zodiacal light have higher eccentricity.

Posted the following question on Physics forum.

Information wanted on three-body solvers, and on high inclination coorbitals

I was working on a proposal for a spacecraft, and suddenly realised that the ideal orbit may be a high inclination type of near-Earth coorbital called a “retrograde satellite” or RS orbit. Do you know of:

• A person who can compute 100 years of coorbital stability using three body (sun, earth, satellite) or four body (with moon) kinematics?
• A simple-to-use approximate 3-D calculator for the three body problem, simplified so the third body has negligible mass.
• Where I can find as much information as possible on RS orbits in general. eg. ellipticity vs inclination.
• Any information at all on periodic RS orbits with 1:1 resonance.

So far, all I know about RS orbits comes from “Coorbital Dynamics at Large Eccentricity and Inclination “, https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506
The inclination range I’m most interested in is 15 to 45 degrees.

This figure seems to suggest that for the 15 to 45 degrees I’m interested in, a whole range of eccentricities (0.35 to 0.99) are OK, dark symbols. But their criterion for OK, libration amplitude less than 50 degrees, is way too lax. I want a libration amplitude of zero, ie. a periodic orbit.

From A numerical investigation of coorbital stability and libration in three dimensions

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

> Hmm, going by their Figure 1 (their only Figure), the type of orbit I’m proposing isn’t included as any of the stable ones.

Yes it is included! They call the mollwollfumble patent-pending orbit a retrograde orbit because even though it is prograde around the Sun, it appears retrograde around the Earth, when viewed from the north ecliptic pole. It’s the orbit marked RS on this figure. Earth is at angle zero, so this orbit is way closer to Earth than the Lagrangian point orbits marked T. Why they consider the orbit to be RS is beyond me.

So these orbits are known. Good.

I have nutted out an approximate relationship between maximum stability and heliocentric orbit inclination. The result looks like this.

This curve is not particularly reliable as I’ve used, among other approximations, the assumption that tan(theta) is approximately equal to theta, which is way out for inclination angles of 45 degrees and above.

Not that this is the approximate locus of maximum stability, not the best seeing around the inner zodiacal light. Orbits with better seeing around the inner zodiacal light have higher eccentricity.

Posted the following question on Physics forum.

Information wanted on three-body solvers, and on high inclination coorbitals

I was working on a proposal for a spacecraft, and suddenly realised that the ideal orbit may be a high inclination type of near-Earth coorbital called a “retrograde satellite” or RS orbit. Do you know of:

• A person who can compute 100 years of coorbital stability using three body (sun, earth, satellite) or four body (with moon) kinematics?
• A simple-to-use approximate 3-D calculator for the three body problem, simplified so the third body has negligible mass.
• Where I can find as much information as possible on RS orbits in general. eg. ellipticity vs inclination.
• Any information at all on periodic RS orbits with 1:1 resonance.

So far, all I know about RS orbits comes from “Coorbital Dynamics at Large Eccentricity and Inclination “, https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506
The inclination range I’m most interested in is 15 to 45 degrees.

This figure seems to suggest that for the 15 to 45 degrees I’m interested in, a whole range of eccentricities (0.35 to 0.99) are OK, dark symbols. But their criterion for OK, libration amplitude less than 50 degrees, is way too lax. I want a libration amplitude of zero, ie. a periodic orbit.

From A numerical investigation of coorbital stability and libration in three dimensions

Fingers crossed i can use this software for 3-body interactions.

https://ui.adsabs.harvard.edu/link_gateway/2014Icar..231..273G/EPRINT_PDF

Atlas of three body mean motion resonances in the Solar System

We present a numerical method to estimate the strengths of arbitrary three body mean motion resonances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This method allows us to obtain an atlas of the three body resonances in the Solar System showing where are located and how strong are thousands of resonances involving all the planets from 0 to 1000 au.

Code (Fortran 77 yippee) in http://www.fisica.edu.uy/~gallardo/atlas/

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Posted the following question on Physics forum.

Information wanted on three-body solvers, and on high inclination coorbitals

I was working on a proposal for a spacecraft, and suddenly realised that the ideal orbit may be a high inclination type of near-Earth coorbital called a “retrograde satellite” or RS orbit. Do you know of:

• A person who can compute 100 years of coorbital stability using three body (sun, earth, satellite) or four body (with moon) kinematics?
• A simple-to-use approximate 3-D calculator for the three body problem, simplified so the third body has negligible mass.
• Where I can find as much information as possible on RS orbits in general. eg. ellipticity vs inclination.
• Any information at all on periodic RS orbits with 1:1 resonance.

So far, all I know about RS orbits comes from “Coorbital Dynamics at Large Eccentricity and Inclination “, https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.83.2506
The inclination range I’m most interested in is 15 to 45 degrees.

This figure seems to suggest that for the 15 to 45 degrees I’m interested in, a whole range of eccentricities (0.35 to 0.99) are OK, dark symbols. But their criterion for OK, libration amplitude less than 50 degrees, is way too lax. I want a libration amplitude of zero, ie. a periodic orbit.

From A numerical investigation of coorbital stability and libration in three dimensions

Fingers crossed i can use this software for 3-body interactions.

https://ui.adsabs.harvard.edu/link_gateway/2014Icar..231..273G/EPRINT_PDF

Atlas of three body mean motion resonances in the Solar System

We present a numerical method to estimate the strengths of arbitrary three body mean motion resonances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This method allows us to obtain an atlas of the three body resonances in the Solar System showing where are located and how strong are thousands of resonances involving all the planets from 0 to 1000 au.

Code (Fortran 77 yippee) in http://www.fisica.edu.uy/~gallardo/atlas/

How about this?

For each inclination (0.5 degree intervals from 15 to 45 degrees)
For each eccentricity (um, 0.1 to 0.45 by intervals of 0.005)
Calculate apogee radius and speed from heliocentric orbit
Using Newton’s laws, calculate 3-body orbit by integration until next apogee
Adjust (increase slightly) initial speed until final apogee is as close as possible to initial apogee
From final orbit get final eccentricity and min and maximum distance from Earth
Repeat

That way will give me a 2-D map of closeness to a periodic orbit as a function of inclination and apogee radius.

And I can plot maximum distance from Earth vs closeness to a periodic orbit.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

This figure seems to suggest that for the 15 to 45 degrees I’m interested in, a whole range of eccentricities (0.35 to 0.99) are OK, dark symbols. But their criterion for OK, libration amplitude less than 50 degrees, is way too lax. I want a libration amplitude of zero, ie. a periodic orbit.

From A numerical investigation of coorbital stability and libration in three dimensions

Fingers crossed i can use this software for 3-body interactions.

https://ui.adsabs.harvard.edu/link_gateway/2014Icar..231..273G/EPRINT_PDF

Atlas of three body mean motion resonances in the Solar System

We present a numerical method to estimate the strengths of arbitrary three body mean motion resonances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This method allows us to obtain an atlas of the three body resonances in the Solar System showing where are located and how strong are thousands of resonances involving all the planets from 0 to 1000 au.

Code (Fortran 77 yippee) in http://www.fisica.edu.uy/~gallardo/atlas/

How about this?

For each inclination (0.5 degree intervals from 15 to 45 degrees)
For each eccentricity (um, 0.1 to 0.45 by intervals of 0.005)
Calculate apogee radius and speed from heliocentric orbit
Using Newton’s laws, calculate 3-body orbit by integration until next apogee
Adjust (increase slightly) initial speed until final apogee is as close as possible to initial apogee
From final orbit get final eccentricity and min and maximum distance from Earth
Repeat

That way will give me a 2-D map of closeness to a periodic orbit as a function of inclination and apogee radius.

And I can plot maximum distance from Earth vs closeness to a periodic orbit.

This is quite pretty, I just calculated this. See the gap in this orbit. That’s the influence that Earth’s gravity has on the heliocentric “reverse satellite” coorbital I just calculated. If the Earth’s gravity was missing from the calculation, there would be no gap (PS, will try this). By subtly and iteratively changing the initial velocity I want to close that gap as precisely as possible. When the gap is closed, that will give a coorbital with a period of exactly a year, but there will still be a teeny error in either velicuity or radius – and that will give me the stability of the coorbital.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Fingers crossed i can use this software for 3-body interactions.

https://ui.adsabs.harvard.edu/link_gateway/2014Icar..231..273G/EPRINT_PDF

Atlas of three body mean motion resonances in the Solar System

We present a numerical method to estimate the strengths of arbitrary three body mean motion resonances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This method allows us to obtain an atlas of the three body resonances in the Solar System showing where are located and how strong are thousands of resonances involving all the planets from 0 to 1000 au.

Code (Fortran 77 yippee) in http://www.fisica.edu.uy/~gallardo/atlas/

How about this?

For each inclination (0.5 degree intervals from 15 to 45 degrees)
For each eccentricity (um, 0.1 to 0.45 by intervals of 0.005)
Calculate apogee radius and speed from heliocentric orbit
Using Newton’s laws, calculate 3-body orbit by integration until next apogee
Adjust (increase slightly) initial speed until final apogee is as close as possible to initial apogee
From final orbit get final eccentricity and min and maximum distance from Earth
Repeat

That way will give me a 2-D map of closeness to a periodic orbit as a function of inclination and apogee radius.

And I can plot maximum distance from Earth vs closeness to a periodic orbit.

This is quite pretty, I just calculated this. See the gap in this orbit. That’s the influence that Earth’s gravity has on the heliocentric “reverse satellite” coorbital I just calculated. If the Earth’s gravity was missing from the calculation, there would be no gap (PS, will try this). By subtly and iteratively changing the initial velocity I want to close that gap as precisely as possible. When the gap is closed, that will give a coorbital with a period of exactly a year, but there will still be a teeny error in either velicuity or radius – and that will give me the stability of the coorbital.

Oops, programming bug. The closure error on the orbit (numerical error) is now the Earth’s diameter, 12,000 km, over a distance of the perimeter of the Earth’s orbit, about 10,000,000 km. Error one part in 1,000. That’s actually too small to see on any plot. But I want to see if I can get it even better.