Direct continuation from:

https://tokyo3.org/forums/holiday/topics/12088/

mollwollfumble said:

mollwollfumble said:

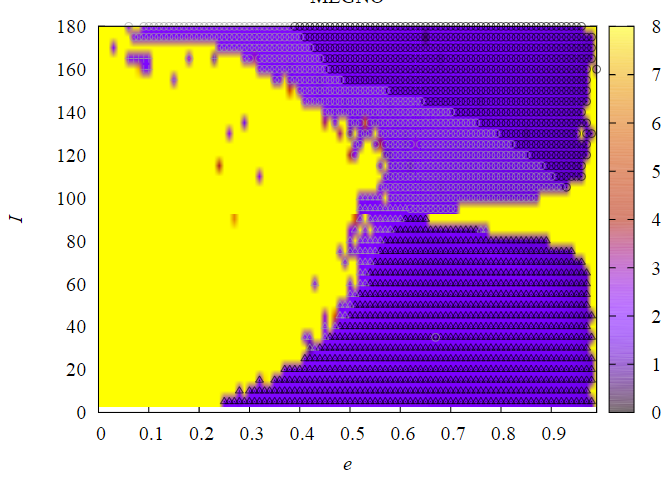
mollwollfumble said:

This figure seems to suggest that for the 15 to 45 degrees I’m interested in, a whole range of eccentricities (0.35 to 0.99) are OK, dark symbols. But their criterion for OK, libration amplitude less than 50 degrees, is way too lax. I want a libration amplitude of zero, ie. a periodic orbit.

From A numerical investigation of coorbital stability and libration in three dimensions

Fingers crossed i can use this software for 3-body interactions.

https://ui.adsabs.harvard.edu/link_gateway/2014Icar..231..273G/EPRINT_PDF

Atlas of three body mean motion resonances in the Solar System

We present a numerical method to estimate the strengths of arbitrary three body mean motion resonances between two planets in circular coplanar orbits and a massless particle in an arbitrary orbit. This method allows us to obtain an atlas of the three body resonances in the Solar System showing where are located and how strong are thousands of resonances involving all the planets from 0 to 1000 au.

Code (Fortran 77 yippee) in http://www.fisica.edu.uy/~gallardo/atlas/

How about this?

For each inclination (0.5 degree intervals from 15 to 45 degrees)
For each eccentricity (um, 0.1 to 0.45 by intervals of 0.005)
Calculate apogee radius and speed from heliocentric orbit
Using Newton’s laws, calculate 3-body orbit by integration until next apogee
Adjust (increase slightly) initial speed until final apogee is as close as possible to initial apogee
From final orbit get final eccentricity and min and maximum distance from Earth
Repeat

That way will give me a 2-D map of closeness to a periodic orbit as a function of inclination and apogee radius.

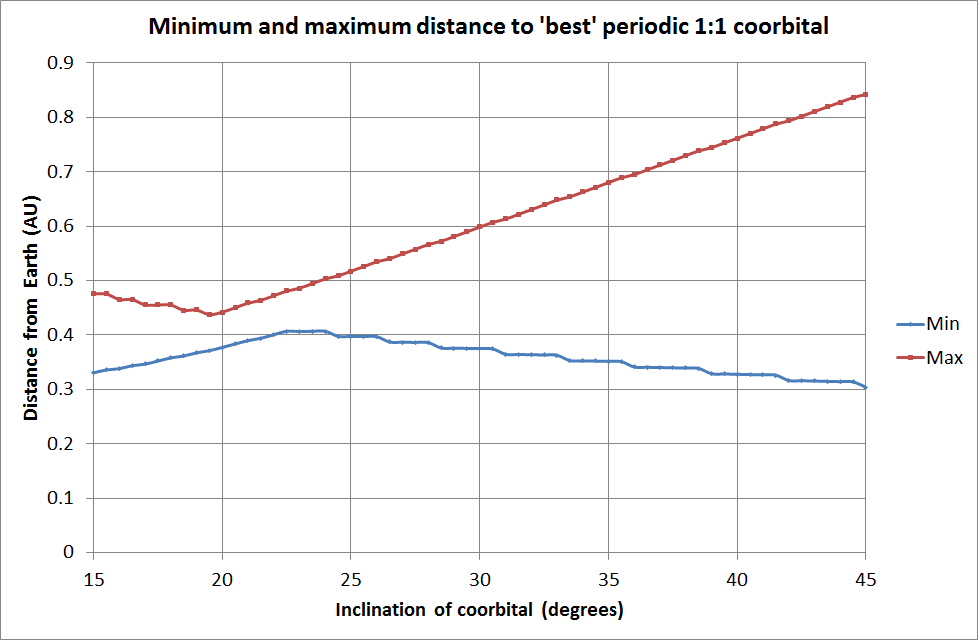
And I can plot maximum distance from Earth vs closeness to a periodic orbit.

Worked better than I would have believed possible. I was prepared to accept a lack of orbit closure in the ballpark of 10,000 km per year (one Earth diameter) as acceptable. I’m getting a periodic orbit closure error of order 1 km per year! And a periodic orbit velocity closure of order only 1 m/s per year. Amazing.

Even better, there is a unique best eccentricity of orbit for each inclination.

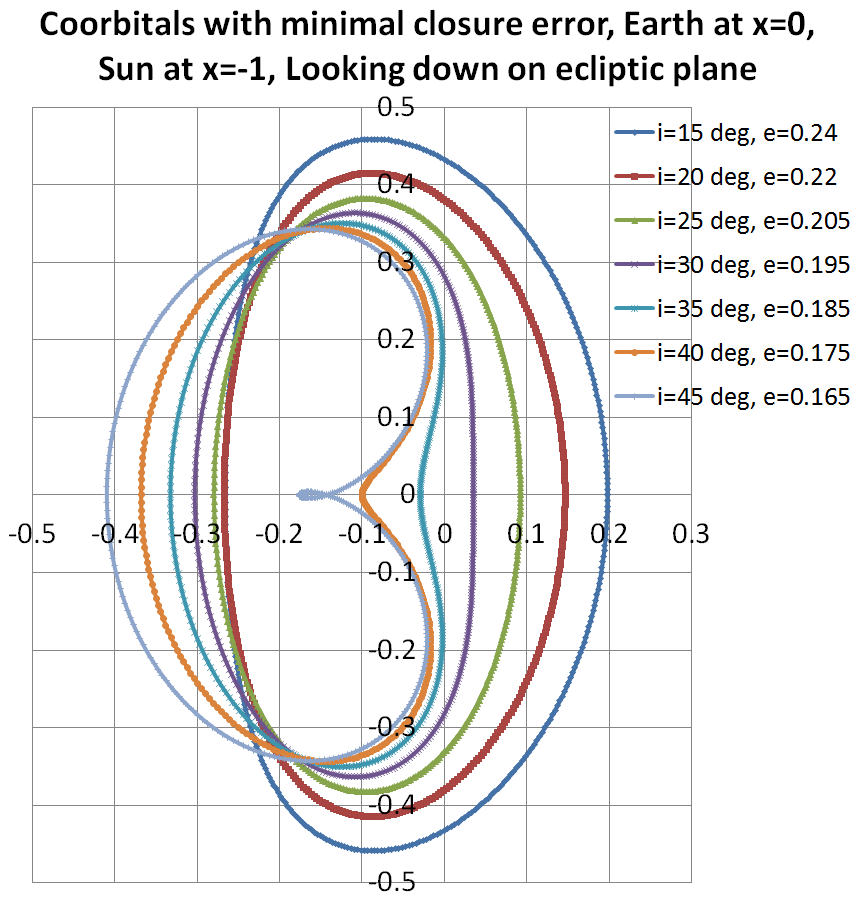
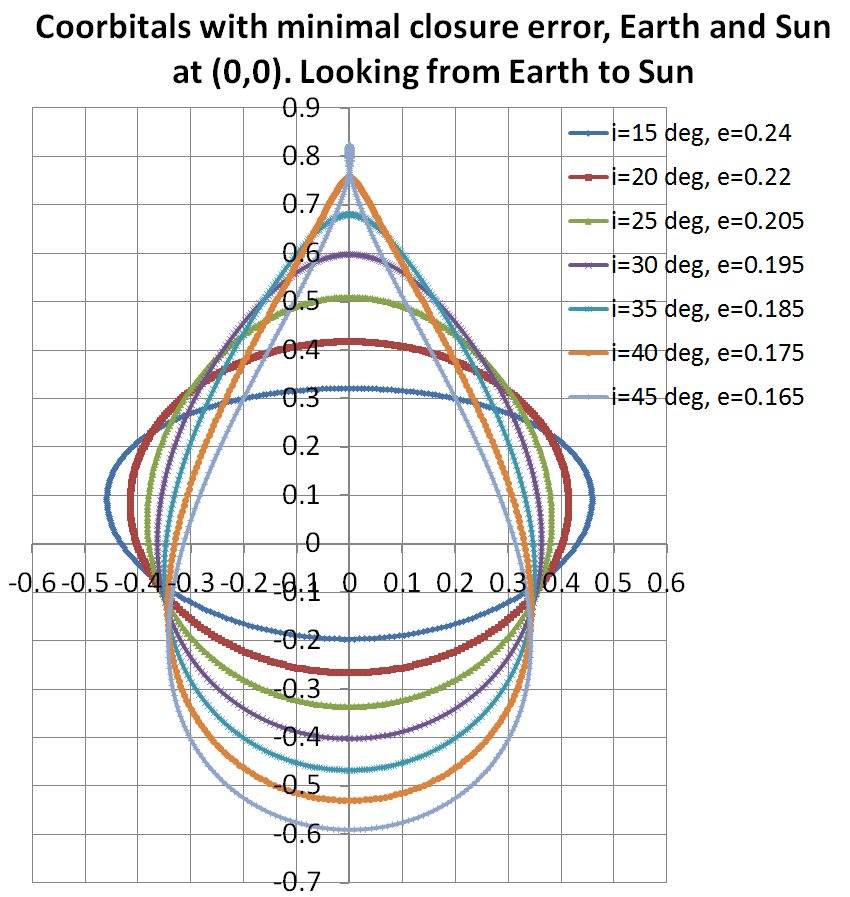
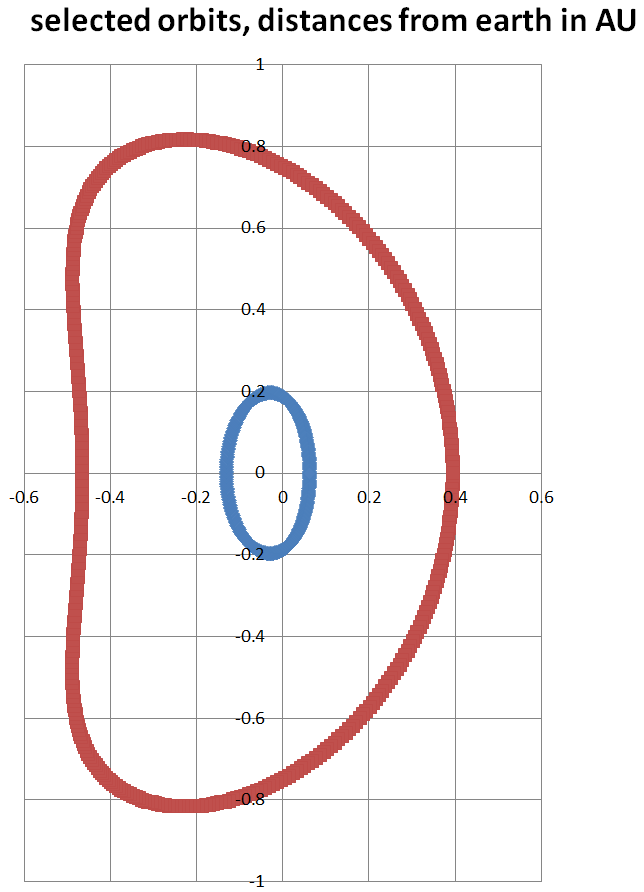
Typical orbits, as viewed looking down on the plane of the ecliptic. Earth is at (0,0). Smaller orbits are like a squashed ellipse. Larger orbits are jelly-bean shape in this view, with horns pointed towards the 60 degree Lagrangian points.

Smaller orbits have the advantage of faster Earth-satellite communications. Larger orbits have the advantage of better view past the inner zodiacal light.

Error or orbit closeuse, as a function of ellipticity and inclination (15 to 45 degrees inclination). There’s a unique best eccentricity for each inclination, and even a lack of closure of 30 km is very small.

Locus of best eccentricity at each inclination.

did the other thread run out of space?

Arts said:

did the other thread run out of space?

Maybe it was de-lighted.

Arts said:

did the other thread run out of space?

The prediction told him to start a new thread.

“Due to inner conflict start a new thread, what out for the number 3 and you will come into money but then get hit by a bus picking it up”

Zodiacal light is often mistaken for an aurora.

Bubblecar said:

Zodiacal light is often mistaken for an aurora.

That’s a point.

Other thread got so far back on both “view by thread” and “view by time” that it was becoming hard to find.

I expected weird, but not quite this weird. Coorbital RS orbits, 1:1 resonant with Earth, with maximal (very good) stability. They don’t look like elliptic orbits with focus at (0,0). The negative x values are because we’re looking at down on orbits inclined by up to 45 degrees from the ecliptic.

On this chart, the L4, L5 lagrangian points would appear at (-0.5, ±0.866). So these orbits are all much closer than orbits around the Lagrangian points.

mollwollfumble said:

Bubblecar said:

Zodiacal light is often mistaken for an aurora.

That’s a point.

Other thread got so far back on both “view by thread” and “view by time” that it was becoming hard to find.

I expected weird, but not quite this weird. Coorbital RS orbits, 1:1 resonant with Earth, with maximal (very good) stability. They don’t look like elliptic orbits with focus at (0,0). The negative x values are because we’re looking at down on orbits inclined by up to 45 degrees from the ecliptic.

On this chart, the L4, L5 lagrangian points would appear at (-0.5, ±0.866). So these orbits are all much closer than orbits around the Lagrangian points.

Inclination 20 degrees (or 19.5 degrees) and eccentricity 0.22 is just about damn perfect.

• 1:1 periodic orbit with minimal error in orbit closure.
• smallest maximum distance from Earth for a minimal error orbit, makes communications as good as possible.
• the right shape to avoid the inner Zodiacal light – wide when crossing the ecliptic and narrower off the ecliptic, and far enough away to avoid the innermost parts.

Smallest maximum distance from Earth. The distance from Earth to the L4/L5 Lagrangian points is 1.

Right shape to avoid inner zodiacal light. The zodiacal light is most concentrated on the ecliptic, which is the axis y=0 in the following figure.

mollwollfumble said:

mollwollfumble said:

Bubblecar said:

Zodiacal light is often mistaken for an aurora.

That’s a point.

Other thread got so far back on both “view by thread” and “view by time” that it was becoming hard to find.

I expected weird, but not quite this weird. Coorbital RS orbits, 1:1 resonant with Earth, with maximal (very good) stability. They don’t look like elliptic orbits with focus at (0,0). The negative x values are because we’re looking at down on orbits inclined by up to 45 degrees from the ecliptic.

On this chart, the L4, L5 lagrangian points would appear at (-0.5, ±0.866). So these orbits are all much closer than orbits around the Lagrangian points.

Inclination 20 degrees (or 19.5 degrees) and eccentricity 0.22 is just about damn perfect.

• 1:1 periodic orbit with minimal error in orbit closure.
• smallest maximum distance from Earth for a minimal error orbit, makes communications as good as possible.
• the right shape to avoid the inner Zodiacal light – wide when crossing the ecliptic and narrower off the ecliptic, and far enough away to avoid the innermost parts.

Smallest maximum distance from Earth. The distance from Earth to the L4/L5 Lagrangian points is 1.

Right shape to avoid inner zodiacal light. The zodiacal light is most concentrated on the ecliptic, which is the axis y=0 in the following figure.

So are you sending this research to the relevant agencies?

Bubblecar said:

mollwollfumble said:

mollwollfumble said:

That’s a point.

Other thread got so far back on both “view by thread” and “view by time” that it was becoming hard to find.

I expected weird, but not quite this weird. Coorbital RS orbits, 1:1 resonant with Earth, with maximal (very good) stability. They don’t look like elliptic orbits with focus at (0,0). The negative x values are because we’re looking at down on orbits inclined by up to 45 degrees from the ecliptic.

On this chart, the L4, L5 lagrangian points would appear at (-0.5, ±0.866). So these orbits are all much closer than orbits around the Lagrangian points.

Inclination 20 degrees (or 19.5 degrees) and eccentricity 0.22 is just about damn perfect.

• 1:1 periodic orbit with minimal error in orbit closure.
• smallest maximum distance from Earth for a minimal error orbit, makes communications as good as possible.
• the right shape to avoid the inner Zodiacal light – wide when crossing the ecliptic and narrower off the ecliptic, and far enough away to avoid the innermost parts.

Smallest maximum distance from Earth. The distance from Earth to the L4/L5 Lagrangian points is 1.

Right shape to avoid inner zodiacal light. The zodiacal light is most concentrated on the ecliptic, which is the axis y=0 in the following figure.

So are you sending this research to the relevant agencies?

I want to. I plan to. Am i too chicken? Cluck, cluck.

Just spent a freaking hour and a half backing up to Word the thread:

https://tokyo3.org/forums/holiday/topics/12088/

Bubblecar said:

So are you sending this research to the relevant agencies?

Have submitted to ESA.