I’ve been shuffling drink coasters lately, which got me wondering – is stacking a deck of cards like solving Rubik’s cube?

Similarities would be:

• It takes a lot of practice to become dextrous at it – fast and accurate
• There are a very large number of possible shuffled states, both for the cards and the cube
• It takes about the same number of relatively simple moves in each case
• Each move is cyclic, repeat it exactly often enough and you get back to where you started.

So would that mean that anyone who can solve Rubik’s cube could stack a deck of cards?

Could I figure out, from first principles and a simple computer program, the best way to stack a deck of cards?

Youtube is full of goobers giving tutorials on card manipulation.

https://www.theage.com.au/national/victoria/police-officer-faces-disciplinary-action-over-crude-ead-hippy-sticker-20191101-p536lu.html

Also the sticker was over his camera lens.

A WWI soldier taught me how to stack a deck when I was a kid. It worked on a rhyme that was formed from an acronym for the order of the cards. If your memory was any good, you knew exactly what each player had in his hand.

I forget the rhyme.

Rule 303 said:

A WWI soldier taught me how to stack a deck when I was a kid. It worked on a rhyme that was formed from an acronym for the order of the cards. If your memory was any good, you knew exactly what each player had in his hand.

I forget the rhyme.

And there’s no WW1 soldiers left. :(

I’ve been practicing deck-stacking for years as part of my amateur prestidigitating; I’ve become so good at it that I don’t have to think about it, and do it whenever I shuffle cards. When I’m playing cards with friends and trying to be fair I have to ask someone else to shuffle, because I can’t “turn it off.”

I’ve been doing Rubik’s Cube solving since I was a teenager; while I haven’t done it or practiced it as much as I have deck-stacking, so I’m not as expert, I don’t think of them as the same (although there are similarities.) The two use different forms of dexterity, and I don’t think (though that’s a subjective assessment) either has helped me with the other.

I think these are fairly different

btm said:

I’ve been practicing deck-stacking for years as part of my amateur prestidigitating; I’ve become so good at it that I don’t have to think about it, and do it whenever I shuffle cards. When I’m playing cards with friends and trying to be fair I have to ask someone else to shuffle, because I can’t “turn it off.”

I’ve been doing Rubik’s Cube solving since I was a teenager; while I haven’t done it or practiced it as much as I have deck-stacking, so I’m not as expert, I don’t think of them as the same (although there are similarities.) The two use different forms of dexterity, and I don’t think (though that’s a subjective assessment) either has helped me with the other.

Excellent. Thank you.

Different dexterity, yes, but similar mathematics? I solved the mathematics of Rubik’s cube as a teen, but until now have had zero interest in playing cards.

Looking just at 6 cards, there are 6! = 720 different combinations. A single shuffle can yield (about) 36 results. 36 into 720 is just 20, so only two shuffles, or at most three, would be needed for any combination. For 52 cards, I have no idea what the minimum number of shuffles would be to stack the deck to get any possible combination out of 52! = 10^68 combinations, but I’m guessing it would be less than 26.

Finding the combination for a minimum number of shuffles on the other hand would be next to impossible without a computer, so I’m also guessing that those people who stack the deck only do it for a much smaller number of combinations such as 10^18 combinations using a more restricted gamut of shuffles.

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

The Rev Dodgson said:

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

One shuffles, one cuts

dv said:

The Rev Dodgson said:

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

One shuffles, one cuts

Oh yeah, I knew that once.

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

One shuffles, one cuts

Oh yeah, I knew that once.

Of course if you’re really good then even with a cut, you’ll be able to work out everyone’s hand from your own

dv said:

The Rev Dodgson said:

dv said:

One shuffles, one cuts

Oh yeah, I knew that once.

Of course if you’re really good then even with a cut, you’ll be able to work out everyone’s hand from your own

Is this by using a deck in a specific order before the shuffling and cutting?

Yes

The Rev Dodgson said:

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

Ditto. Also a gigantic hole in my education.

Apart from Bridge tournaments, I don’t know anyone who does play card games with real cards any more. It may be significantly more difficult to stack the deck for Bridge than for Poker. Bridge needs all 52 cards.

Let me start from a position of near-complete ignorance. So please correct what I suggest.

Start with just 10 cards for simplicity, call the initial order 0123456789 with 0 at the top. Total number of permutations is 10! = 3628800

There are three acceptable types of shuffle:
a) The cut eg. 5678901234
b) The pain shuffle eg. 9876543210
c) The riffle shuffle eg. 0246813579

a) The cut. Easiest to control, hardest to cheat on. A cheat on the cut would keep the bottom cards at the bottom, such as 5678012349.

b) The plain shuffle is a set of cuts. But how many cuts? Perhaps aim for in the rough order of ceiling(sqrt(n)) cuts. 3 cuts for 6 cards, 4 cuts for 10 cards, 8 cuts for 52 cards? But what is the acceptable range for the number of cuts? So a typical plain shuffle might be 9784562301. One cheat would be to keep the bottom cards on the bottom such as 8745623019. Then there’s shuffling to the bottom of the deck such as 9876432105. A plain cut always moves a the middle of the deck towards the outside, usually front, and the front of the deck towards the back. Two iterations of 9876543210 take you straight back where you started, 0123456789. For every acceptable plain shuffle, there is a second acceptable(?) plain shuffle that is the exact inverse.

c) I know SFA about riffle shuffles. A perfect riffle shuffle yields either 0246813579 or 1357902468. An imperfect, ie. normal, riffle shuffle is, well, a large number of cuts. How many? A riffle shuffle may be the easiest way to leave the front cards of the deck on the front, (the other way being a pair of plain shuffles).

So stacking could be done on the front of the deck – riffle shuffle, back of the deck – plain shuffle, or both. If both then a single plain shuffle could bring front and back stacks together, such as 012…89 gives either …01289 or …21089 or … 20189 or … 12089 but not (with any ease) the other permutations.

mollwollfumble said:

The Rev Dodgson said:

It seems that deck stacking is a gigantic hole in my education.

If it can be done so reliably and easily by those practiced at it, how come anyone bothers playing card games any more?

Ditto. Also a gigantic hole in my education.

Apart from Bridge tournaments, I don’t know anyone who does play card games with real cards any more. It may be significantly more difficult to stack the deck for Bridge than for Poker. Bridge needs all 52 cards.

Let me start from a position of near-complete ignorance. So please correct what I suggest.

Start with just 10 cards for simplicity, call the initial order 0123456789 with 0 at the top. Total number of permutations is 10! = 3628800

There are three acceptable types of shuffle:
a) The cut eg. 5678901234
b) The pain shuffle eg. 9876543210
c) The riffle shuffle eg. 0246813579

a) The cut. Easiest to control, hardest to cheat on. A cheat on the cut would keep the bottom cards at the bottom, such as 5678012349.

b) The plain shuffle is a set of cuts. But how many cuts? Perhaps aim for in the rough order of ceiling(sqrt(n)) cuts. 3 cuts for 6 cards, 4 cuts for 10 cards, 8 cuts for 52 cards? But what is the acceptable range for the number of cuts? So a typical plain shuffle might be 9784562301. One cheat would be to keep the bottom cards on the bottom such as 8745623019. Then there’s shuffling to the bottom of the deck such as 9876432105. A plain cut always moves a the middle of the deck towards the outside, usually front, and the front of the deck towards the back. Two iterations of 9876543210 take you straight back where you started, 0123456789. For every acceptable plain shuffle, there is a second acceptable(?) plain shuffle that is the exact inverse.

c) I know SFA about riffle shuffles. A perfect riffle shuffle yields either 0246813579 or 1357902468. An imperfect, ie. normal, riffle shuffle is, well, a large number of cuts. How many? A riffle shuffle may be the easiest way to leave the front cards of the deck on the front, (the other way being a pair of plain shuffles).

So stacking could be done on the front of the deck – riffle shuffle, back of the deck – plain shuffle, or both. If both then a single plain shuffle could bring front and back stacks together, such as 012…89 gives either …01289 or …21089 or … 20189 or … 12089 but not (with any ease) the other permutations.

There are a couple of science papers on permutations and cuts.

https://arxiv.org/pdf/1502.07971.pdf

“A simple framework on sorting permutations
Ricky X. F. Chen·Christian M. Reidys
In this paper we present a simple framework to study various distance problems of permutations, including the transposition and block-interchange distance of permutations as well as the reversal distance of signed permutations. These problems are very important in the study of the evolution of genomes.”

LOL, so the mathematics of stacking cards is the same as the mathematics of chromosomal disorders in genomes. I never thought that this was going to end up being a thread about genomes. Note that the “genetic algorithm” works in a bit the same way.

> one-line form: π is represented as a sequence π=π(1)π(2)···π(n−1)π(n).
> cycle form: regarding〈π〉as a cyclic group, we represent π by its collection of orbits (cycles).

That’s part of what i’m looking for. Other paper.

“Information Processing Letters 60 (1996) 165-169
Sorting permutations by block interchanges
David A. Christie”

> In this paper we introduce an operation, called block-interchange, in which two substrings, or blocks, swap positions in the permutation.

That’s four cuts, isn’t it. Any four cuts?

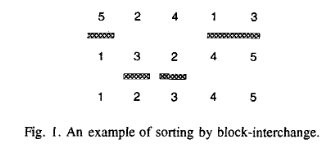
> Lemma 1. It is always possible to find a block-interchange that removes at least two breakpoints (sometimes 3 or 4) from a given permutation, Π unless Π is the identity.

Hmm, this may end up as something bleedin’ obvious, such as saying that every permutation of 52 cards can be generated by 51 cuts.

Almost equally obvious, at most one perfect plain shuffle and 25 cuts will suffice. Because a plain shuffle takes the number of breakpoints from 51. So if the original permutation has 26 breakpoints then a plain shuffle reduces that to 51 – 26 = 25 and each cut removes one of those.

The “block-interchange diameter” BID is the minimum number of block interchanges required to find every permutation. For 52 cards it is 52/2 = 26. So essentially what the article is saying is that 26 cut pairs will suffice to completely stack a set of 52 cards.

Yeah, the result is bleeding’ obvious. The paper does give “The number of permutations of size n that achieve BID” for up to 10 cards in a pack, which is interesting. For 10 cards using block-interchange the number of permutations that require 5 cut-pairs is 604,800. That there is more than 1 is shown by the fact that … I’ll leave that as an exercise for the reader.

10! / 604,800 = 6.
8! / 8,046 = 5.01.
So perhaps with 52 cards the probability that a random deck will have the worst possible BID is near 1/(52/2+1) = 3.7%.

Slightly disappointed. But at least it does mean that stacking cards is a cutting edge problem in applied mathematics.

“evolution of genomes” – I can’t help chuckling.

Hmm, 32-bit computers are capable of storing the complete set of permutations of only a 12 card deck, or only the first three shuffles of a 52 card deck. And even then the storage in both cases exceeds a gigabyte.

Neither is sufficient for extrapolation to a full permutation of a 52 card deck, or even enough for a poker game.

It’s time to get smart – but not too smart. One aim here is not to copy any existing system but develop a new one, and only then compare it with existing systems.

For example, a stacking system that is impervious to “always cut cards” would be if the dealer knows where every card in the uncut deck is before the cut. Then observing the cut will tell the dealer if the result of the cut gives himself a winning or losing hand, and play accordingly. Even if not observing the cut, the first card played will tell the dealer every card in every hand.

But, the dealer doesn’t have to know where every card in the uncut deck is to know if the cut is a winner or loser. So long as the dealer knows which hand at least least one of the cards is in, that gives an edge. Tracking more cards gives more of an edge. or track not a single card each time but a block of cards.

Further, cuts aren’t random. So a stacking could be done to give the dealer an edge for a non-random cut.

Then there’s the stacking process itself. Place certain cards at the back of the deck, then distribute throughout the deck where wanted. For example by one riffle shuffle for a two handed game or a four handed with partners, by two riffle shuffles for a four handed game without partners.

Then for computing, a smarter operation is say we can store results of n shuffles of a big deck. Then we do that twice or three or four times and combine those of the fly. Gets permutations from 2n, 3n or 4n shuffles – exceedingly slow but as fast an algorithm as possible and overcomes the storage problem.

Then there’s the idea of dividing the deck into zones, and working out the fastest way of moving cards from one zone to another. A riffle shuffle moves cards from the centre zone to the end zones, and keeps the end zones relatively intact. For plain shuffles, getting wanted cards out of the middle zone to the end zones is a pain unless the cards are dropped onto the back of the deck. We could mentally cut the deck into 13 zones for example, or 8.

Do we want to give ourselves good cards, our opponent bad cards, or both together? Both together would be more difficult to spot.

How subtle is the stacking process going to be? For instance a collection of plain shuffles dropping cards at the back that ends with one or two riffle shuffles is something of a giveaway that the dealer is stacking cards. How well can stacking be hidden?

mollwollfumble said:

Hmm, 32-bit computers are capable of storing the complete set of permutations of only a 12 card deck, or only the first three shuffles of a 52 card deck. And even then the storage in both cases exceeds a gigabyte.

Neither is sufficient for extrapolation to a full permutation of a 52 card deck, or even enough for a poker game.

It’s time to get smart – but not too smart. One aim here is not to copy any existing system but develop a new one, and only then compare it with existing systems.

For example, a stacking system that is impervious to “always cut cards” would be if the dealer knows where every card in the uncut deck is before the cut. Then observing the cut will tell the dealer if the result of the cut gives himself a winning or losing hand, and play accordingly. Even if not observing the cut, the first card played will tell the dealer every card in every hand.

But, the dealer doesn’t have to know where every card in the uncut deck is to know if the cut is a winner or loser. So long as the dealer knows which hand at least least one of the cards is in, that gives an edge. Tracking more cards gives more of an edge. or track not a single card each time but a block of cards.

Further, cuts aren’t random. So a stacking could be done to give the dealer an edge for a non-random cut.

Then there’s the stacking process itself. Place certain cards at the back of the deck, then distribute throughout the deck where wanted. For example by one riffle shuffle for a two handed game or a four handed with partners, by two riffle shuffles for a four handed game without partners.

Then for computing, a smarter operation is say we can store results of n shuffles of a big deck. Then we do that twice or three or four times and combine those of the fly. Gets permutations from 2n, 3n or 4n shuffles – exceedingly slow but as fast an algorithm as possible and overcomes the storage problem.

Then there’s the idea of dividing the deck into zones, and working out the fastest way of moving cards from one zone to another. A riffle shuffle moves cards from the centre zone to the end zones, and keeps the end zones relatively intact. For plain shuffles, getting wanted cards out of the middle zone to the end zones is a pain unless the cards are dropped onto the back of the deck. We could mentally cut the deck into 13 zones for example, or 8.

Do we want to give ourselves good cards, our opponent bad cards, or both together? Both together would be more difficult to spot.

How subtle is the stacking process going to be? For instance a collection of plain shuffles dropping cards at the back that ends with one or two riffle shuffles is something of a giveaway that the dealer is stacking cards. How well can stacking be hidden?

Am I missing anything?

Yes, way too much.

I’m missing how and when to view the cards. Can the be viewed during the shuffle?
I’m missing whether marking the cards is necessary, useful only as a learning aid, or neither. Bowing cards would help manipulation, notching cards would help identification.
I’m missing how to place cards at the start of the shuffle.
I’m missing how to use multiple simple moves as a replacement for a single complicated move.
I’m missing if there’s a way to use the difference between whether the main image is right way up or upside down.
I’m missing …
…
… a deck of cards. The may not be one in the house.

On the other hand, I have found a deck of cards in the house with the names of classical composers on them. Smaller than standard size. These do have the advantage of the backs of the cards being marked in such a way that I can track by sight the progress of one or more cards through the deck during shuffling while learning.

I’ll try practicing shuffling over the next week or so with a deck of 20 cards … with pictures of classical composers on them.

mollwollfumble said:

I’ll try practicing shuffling over the next week or so with a deck of 20 cards … with pictures of classical composers on them.

Me, shuffling.

mollwollfumble said:

mollwollfumble said:

I’ll try practicing shuffling over the next week or so with a deck of 20 cards … with pictures of classical composers on them.

Me, shuffling.

Hmm, a plain shuffle containing single pair swap, if repeated exactly will cycle back to no change in 4 shuffles. Like Rubik’s cube
Ditto with a single swap of three.
Ditto with any number of non-interacting swaps.
A plain shuffle with two interacting pair swaps, if repeated exactly will cycle back to no change in 6 shuffles.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

I’ll try practicing shuffling over the next week or so with a deck of 20 cards … with pictures of classical composers on them.

Me, shuffling.

Hmm, a plain shuffle containing single pair swap, if repeated exactly will cycle back to no change in 4 shuffles. Like Rubik’s cube
Ditto with a single swap of three.
Ditto with any number of non-interacting swaps.
A plain shuffle with two interacting pair swaps, if repeated exactly will cycle back to no change in 6 shuffles.

Not succeeding in writing an Excel program to shuffle cards.

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Me, shuffling.

Hmm, a plain shuffle containing single pair swap, if repeated exactly will cycle back to no change in 4 shuffles. Like Rubik’s cube
Ditto with a single swap of three.
Ditto with any number of non-interacting swaps.
A plain shuffle with two interacting pair swaps, if repeated exactly will cycle back to no change in 6 shuffles.

Not succeeding in writing an Excel program to shuffle cards.

Now shuffling in Fortran – still a couple of bugs in there.

Enjoying this video – five false card shuffles. Five ways where it looks like a card shuffle but isn’t.

https://www.youtube.com/watch?v=PfbOELSTyP0

mollwollfumble said:

mollwollfumble said:

mollwollfumble said:

Hmm, a plain shuffle containing single pair swap, if repeated exactly will cycle back to no change in 4 shuffles. Like Rubik’s cube
Ditto with a single swap of three.
Ditto with any number of non-interacting swaps.
A plain shuffle with two interacting pair swaps, if repeated exactly will cycle back to no change in 6 shuffles.

Not succeeding in writing an Excel program to shuffle cards.

Now shuffling in Fortran – still a couple of bugs in there.

Enjoying this video – five false card shuffles. Five ways where it looks like a card shuffle but isn’t.

https://www.youtube.com/watch?v=PfbOELSTyP0

HTF can it be easier to code shuffling in Fortran than doing it in Excel?

I’m still learning to shuffle. I learnt first on 6 cards, then 20, now I’m up to shuffling 28 cards. Only overhand shuffling so far, not riffle shuffle yet. A bit of a slow learning process.

It occurred to me to today that sorting in computer programs is similar to stacking a deck. Suppose you already know where all 52 cards are and you want to sort them into desired order – then the computer algorithm “simple sort” uses pair swaps possible when overhand shuffling cards, but wouldn’t be quite the same. Quicksort using a binary tree is more difficult to do in cards.

But the fastest most robust sorting is heapsort – I wonder, I truly wonder, whether heapsort can be done by hand with a pack of cards?
Or whether there’s a variation of heapsort that can be done using simple shuffling?

The Rev Dodgson said:

mollwollfumble said:

mollwollfumble said:

Not succeeding in writing an Excel program to shuffle cards.

Now shuffling in Fortran – still a couple of bugs in there.

Enjoying this video – five false card shuffles. Five ways where it looks like a card shuffle but isn’t.

https://www.youtube.com/watch?v=PfbOELSTyP0

HTF can it be easier to code shuffling in Fortran than doing it in Excel?

I’d like you to answer that.
Here is the first part of the Fortran code. What would this code in Fortran look like in Excel? I tried to do this in Excel and failed.

ncard=52
do nc=1,ncard
ltaken(nc)=.false. ! value has not already been used
end do
do nc=1,ncard ! generate permutation in reduced form
ireduced(nc)=ceiling((ncard+1-nc)*rand()) ! generates in turn a random integer over ncard, ncard-1, ..., 1
end do
do nc=1,ncard ! expand reduced form to full permutation
irandom(nc)=0
do ir=1,ireduced(nc)
irandom(nc)=irandom(nc)+1
5 continue
if(ltaken(irandom(nc))) then
irandom(nc)=irandom(nc)+1
goto 5
end if
end do
ltaken(irandom(nc))=.true.
end do

?

mollwollfumble said:

I’m still learning to shuffle. I learnt first on 6 cards, then 20, now I’m up to shuffling 28 cards. Only overhand shuffling so far, not riffle shuffle yet. A bit of a slow learning process.

It occurred to me to today that sorting in computer programs is similar to stacking a deck. Suppose you already know where all 52 cards are and you want to sort them into desired order – then the computer algorithm “simple sort” uses pair swaps possible when overhand shuffling cards, but wouldn’t be quite the same. Quicksort using a binary tree is more difficult to do in cards.

But the fastest most robust sorting is heapsort – I wonder, I truly wonder, whether heapsort can be done by hand with a pack of cards?
Or whether there’s a variation of heapsort that can be done using simple shuffling?

The Rev Dodgson said:

mollwollfumble said:

Now shuffling in Fortran – still a couple of bugs in there.

Enjoying this video – five false card shuffles. Five ways where it looks like a card shuffle but isn’t.

https://www.youtube.com/watch?v=PfbOELSTyP0

HTF can it be easier to code shuffling in Fortran than doing it in Excel?

I’d like you to answer that.
Here is the first part of the Fortran code. What would this code in Fortran look like in Excel? I tried to do this in Excel and failed.

ncard=52
do nc=1,ncard
ltaken(nc)=.false. ! value has not already been used
end do
do nc=1,ncard ! generate permutation in reduced form
ireduced(nc)=ceiling((ncard+1-nc)*rand()) ! generates in turn a random integer over ncard, ncard-1, ..., 1
end do
do nc=1,ncard ! expand reduced form to full permutation
irandom(nc)=0
do ir=1,ireduced(nc)
irandom(nc)=irandom(nc)+1
5 continue
if(ltaken(irandom(nc))) then
irandom(nc)=irandom(nc)+1
goto 5
end if
end do
ltaken(irandom(nc))=.true.
end do

?

I’m still trying to unshuffle cards by hand, not all that successfully.