It’s said that a mathematician can’t do up zis shoelaces because there are too many different possible ways to do it. I used to have that problem so now wear shoes without laces.

I’m having much the same problem with carpentry.

My arrangement is as follows.

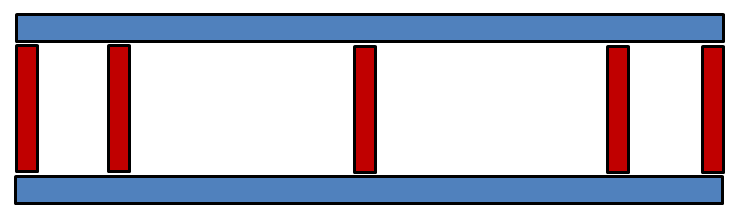
7 pieces of timber, 2 long and 5 short. Because the ends may have slight bevels, or there may be a bit of bowing or twist, the pieces aren’t identical.

It turns out that there are 983040 fundamentally different ways to arrange the seven pieces of timber into this shape. Each of the seven pieces can be flipped side to side or end to end, 4 rotational states, giving 4^7 = 16384 different piece rotations. On top of that there are 5! = 120 different ways to arrange the short pieces and 2 ways to arrange the long pieces. Taking out a factor of 4 for symmetry that gives 4^7 * 120 * 2 / 4 = 983040 fundamentally different ways to make the shape.

As a mathematician, I can’t try all the options to find the best arrangement (minimal gaps where pieces join, minimal overall bend and twist).

As a carpenter?

Perhaps use the longest of the short pieces at the ends with the bevels chosen to match the twists of the long members, then slot the remaining three short pieces in place?

Or longest short piece at one end and shortest short piece at the other, and arrange in order of length then rotate to minimise gaps?

Moll, I recommend watching this video and perhaps a couple similar, of people doing something like what you’re undertaking.

A carpenter would cut fresh pieces all the same length with straight ends :)

pommiejohn said:

A carpenter would cut fresh pieces all the same length with straight ends :)

Have you actually ever met a chippie?

sibeen said:

pommiejohn said:

A carpenter would cut fresh pieces all the same length with straight ends :)

Have you actually ever met a chippie?

Yeah. You can tell a real chippie by the fact that he hasn’t got a full complement of fingers.

Cut the shorter pieces all the same length, use larger screws to hold the longer pieces down onto the shorter pieces firmly, that will get rid of the bends in them.

pommiejohn said:

sibeen said:

pommiejohn said:

A carpenter would cut fresh pieces all the same length with straight ends :)

Have you actually ever met a chippie?

Yeah. You can tell a real chippie by the fact that he hasn’t got a full complement of fingers.

>Looks at fingers<

I think the chipies who are losing fingers these days are more likely to have gambling problems.

;-)

Rule 303 said:

Moll, I recommend watching this video and perhaps a couple similar, of people doing something like what you’re undertaking.

Thanks, will do.

(Dang, lost my great reply to OP). Anyway, the key is to figure out which end of each small piece has the smallest bevel, and call that the bottom. Stand each upright on the straightest long piece (to get the most vertical layout of small pieces) and lay the other long piece along the top and nail down. Then flip over and nail the other long piece on.

Use the most accurately cut of the 5 long pieces as end pieces, nailing them first. Select the longest of the remaining 3 and nail that in the centre. A bit of twiddling to get the bevels to cancel each other out as much as possible. And a bit of brute force in nailing the final long piece and voila – accurate frame give or take a mm or two. Without that strategy it would have had errors of up to 20 mm.

pommiejohn said:

A carpenter would cut fresh pieces all the same length with straight ends :)

Having measured each one twice :)

mollwollfumble said:

Rule 303 said:

Moll, I recommend watching this video and perhaps a couple similar, of people doing something like what you’re undertaking.

Thanks, will do.

(Dang, lost my great reply to OP). Anyway, the key is to figure out which end of each small piece has the smallest bevel, and call that the bottom. Stand each upright on the straightest long piece (to get the most vertical layout of small pieces) and lay the other long piece along the top and nail down. Then flip over and nail the other long piece on.

Use the most accurately cut of the 5 long pieces as end pieces, nailing them first. Select the longest of the remaining 3 and nail that in the centre. A bit of twiddling to get the bevels to cancel each other out as much as possible. And a bit of brute force in nailing the final long piece and voila – accurate frame give or take a mm or two. Without that strategy it would have had errors of up to 20 mm.

The priority here is to make a strong frame that will stay where you put it and hold up the cladding. Don’t worry if it’s a bit rough or ugly, it’s all getting hidden anyway. That said, you will regret it if you don’t get the door right, so pay attention to the minor details there. Keep going mate. :-)