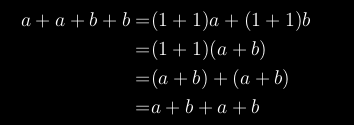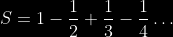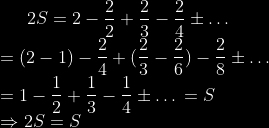Are there any algebras that have non-commutative addition?

It’s fairly easy to show that if an algebra is distributive and has a multiplicative identity then it also has commutative addition:

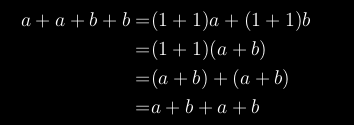
Subtracting the first and last terms on both sides gives

So I suppose the question is equivalent to asking whether there are any algebras that either are not distributive or have no multiplicative identity, although I’m not sure yet whether they’re necessary or sufficient conditions.

well look we don’t know anything much really https://mathworld.wolfram.com/Algebra.html seems to say that An algebra is sometimes implicitly assumed to be associative or to possess a multiplicative identity. so make of that what we will

we haven’t read the whole article

SCIENCE said:

we haven’t read the whole article

Get thee behind me Satan!

Witty Rejoinder said:

SCIENCE said:

we haven’t read the whole article

Get thee behind me Satan!

in front or behind, summarily does it matter

btm said:

Are there any algebras that have non-commutative addition?

It’s fairly easy to show that if an algebra is distributive and has a multiplicative identity then it also has commutative addition:

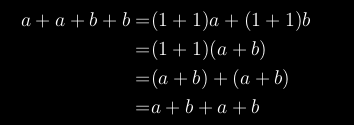
Subtracting the first and last terms on both sides gives

So I suppose the question is equivalent to asking whether there are any algebras that either are not distributive or have no multiplicative identity, although I’m not sure yet whether they’re necessary or sufficient conditions.

Gotta think a bit more about this.

For starters, the use of symbols + and * are arbitrary, unless both are used together in field theory. In group theory (a group is not necessarily a field) is common to omit these symbols altogether and write a + a + b + b as aabb.

There are plenty on non-commutative groups. The question then is whether it is possible to build a field on a non-abelian (ie. non-commutative) group.

I’ve never known the difference between a ‘field’ and a ‘ring’. So I’m going to be cautious and rewrite the above question “is it possible to build a ring on a non-abelian group”. Mr google finds the following entry. https://math.stackexchange.com/questions/833270/rings-with-noncommutative-addition.

That entry links to “near-rings”. https://en.wikipedia.org/wiki/Near-ring so let’s see what Mr wiki has to say.

“In mathematics, a near-ring is an algebraic structure similar to a ring but satisfying fewer axioms. Near-rings arise naturally from functions on groups.”

“Many applications involve the subclass of near-rings known as near-fields”

A near-field is not the same, it only has a right distributive law not a left distributive law, but it requires addition to be commutative, so a near-field doesn’t answer the original question.

c -

A man walks into a bookshop and says “I can’t remember the title but it is about group, field and ring theory”. The shop assistant looks in the sports section. The look on the shop assistant’s face when the book is finally found, titled “topics in algebra”, was priceless.

Thank you btm for a great question.

If it’s not commutative , it’s not addition

dv said:

If it’s not commutative , it’s not addition

¿ref

SCIENCE said:

dv said:

If it’s not commutative , it’s not addition

¿ref

def

dv said:

SCIENCE said:

dv said:

If it’s not commutative , it’s not addition

¿ref

def

Surely it depends what you are adding, and how you add it.

The Rev Dodgson said:

dv said:

SCIENCE said:

¿ref

def

Surely it depends what you are adding, and how you add it.

axioms

Numbers is numbers.

To elaborate the engineers’ perspective on this:

If we pretend that for real materials stress/strain is exactly constant, then we can add loads to a structure in any order, and always end up with the same deflection.

But if we recognise that stress/strain is not constant for any real material, then it often makes a difference which order you apply the loads in.

So addition of loads to non-linear materials is not commutative.

in that sense even the addition of what we usually understand as numbers, on an electronic calculator, is non-commutative

(and one way to resolve that problem is to sort by ascending size before addition)

SCIENCE said:

in that sense even the addition of what we usually understand as numbers, on an electronic calculator, is non-commutative

(and one way to resolve that problem is to sort by ascending size before addition)

Isn’t it?

Can you give a simple example?

The Rev Dodgson said:

SCIENCE said:

in that sense even the addition of what we usually understand as numbers, on an electronic calculator, is non-commutative

(and one way to resolve that problem is to sort by ascending size before addition)

Isn’t it?

Can you give a simple example?

{1e-16 + }_1000000 1 ¿=? 1 {+ 1e-16}_1000000

SCIENCE said:

The Rev Dodgson said:

SCIENCE said:

in that sense even the addition of what we usually understand as numbers, on an electronic calculator, is non-commutative

(and one way to resolve that problem is to sort by ascending size before addition)

Isn’t it?

Can you give a simple example?

{1e-16 + }_1000000 1 ¿=? 1 { + 1e-16}_1000000

sorry, fixed with the correct spacing, we hope

SCIENCE said:

The Rev Dodgson said:

SCIENCE said:

in that sense even the addition of what we usually understand as numbers, on an electronic calculator, is non-commutative

(and one way to resolve that problem is to sort by ascending size before addition)

Isn’t it?

Can you give a simple example?

{1e-16 + }_1000000 1 ¿=? 1 {+ 1e-16}_1000000

Sorry, not sure what all the squiggles mean.

It’s not just addition though, is it?

The Rev Dodgson said:

SCIENCE said:

The Rev Dodgson said:

Isn’t it?

Can you give a simple example?

{1e-16 + }_1000000 1 ¿=? 1 {+ 1e-16}_1000000

Sorry, not sure what all the squiggles mean.

It’s not just addition though, is it?

what does an electronic calculator do then

SCIENCE said:

The Rev Dodgson said:

SCIENCE said:

{1e-16 + }_1000000 1 ¿=? 1 {+ 1e-16}_1000000

Sorry, not sure what all the squiggles mean.

It’s not just addition though, is it?

what does an electronic calculator do then

Subtract, multiply, divide, exponentiate as well?

The Rev Dodgson said:

SCIENCE said:

The Rev Dodgson said:

Sorry, not sure what all the squiggles mean.

It’s not just addition though, is it?

what does an electronic calculator do then

Subtract, multiply, divide, exponentiate as well?

well yes we’re sure some of those operations are also noncommutative on an electronic calculator but just answering for the additive case we were

ok Rev heads up you can try this on your electronic calculator but your precision may vary

s1 = s2 = 0;
s1 += 1;
for (n = 0; n < 1000; n++) {
 s1 += 1e-17;
 s2 += 1e-17;
}
s2 += 1;
alert(s2 - s1);

SCIENCE said:

ok Rev heads up you can try this on your electronic calculator but your precision may vary

s1 = s2 = 0;
s1 += 1;
for (n = 0; n < 1000; n++) {
 s1 += 1e-17;
 s2 += 1e-17;
}
s2 += 1;
alert(s2 - s1);

I’ll just do that in the electronic calculator in my head.

So we can generalise that as if the set of valid numbers is finite then addition is not always commutative.

The Rev Dodgson said:

To elaborate the engineers’ perspective on this:

If we pretend that for real materials stress/strain is exactly constant, then we can add loads to a structure in any order, and always end up with the same deflection.

But if we recognise that stress/strain is not constant for any real material, then it often makes a difference which order you apply the loads in.

So addition of loads to non-linear materials is not commutative.

That’s a really good point.

In brief, if you have a non-commutative operator, call it something other than addition

so what should we call what electronic calculators do

SCIENCE said:

so what should we call what electronic calculators do

Fail

SCIENCE said:

so what should we call what electronic calculators do

And what do we call it when we find the deflections in a structure due to two different load conditions, and combine the values at each point to find the total deflections in the structure?

The Rev Dodgson said:

SCIENCE said:

so what should we call what electronic calculators do

And what do we call it when we find the deflections in a structure due to two different load conditions, and combine the values at each point to find the total deflections in the structure?

What would you like to call it? You’ve already successfully proven it’s not additive.

The Rev Dodgson said:

SCIENCE said:

so what should we call what electronic calculators do

And what do we call it when we find the deflections in a structure due to two different load conditions, and combine the values at each point to find the total deflections in the structure?

You could say that you’re doing calculations involving factors other than addition.

dv said:

The Rev Dodgson said:

SCIENCE said:

so what should we call what electronic calculators do

And what do we call it when we find the deflections in a structure due to two different load conditions, and combine the values at each point to find the total deflections in the structure?

What would you like to call it? You’ve already successfully proven it’s not additive.

If you combine the numbers in the right sequence, you can use addition, so I’d call it addition.

Also, that’s what other people call it.

we’re not prescriptivists but we think we’re with The Rev Dodgson on this one

dv said:

SCIENCE said:

so what should we call what electronic calculators do

Fail

Also fair, though also unfair.

dv said:

If it’s not commutative , it’s not addition

So you’re defining addition as commutative? Or are you assuming that all algebras are Abelian?

btm said:

dv said:

If it’s not commutative , it’s not addition

So you’re defining addition as commutative? Or are you assuming that all algebras are Abelian?

I’m saying that the term “addition” is only extended to non-numbers by choice, and there is no value in choosing to extend that term to cover operations that don’t share addition’s core properties, among which is commutation.

lol

what a jolly fellow

once upon a time ghleyhm was a word

SCIENCE said:

once upon a time ghleyhm was a word

But not one you’d expect to encounter in a journal.

The series

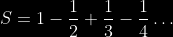
is known to converge (to ln(2)). Multiplying both sides by 2 gives

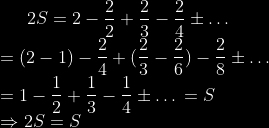
This fails because the initial series, while convergent, is not absolutely convergent, and rearranging the terms of a series that’s not absolutely convergent gives inconsistent (or, as in this case, nonsense) results.

This seems to me to qualify as an example of non-commutative addition.

btm said:

The series

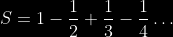
is known to converge (to ln(2)). Multiplying both sides by 2 gives

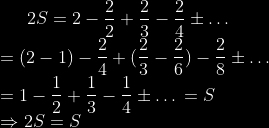
This fails because the initial series, while convergent, is not absolutely convergent, and rearranging the terms of a series that’s not absolutely convergent gives inconsistent (or, as in this case, nonsense) results.

This seems to me to qualify as an example of non-commutative addition.

No. That’s more about the properties of limits and infinity than the properties of addition. Note that rearranging a finite number of terms does not alter the sum.