Final dance of unequal black hole partners

Solving the equations of general relativity for colliding black holes is no simple matter.

more…

Tau.Neutrino said:

Final dance of unequal black hole partners

Solving the equations of general relativity for colliding black holes is no simple matter.

more…

See also https://tokyo3.org/forums/holiday/topics/14368/

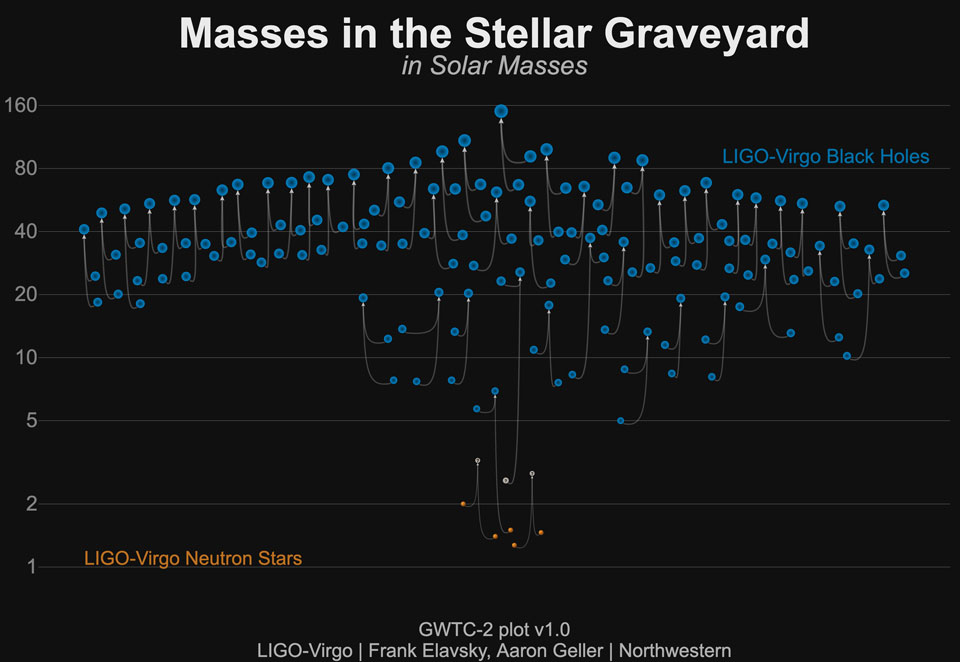
> Modeling pairs of black holes with very different masses is very computational demanding because of the need to maintain accuracy in a wide range of grid resolutions

I don’t get it. It’s just two points moving in orbit until the black holes are nearly on top of each other. And after that you still need only one grid resolution – that of the BH horizon. Don’t even need to solve the conservation of energy/momentum equation.

Why difficult? Oh, I see, the actual coalescence of singularities requires two grid resolutions. But only the fine resolution affects the trajectories in that split second, the rest can be post-calculated at coarse resolution from the pre-calculated trajectories.

> Like computer models in many fields, Lousto uses a method called adaptive mesh refinement

I’ve used that in fluid dynamics. No biggie. But not necessarily the best solution here. A Lagrange-Eulerian method would be better. Lagrange for the trajectories and Eulerian for the event horizons and gravitational waves.

> The simulation isn’t the end of the road. Black holes can have a variety of spins and configurations, which impact the amplitude and frequency of the gravitational waves their merger produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “templates” to compare with future detections.

Agree with that one. Spins, eccentricities and inclinations.

> By halving and halving the mass ratio while adding internal grid refinement levels, they were able to go from 32:1 black hole mass ratios to 128:1 binary systems that undergo 13 orbits before merger.

That’s pretty standard.

> On Frontera supercomputer, it required seven months of constant computation. Frontera was the perfect tool for the job. Our problem requires high performance processors, communication, and memory, and Frontera has all three.

I bet I could do it on a standard PC. Without adaptive meshes.

mollwollfumble said:

Tau.Neutrino said:

Final dance of unequal black hole partners

Solving the equations of general relativity for colliding black holes is no simple matter.

more…

See also https://tokyo3.org/forums/holiday/topics/14368/

> Modeling pairs of black holes with very different masses is very computational demanding because of the need to maintain accuracy in a wide range of grid resolutions

I don’t get it. It’s just two points moving in orbit until the black holes are nearly on top of each other. And after that you still need only one grid resolution – that of the BH horizon. Don’t even need to solve the conservation of energy/momentum equation.

Why difficult? Oh, I see, the actual coalescence of singularities requires two grid resolutions. But only the fine resolution affects the trajectories in that split second, the rest can be post-calculated at coarse resolution from the pre-calculated trajectories.

> Like computer models in many fields, Lousto uses a method called adaptive mesh refinement

I’ve used that in fluid dynamics. No biggie. But not necessarily the best solution here. A Lagrange-Eulerian method would be better. Lagrange for the trajectories and Eulerian for the event horizons and gravitational waves.

> The simulation isn’t the end of the road. Black holes can have a variety of spins and configurations, which impact the amplitude and frequency of the gravitational waves their merger produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “templates” to compare with future detections.

Agree with that one. Spins, eccentricities and inclinations.

> By halving and halving the mass ratio while adding internal grid refinement levels, they were able to go from 32:1 black hole mass ratios to 128:1 binary systems that undergo 13 orbits before merger.

That’s pretty standard.

> On Frontera supercomputer, it required seven months of constant computation. Frontera was the perfect tool for the job. Our problem requires high performance processors, communication, and memory, and Frontera has all three.

I bet I could do it on a standard PC. Without adaptive meshes.

Hold on, Perhaps I’m wrong. (Or perhaps not).

Space tells matter how to move.
Matter tells space how to curve.

If I have to integrate out that curvature then they’re right, you do need … no, even then, a single Eulerian grid scale will suffice.

And if there is no gravitational self-interaction (ie. assuming the gravitational field of a singularity cannot affect the motion of that singularity) then the gravitational field from a single body suffices to determine the motion of the other body, and the problem reduces to Lagrangian-Langrangian calculation, which could even be done on an Excel spreadsheet.

This applies even if, as seems likely, there are non-linear interactions between the gravitational fields. In this case the non-linear interactions would affect the gravitational wave, a bit, but not the trajectories.

The equations of GR are expressed in Eulerian terms, so they would need to be rewritten in Lagrangian terms before solution. A shortcut would be to take the timestep to be the distance between the bodies, times the speed of light, times a small integer (1, 2 or 3).

Using a method I adapted from an astrophysicist, the acceleration would be stepwise linear, making the velocity stepwise quadratic and the position a cubic spline. I found this gave great accuracy and speeded up that astrophysicist’s calculations by a huge factor.

Could it already be that they’re using a Lagrangian-Eurlerian formulation? That’s suggested by their ability to swap masses, change a 1:32 mass ratio to a 1:128 mass ratio with the flick of a switch.

In which case the high computer usage would be in order to get pretty pictures, rather than any effect it would have on the gravitational wave strength received on Earth.

I suppose I need to look up the original paper.

mollwollfumble said:

mollwollfumble said:

Tau.Neutrino said:

Final dance of unequal black hole partners

Solving the equations of general relativity for colliding black holes is no simple matter.

more…

See also https://tokyo3.org/forums/holiday/topics/14368/

> Modeling pairs of black holes with very different masses is very computational demanding because of the need to maintain accuracy in a wide range of grid resolutions

I don’t get it. It’s just two points moving in orbit until the black holes are nearly on top of each other. And after that you still need only one grid resolution – that of the BH horizon. Don’t even need to solve the conservation of energy/momentum equation.

Why difficult? Oh, I see, the actual coalescence of singularities requires two grid resolutions. But only the fine resolution affects the trajectories in that split second, the rest can be post-calculated at coarse resolution from the pre-calculated trajectories.

> Like computer models in many fields, Lousto uses a method called adaptive mesh refinement

I’ve used that in fluid dynamics. No biggie. But not necessarily the best solution here. A Lagrange-Eulerian method would be better. Lagrange for the trajectories and Eulerian for the event horizons and gravitational waves.

> The simulation isn’t the end of the road. Black holes can have a variety of spins and configurations, which impact the amplitude and frequency of the gravitational waves their merger produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “templates” to compare with future detections.

Agree with that one. Spins, eccentricities and inclinations.

> By halving and halving the mass ratio while adding internal grid refinement levels, they were able to go from 32:1 black hole mass ratios to 128:1 binary systems that undergo 13 orbits before merger.

That’s pretty standard.

> On Frontera supercomputer, it required seven months of constant computation. Frontera was the perfect tool for the job. Our problem requires high performance processors, communication, and memory, and Frontera has all three.

I bet I could do it on a standard PC. Without adaptive meshes.

Hold on, Perhaps I’m wrong. (Or perhaps not).

Space tells matter how to move.
Matter tells space how to curve.

If I have to integrate out that curvature then they’re right, you do need … no, even then, a single Eulerian grid scale will suffice.

And if there is no gravitational self-interaction (ie. assuming the gravitational field of a singularity cannot affect the motion of that singularity) then the gravitational field from a single body suffices to determine the motion of the other body, and the problem reduces to Lagrangian-Langrangian calculation, which could even be done on an Excel spreadsheet.

This applies even if, as seems likely, there are non-linear interactions between the gravitational fields. In this case the non-linear interactions would affect the gravitational wave, a bit, but not the trajectories.

The equations of GR are expressed in Eulerian terms, so they would need to be rewritten in Lagrangian terms before solution. A shortcut would be to take the timestep to be the distance between the bodies, times the speed of light, times a small integer (1, 2 or 3).

Using a method I adapted from an astrophysicist, the acceleration would be stepwise linear, making the velocity stepwise quadratic and the position a cubic spline. I found this gave great accuracy and speeded up that astrophysicist’s calculations by a huge factor.

Could it already be that they’re using a Lagrangian-Eurlerian formulation? That’s suggested by their ability to swap masses, change a 1:32 mass ratio to a 1:128 mass ratio with the flick of a switch.

In which case the high computer usage would be in order to get pretty pictures, rather than any effect it would have on the gravitational wave strength received on Earth.

I suppose I need to look up the original paper.

>> The simulation isn’t the end of the road. Black holes can have a variety of spins and configurations, which impact the amplitude and frequency of the gravitational waves their merger produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “templates” to compare with future detections.

> Agree with that one. Spins, eccentricities and inclinations.

More than 12 times in all, wouldn’t it? Perhaps not. Because ze is using an Eulerian framework, all possible directions to Earth are covered in a single simulation.

That means you can eliminate inclination of the orbital plane, and stick to inclination of the two spins relative to the orbital plane. Varying that and initial eccentricity could be done in about 12 simulations per mass ratio. As you were.