The internet has the answer [spoiler] but just for entertainment here you go.
The internet has the answer [spoiler] but just for entertainment here you go.

SCIENCE said:
The internet has the answer [spoiler] but just for entertainment here you go.
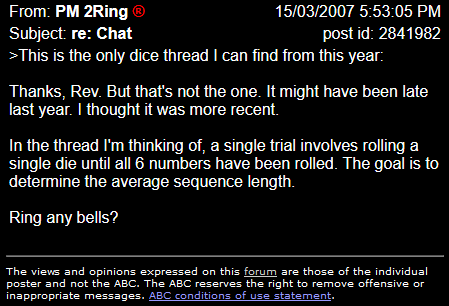
This from the chat thread, or what?
Chat thread in 2007, so over on the old forum I’m assuming.
sibeen said:
Chat thread in 2007, so over on the old forum I’m assuming.
Well as I said in the other thread, my time machine’s not working at the moment.
SCIENCE said:
The internet has the answer [spoiler] but just for entertainment here you go.
Doesn’t ring bells. But let’s start with a coin.
Probability, Length
1/2, 2
1/4, 3
1/8, 4
So for coins it has a finite answer:
2/2^1 + 3/2^2 + 4/2^3 + …
For dice it would also have a finite answer, not too difficult to calculate.
mollwollfumble said:
not too difficult to calculate.
You’re right, there, explained it that time too.

SCIENCE said:
mollwollfumble said:
not too difficult to calculate.
You’re right, there, explained it that time too.
I worked that out whilst walking the dog this afternoon.
Only 14 years late.
Well those were the days, and it was a good question, we use it on our students now too.
| From: poisson du jour ® | 2/08/2006 11:46:09 AM |
| Subject: trivia Q | post id: 2443261 |
| Question at trivs last night. On average, how many times would you have to throw a dice for every number to come up? | |
| From: SqueezeBabe ® | 2/08/2006 11:47:01 AM |
| Subject: re: trivia Q | post id: 2443263 |
| perfect world = 6 shrugs apart from that i don’t know… | |
| From: Deity of the Day ® | 2/08/2006 11:47:42 AM |
| Subject: re: trivia Q | post id: 2443265 |
| On average, how many times would you have to throw a dice for every number to come up? ]] Another good trivia question: how long is a peice of string? | |
| From: Angus Prune ® | 2/08/2006 11:47:52 AM |
| Subject: re: trivia Q | post id: 2443266 |
| 6 would be the minimum. The average would have to be higher than that. | |
| From: Supercollider ® | 2/08/2006 11:47:58 AM |
| Subject: re: trivia Q | post id: 2443267 |
| You might go on throwing it forever without all the numbers coming up, but this isn’t likely. | |
| From: Supercollider ® | 2/08/2006 11:49:20 AM |
| Subject: re: trivia Q | post id: 2443271 |
| Oops, I ignored the ‘on average’ bit. | |
| From: poisson du jour ® | 2/08/2006 11:49:59 AM |
| Subject: re: trivia Q | post id: 2443273 |
| The question says, on average. So if you had an infinite number of trials, what would be the average number of throws before all 6 sides came up? | |
| From: SqueezeBabe ® | 2/08/2006 11:51:14 AM |
| Subject: re: trivia Q | post id: 2443274 |
| So if you had an infinite number of trials<< then you can’t have an average, technically speaking… | |
| From: PeterT1 ® | 2/08/2006 11:55:36 AM |
| Subject: re: trivia Q | post id: 2443283 |
| It’s a permutation and combination question, do they still do that at school? | |
| From: Purple ® | 2/08/2006 11:57:51 AM |
| Subject: re: trivia Q | post id: 2443293 |
| isn’t it 1/6 × 1/6 × 1/6 etc? though that doesn’t look right at all | |
| From: home_quays ® | 2/08/2006 12:19:24 PM |
| Subject: re: trivia Q | post id: 2443344 |
| If we re-phrased the question and asked alot of questions for a specific outcome then we could chart probability v’s no. of throws etc. probability relates to a specific event. The question as stated is pretty open ended. (like how long is a piece of string) IMO | |
| From: IDAK ® | 2/08/2006 12:24:19 PM |
| Subject: re: trivia Q | post id: 2443352 |
| Are you going to give Trivia comp’s answer? | |
| From: memeist ® | 2/08/2006 12:29:33 PM |
| Subject: re: trivia Q | post id: 2443361 |
| For a 6-sided die, 6×6=36 times; on the odds, each number will come up at least once almost every time. A mathematician may have a better answer, though. | |
| From: skye ® | 2/08/2006 12:29:43 PM |
| Subject: re: trivia Q | post id: 2443362 |
| >>Are you going to give Trivia comp’s answer? I think the stated answer was 14.3, or 14 to the nearest whole number. No idea how it was derived. We guessed 36, being an average of 6 throws for each face. | |
| From: Topher ® | 2/08/2006 12:35:04 PM |
| Subject: re: trivia Q | post id: 2443373 |
| There’s a distribution that’s suited to these kind of questions- maybe a poisson distirbution. There are ways to work it out mathematically, but I can’t remember what they are. | |
| From: poisson du jour ® | 2/08/2006 12:36:31 PM |
| Subject: re: trivia Q | post id: 2443378 |
| >>I think the stated answer was 14.3, or 14 to the nearest whole number I thought it was 16. Anyway, we were nowhere near. | |
| From: Angus Prune ® | 2/08/2006 12:52:18 PM |
| Subject: re: trivia Q | post id: 2443410 |
| Could someone work up a simulation, get the answer by the brute force method? | |
| From: Topher ® | 2/08/2006 1:11:54 PM |
| Subject: re: trivia Q | post id: 2443450 |
| I’ve done anout 60 simualtions on a spreadsheet, and got an average of 16, with 95% CIs of +/- 1.6. 14 does seem a little low. | |
| From: furu tanuki ® | 2/08/2006 1:50:47 PM |
| Subject: re: trivia Q | post id: 2443565 |
| I calculate 14.7 exactly. | |
| From: furu tanuki ® | 2/08/2006 1:53:23 PM |
| Subject: re: trivia Q | post id: 2443572 |
| With the roll most likely to get the last number being the 11th. | |
| From: mollwollfumble (Physics) | 2/08/2006 2:16:31 PM |
| Subject: re: trivia Q | post id: 2443635 |
| > I calculate 14.7 exactly. Is that mean or median? | |
| From: furu tanuki ® | 2/08/2006 2:35:22 PM |
| Subject: re: trivia Q | post id: 2443692 |
| mean | |
| From: dilly sick ® | 2/08/2006 3:38:15 PM |
| Subject: re: trivia Q | post id: 2443814 |
| yeah i’d say somewhere between 6 and infinity | |
| From: skye ® | 2/08/2006 3:56:33 PM |
| Subject: re: trivia Q | post id: 2443865 |
How did you do it, furu? | |
| From: Martin B ® | 2/08/2006 3:58:55 PM |
| Subject: re: trivia Q | post id: 2443869 |
| “On average, how many times would you have to throw a dice for every number to come up?” Since I am not in a position to add anything to the maths I’ll point out that you an have “dice” or “a die” but not “a dice” : | |
| From: ratwan2 ® | 2/08/2006 3:59:41 PM |
| Subject: re: trivia Q | post id: 2443870 |
| true | |
| From: furu tanuki ® | 2/08/2006 5:25:49 PM |
| Subject: re: trivia Q | post id: 2444073 |
| >>>>> How did you do it, furu? <<<<< P(n,r) = probability of having seen n different numbers after r rolls. P(1,1) = 1, P(2,1) = P(3,1) = P(4,1) = P(5,1) = P(6,1) = 0 For n=1,..,6 and r > 1 P(n,r) = (1-(n-1)/6)*P(n-1,r-1) + (n/6)*P(n,r-1) Put that into Excel up to r = 500 Sum(r*(P(6,r) P(6,r-1))) = 14.7 | |
| From: poisson du jour ® | 2/08/2006 7:06:08 PM |
| Subject: re: trivia Q | post id: 2444135 |
Nil comprende. (Clever bugger.) | |
| From: The Rev Dodgson (Eng Sci) | 2/08/2006 7:08:16 PM |
| Subject: re: trivia Q | post id: 2444136 |
| >> Put that into Excel up to r = 500 << … or any other spreadsheet you happen to have available :) | |
| From: mollwollfumble (Physics) | 3/08/2006 8:59:56 AM |
| Subject: re: trivia Q | post id: 2444929 |
| > I calculate 14.7 exactly. Last night I saw why, and you don’t need Excel to do it. If the probability of an event on one throw is n/6 then the expected number of throws to get that event is 6/n. So the expected number of throws E to get all 6 numbers on a die (singular of dice) is: E = 6/6 + 6/5 + 6/4 + 6/3 + 6/2 + 6/1 = 12 + 1.5 + 1.2 = 14.7. “I may be slow but I get there in the end”. | |
| From: furu tanuki ® | 3/08/2006 10:36:15 AM |
| Subject: re: trivia Q | post id: 2445050 |
| Ah, a true gentleman never resorts to a spreadsheet. Of course the fact that the number of throws to the next novel number is independent of the number of throws to achieve the previous novel number, and therefore the expectation of the sum is equal to the sum of the expectations, goes without saying. | |
| From: The Rev Dodgson (Eng Sci) | 3/08/2006 10:41:17 AM |
| Subject: re: trivia Q | post id: 2445056 |
| >> Last night I saw why, and you don’t need Excel to do it. << If we must refer to spreadsheets as excel, can we at least use a small e? :) >> If the probability of an event on one throw is n/6 then the expected number of throws to get that event is 6/n. So the expected number of throws E to get all 6 numbers on a die (singular of dice) is: E = 6/6 + 6/5 + 6/4 + 6/3 + 6/2 + 6/1 = 12 + 1.5 + 1.2 = 14.7. << Nice, I can follow that. >> “I may be slow but I get there in the end”. << Some of us are slower still :) | |
Thanks for that.
Looks like I was still using 123 as my spreadsheet of choice back then :)
but does Newton 123 Bach have quite the same ring to it
SCIENCE said:
but does Newton 123 Bach have quite the same ring to it
:)
Not sure what happened between 2006 and 2008 to make me finally realise that 123 was really a dead duck.
That was fascintinatingering..
I forgot The Rev used to wear that red shirt.
Seeing as it’s a holiday, VBA code to count the number of rolls required to get all 6 numbers:
Function CountRolls(Iterations As Long)
Dim CountA() As Long, nRolls As Long, totRolls As Long, i As Long, j As Long, nMatch As Long, Maxrolls As Long, MinRolls As Long, Roll As Long
Dim ResA(1 To 3) As Double
Maxrolls = 6
MinRolls = 1000
For i = 1 To Iterations
ReDim CountA(1 To 6)
nMatch = 0
nRolls = 0
Do While nMatch < 6
nRolls = nRolls + 1
Roll = WorksheetFunction.RandBetween(1, 6)
CountA(Roll) = CountA(Roll) + 1
If CountA(Roll) = 1 Then nMatch = nMatch + 1
Loop
totRolls = totRolls + nRolls
If nRolls > Maxrolls Then Maxrolls = nRolls
If nRolls < MinRolls Then MinRolls = nRolls
Next i
ResA(1) = totRolls / Iterations
ResA(2) = Maxrolls
ResA(3) = MinRolls
CountRolls = ResA
End Function
Typical results with Iterations = 100,000:
14.71777, 85, 6
14.70904, 84, 6
Also:
The average number of attempts required to get all 6 numbers in 6 rolls is:
(6^6)/6! = 64.8
since we’re on a roll (and yes we’ll throw our short piece of code in as well) and since that other US Election Tread inspired us to look more closely
we may have been incorrect in claiming that All Was Lost In The Exodus and so we ask
is this The Original ¿ because we will happily load up the rest of it for you all if indeed
SCIENCE said:
since we’re on a roll (and yes we’ll throw our short piece of code in as well) and since that other US Election Tread inspired us to look more closelywe may have been incorrect in claiming that All Was Lost In The Exodus and so we ask
is this The Original ¿ because we will happily load up the rest of it for you all if indeed
That was before my time, but others may recall the historic moment.
SCIENCE said:
yes we’ll throw our short piece of code in as well
rounds = rolls = 0;
o = document.createElement("div");
document.body.appendChild(o);
(roll = function () {
var boost;
var n;
var t;
for (boost = 0; boost < 38421; boost++) {
for (n = 0; n < 6; n++) {
up[n] = 0;
}
for (n = 0; n < 6; ) {
t = Math.floor(Math.random() * 6);
if (up[t] == 0) {
up[t] = 1;
n++;
}
rolls++;
}
rounds++;
}
o.innerHTML = rolls.toString(10) + " rolls in " + rounds.toString(10) + " rounds for an average of " + (rolls / rounds).toString(10) + " rolls per round";
window.requestAnimationFrame(roll);
})();