I’ve got a philosophical issue with fractional calculus. The usually-cited derivation uses the Cauchy integral theorem, but proof of that theorem uses induction, which only applies to integers and can’t be used for rational or real numbers. Other proofs I’ve seen for fractional calculus assume the Cauchy theorem applies and proceed from there. Another approach is to take the Laplace or Fourier transform of the derivative in question; this suffers from the same problem as here: the proofs use induction, but that only applies to integers.
An alternative construction involves repeating the standard definition of the derivative, but delaying taking the limit:
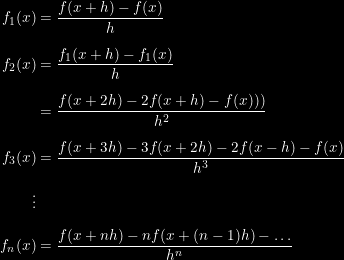
then any rational, irrational, real, or even complex number can be used as n, and the limits applied. Alternatively, if h is very small (as is typical,) this last result can be taken to be a discrete approximation to the nth (n non-integer) derivative.
The problem with this approach is that delaying taking the limit until convenient gives the wrong answer; try finding the 5th derivative of  , for example, using this formula.
, for example, using this formula.
Having said all that, I’ve found application in PID controllers (which I’ve used in solar power charge controllers) and audio controllers.
If you’re interested, have a look at http://cronetoolbox.ims-bordeaux.fr/ for a Matlab (and octave compatible) toolbox for using fractional calculus. The authors presented a paper at an IEEE conference; that paper’s available at sci-hub. Once again, their proofs involve Cauchy’s theorem.
If you really want to learn about fractional calculus, see if you can find the books An introduction to the fractional calculus and fractional differential equations, Miller K.S., Ross B., and The Fractional Calculus Theory And Applications Of Differentiation And Integration To Arbitrary Order, Oldham K B , Spanier J. I’ve got soft copies of these books (both djvu) and can forward them to you if you want them.
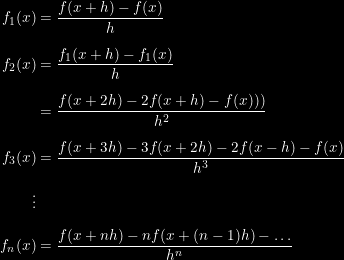
 , for example, using this formula.
, for example, using this formula.