Reading Doc Smith again. Something I thought was obviously ridiculous may not be so ridiculous after all.

In “N-space”, mass and length are as normal but time is intrinsically variable.

By that he means that time is close to constant on planets but highly variable in vacuum.

We all know about time-space rotations caused by gravity in general relativity, but that’s not what he’s talking about. I think I now see what his inspiration is.

If I replace time ‘t’ with temperature ‘T’.

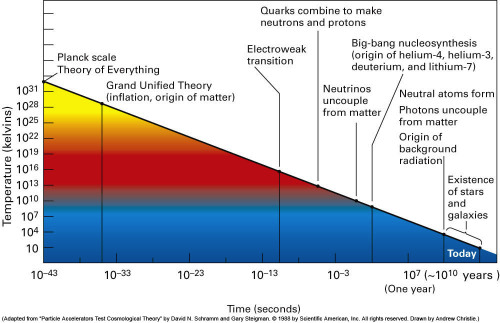
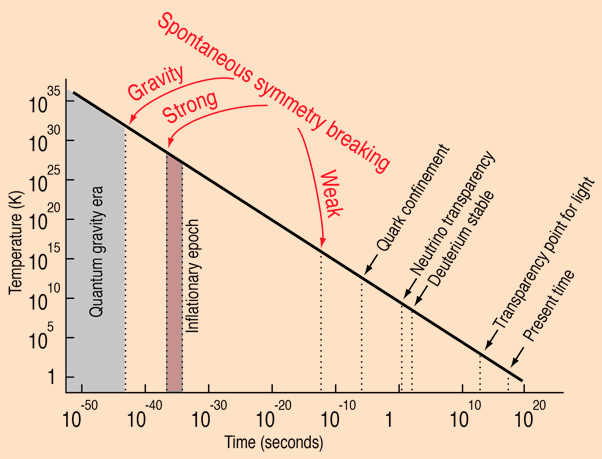
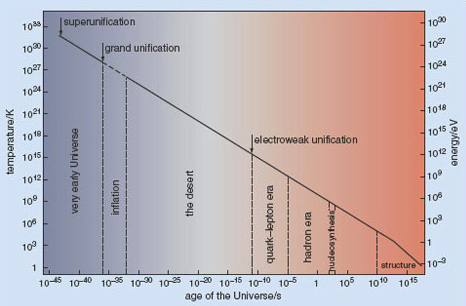
T is nearly constant close to planets (because of conduction and convection), but highly variable in a vacuum. The temperature of space can vary from a couple of degrees Kelvin (CMB) to a couple of million degrees Kelvin (corona), even at the same time. Depending on how T is measured.

Although we think of time as fundamental and temperature as a derived ensemble average, it wasn’t always like that. At the start of the universe, the universe had a well-defined temperature before the universe contained any subatomic particles. So using ensemble averaging as a definition of temperature fails. The arrow of time is defined by entropy, which relates to temperature.

We’re used to symmetry breaking, where for example the weak and electromagnetic forces used to be the single electroweak force at high temperatures. They split as the universe cooled.

But even earlier in the universe, before there were any subatomic particles, inverse temperature and time can be considered to be a single physical variable, that split as the universe cooled. Symmetry breaking.

So the N-space of Doc Smith makes sense if the symmetry breaking of time and temperature resulted in inverse temperature being the universal physical constant instead of time. There could even be a 50% chance of this happening in the early universe. Resulting in some bubbles of cosmic inflation where time is fundamental and others where temperature not time is fundamental.

The constant speed of light would then be defined as distance times temperature rather than distance divided by time, and a slightly modified version of general relativity would still apply.

What do you think?

PS, this is the sort of question I was asking when I was a teenager.

Do we see this happening anywhere?

Spiny Norman said:

Do we see this happening anywhere?

Other than Trans’ head?

mollwollfumble said:

…
Although we think of time as fundamental and temperature as a derived ensemble average, it wasn’t always like that. At the start of the universe, the universe had a well-defined temperature before the universe contained any subatomic particles. So using ensemble averaging as a definition of temperature fails. The arrow of time is defined by entropy, which relates to temperature.

We’re used to symmetry breaking, where for example the weak and electromagnetic forces used to be the single electroweak force at high temperatures. They split as the universe cooled.

But even earlier in the universe, before there were any subatomic particles, inverse temperature and time can be considered to be a single physical variable, that split as the universe cooled. Symmetry breaking.

Dang, I copied a figure illustrating the one-to-one relationship between time and inverse temperature in the earliest universe, where did I put it? There are several of these, let’s post them all here at the bottom of this post.

Now I’ve followed on from this. What if:

a) Time and temperature decoupled at some time in the early universe. Before then, time was just a way of measuring temperature. When would that be?

b) General Relativity and Quantum Mechanics decoupled some time in the early universe? The incompatibility is simply the result of symmetry breaking, nothing more. An essential for that to be true is that the quantum vacuum must form an integral part of general relativity.

c) (Almost) all fine tuning in the universe is the result of symmetry breaking? For example, we know already that the startling similarity between the number of photons and neutrinos in the universe is the result of electroweak symmetry breaking. What if (almost) all the other fine tuning came from symmetry breaking.

d) Dark energy is part of GR and Baryonic matter is part of QM. If we take the fine tuning of dark energy, baryonic matter and dark matter as the result of symmetry breaking then where does that leave Dark Matter? Could it be that DM doesn’t follow the rules of either GR ot QM? In which case dark matter is not supersymmetry (because that’s part of QM) or modified gravity (because that’s part of GR) but something else. Could one possibility for that something else interact gravitons? If so, then it would be testable. Because gravity interacting by gravitons doesn’t follow GR. If I remember correctly, the bending of light by gravitons differs from that of GR, so a test would be to look for a difference between dark matter calculated from galaxy cluster kinematics and dark matter calculated from gravitational lensing.