I don’t know how to start this thread. Perhaps with a history.
I noted while doing a jigsaw puzzle on tablet that the eye is exceptionally good at discerning changes of visual texture, as good as it is at discerning changes in colour.
Which led me to wonder how a texture can be expressed mathematically. Could there be a mathematical way to classify all 2-D textures?
Textures tend to be classified now by what natural item has those textures – wood or paint, fur, feathers, pebbles, skin, sand, cloud, fabrics, random, brick etc., but I want to move beyond that.
Here are some images of computer-generated 3-D spiny and scaly textures.


There are ways to generate textures using random numbers (eg. white, red and blue noise) with control over parameters such as blur, anisotropy, alignment.
There are ways to interpolate texture mapping between key frames in a movie, if the changes aren’t too radical.
There are ways to map texture onto triangles, and onto a type of aperiodic tiling called Wang tiles. Here are some images of Wang tiles.
But the way that seems to offer the greatest hope of mathematically classifying 2-D textures seems to come from the world of using cognitive neural networks to create textures that simulate pre-existing texture images. https://arxiv.org/pdf/1606.01286.pdf and https://arxiv.org/pdf/1505.07376.pdf and “. Portilla and E. P. Simoncelli. A Parametric Texture Model Based on Joint Statistics of Complex Wavelet Coefficients. International Journal of Computer Vision, 40(1):49–70, October 2000”.
This seems to work using the https://en.wikipedia.org/wiki/Gram_matrix which is a bit technical. Wikipedia defines it as “In linear algebra, the Gram matrix of a set of vectors v1 to vn in an inner product space is the Hermitian matrix of inner products, whose entries are given by the inner product Gij.” and “For finite-dimensional real vectors in R^n with the usual Euclidean dot product, the Gram matrix is G = V^T V.” OK, not too technical.
Original texture left and new texture from neural network (with six layers) right.
Original texture left and new texture from neural network (with six layers) right.
Original texture left and new texture from neural network (with six layers) right.




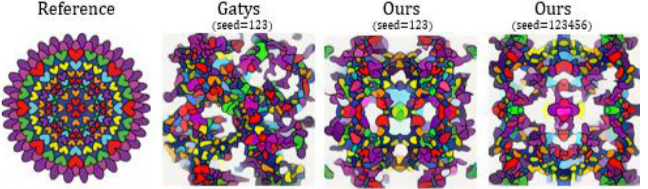
Patterns with symmetric features don’t always work so well. Three cases of symmetry.
What seems to break the algorithm here is that the pattern is too big to handle. The software isn’t designed to handle coherence over such large distances, as with Leonardo Dicaprio’s face. And it shouldn’t be designed for such large distances, because then it is no longer a “texture” but instead a “pattern”.