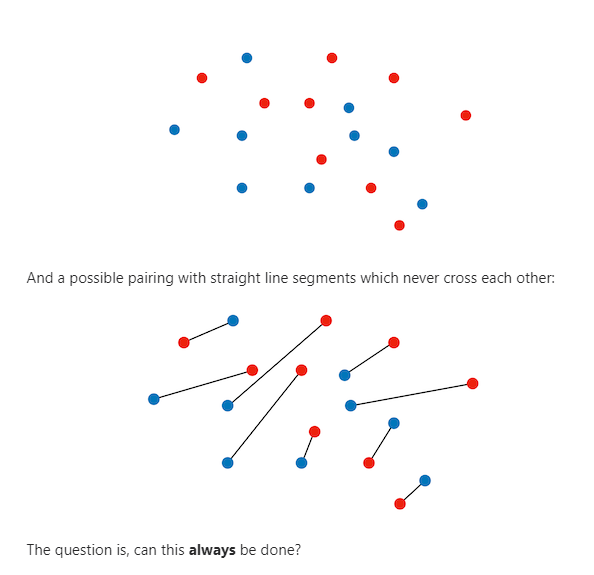
OK, don’t say you weren’t warned.
For any collection of connected points, there will be at least one that has the minimum total length of all the segments. There may be more than one, but there must be just one minimum length.
If the points are connected so that the total length is a minimum, then we can be sure that there are no intersecting lines.
How can we be sure of that?
Because if any two lines do intersect the four points can be reconnected so that they don’t intersect, and it can be shown with simple geometry that the non-intersecting lines have a shorter total length than the intersecting lines.
So if the collection of connected points has any intersecting lines, that collection does not have the shortest total length.
So the shortest total length collection does not have any intersections.