Let’s take a break from crocodilian calculus with a relaxing basic algebra problem.

Find x

27 ^x – 12 ^x = 8 ^x + 12 ^x

dv said:

Let’s take a break from crocodilian calculus with a relaxing basic algebra problem.

Find x

27 ^x – 12 ^x = 8 ^x + 12 ^x

that doesn;t look like it will be a very elegant solution

diddly-squat said:

dv said:

Let’s take a break from crocodilian calculus with a relaxing basic algebra problem.

Find x

27 ^x – 12 ^x = 8 ^x + 12 ^x

that doesn;t look like it will be a very elegant solution

yuck.. what made you choose that?

x = 1.1868……..

diddly-squat said:

diddly-squat said:

dv said:

Let’s take a break from crocodilian calculus with a relaxing basic algebra problem.

Find x

27 ^x – 12 ^x = 8 ^x + 12 ^x

that doesn;t look like it will be a very elegant solution

yuck.. what made you choose that?

x = 1.1868……..

Show working.

What is this “math”?

buffy said:

What is this “math”?

I’m just following on from fsm

dv said:

buffy said:

What is this “math”?

I’m just following on from fsm

I didn’t approve then either…

buffy said:

dv said:

buffy said:

What is this “math”?

I’m just following on from fsm

I didn’t approve then either…

Well I applaud your consistency.

Ah well hopefully Rev will have a go at it

It’s the math vs maths that is irking Buffy.

Witty Rejoinder said:

It’s the math vs maths that is irking Buffy.

Yes.

Witty Rejoinder said:

It’s the math vs maths that is irking Buffy.

Of course. It is either math. (with the full stop to indicate you have shortened it). Or it is “maths” (which is a contraction and doesn’t need the full stop). And Mr. is also wrong and irksome. It doesn’t need that full stop.

Witty Rejoinder said:

It’s the math vs maths that is irking Buffy.

Me too.

I wonder why it’s called “mathematics” rather than mathematry.

We don’t call geometry “geometrics”.

Bubblecar said:

I wonder why it’s called “mathematics” rather than mathematry.

We don’t call geometry “geometrics”.

Yes but you usually draw geometry and mathematics is maybe draw a conclusion?

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

To be more precise, the answer is:

x = 1.18681439028098

(although I don’t guarantee the last few SFs.

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

Okay, this problem can be solved using algebraic methods in a way that you may find pleasing and diverting. Imagine you’re in a test with pencil and paper and a few minutes.
Give it a go at least.

is this another form 5 question or can anyone who graduated earlier than Terence Tao do it in their heads

dv said:

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

Okay, this problem can be solved using algebraic methods in a way that you may find pleasing and diverting. Imagine you’re in a test with pencil and paper and a few minutes.
Give it a go at least.

Does it involve carrying the one?

dv said:

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

Okay, this problem can be solved using algebraic methods in a way that you may find pleasing and diverting. Imagine you’re in a test with pencil and paper and a few minutes.
Give it a go at least.

OK, but don’t hold your breath.

(these things usually take me at least 3 days + 2 dog walks)

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

I suspect I’d have to resort to natural log function if done by hand.

dv said:

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

Okay, this problem can be solved using algebraic methods in a way that you may find pleasing and diverting. Imagine you’re in a test with pencil and paper and a few minutes.
Give it a go at least.

I think I knew how to do it once upon a time. But it’s probably about 50 years ago now.

sibeen said:

The Rev Dodgson said:

dv said:

Ah well hopefully Rev will have a go at it

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

I suspect I’d have to resort to natural log function if done by hand.

just pump wolframalpha

SCIENCE said:

sibeen said:

The Rev Dodgson said:

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

I suspect I’d have to resort to natural log function if done by hand.

just pump wolframalpha

Mine was from mathcad.

SCIENCE said:

sibeen said:

The Rev Dodgson said:

I did, and get the same answer as d-s (I suspect by the same method).

Successive approximations (using a well known spreadsheet program).

I suspect I’d have to resort to natural log function if done by hand.

just pump wolframalpha

spoiler alert

.

.

.

.

.

.

.

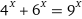
SCIENCE said:

SCIENCE said:

sibeen said:

I suspect I’d have to resort to natural log function if done by hand.

just pump wolframalpha

spoiler alert

.

.

.

.

.

.

.

Very sneaky :)

SCIENCE said:

is this another form 5 question or can anyone who graduated earlier than Terence Tao do it in their heads

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

Normal puns just make me go numb, but maths puns make me number.

Bunny_Fugger said:

Normal puns just make me go numb, but maths puns make me number.

debatable

Bunny_Fugger said:

Normal puns just make me go numb, but maths puns make me number.

Yeah good material, needs a bit of work on the delivery.
I’ve given it a 7.9.
The Russian Judge unexpectantly died last night.

Peak Warming Man said:

Bunny_Fugger said:

Normal puns just make me go numb, but maths puns make me number.

Yeah good material, needs a bit of work on the delivery.
I’ve given it a 7.9.
The Russian Judge unexpectantly died last night.

I for one consider that a worthy self-referential numerical punism.

Peak Warming Man said:

Bunny_Fugger said:

Normal puns just make me go numb, but maths puns make me number.

Yeah good material, needs a bit of work on the delivery.
I’ve given it a 7.9.
The Russian Judge unexpectantly died last night.

Old Age

dv said:

SCIENCE said:

is this another form 5 question or can anyone who graduated earlier than Terence Tao do it in their heads

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

When I were lad we did logarithms way before dipping our toes into the mysterious waters of calculus.

But then we had slide rules, so it may be all different now.

The Rev Dodgson said:

dv said:

SCIENCE said:

is this another form 5 question or can anyone who graduated earlier than Terence Tao do it in their heads

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

When I were lad we did logarithms way before dipping our toes into the mysterious waters of calculus.

But then we had slide rules, so it may be all different now.

so this is about lambda calculus now

dv said:

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

but anyway yes in fairness to dv apart from doing some other stuff just about now we agree we have found this kind of thing mildly entertaining before and if we hadn’t wasted our spare time on redactle then we would have tried to prime factorise the bases, rearrange to zero one side, and then look to see if it was some below-quintic polynomial amenable to algebraic solution

dv said:

diddly-squat said:

diddly-squat said:

that doesn;t look like it will be a very elegant solution

yuck.. what made you choose that?

x = 1.1868……..

Show working.

gack..

divide both sides by 8^x then simplify

(27/8)^x – (3/2)^x = 1 + (3/2)^x

simplify again

((3/2)^x)^3 – (3/2)^x = 1 + (3/2)^x

let (3/2)^x = n and simplify

n^3 – n = 1 + n

solve for n

(1) n = -1
(2) n = (1+5^½)/2
(3) n = (1-5^½)/2

substitute back in for n and solve for x

solution undefined for (1) and (3)

(3/2)^x = (1+5^½)/2

x = (ln(1+5^½)) / ln(3/2)

like I said.. gack

SCIENCE said:

dv said:

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

but anyway yes in fairness to dv apart from doing some other stuff just about now we agree we have found this kind of thing mildly entertaining before and if we hadn’t wasted our spare time on redactle then we would have tried to prime factorise the bases, rearrange to zero one side, and then look to see if it was some below-quintic polynomial amenable to algebraic solution

This place used to be fun like that. Now it’s all semantle this and proctologist that

diddly-squat said:

dv said:

diddly-squat said:

yuck.. what made you choose that?

x = 1.1868……..

Show working.

gack..

divide both sides by 8^x then simplify

(27/8)^x – (3/2)^x = 1 + (3/2)^x

simplify again

((3/2)^x)^3 – (3/2)^x = 1 + (3/2)^x

let (3/2)^x = n and simplify

n^3 – n = 1 + n

solve for n

(1) n = -1
(2) n = (1+5^½)/2
(3) n = (1-5^½)/2

substitute back in for n and solve for x

solution undefined for (1) and (3)

(3/2)^x = (1+5^½)/2

x = (ln(1+5^½)) / ln(3/2)

like I said.. gack

But what did you mean when you said gack?

diddly-squat said:

dv said:

diddly-squat said:

yuck.. what made you choose that?

x = 1.1868……..

Show working.

gack..

divide both sides by 8^x then simplify

(27/8)^x – (3/2)^x = 1 + (3/2)^x

simplify again

((3/2)^x)^3 – (3/2)^x = 1 + (3/2)^x

let (3/2)^x = n and simplify

n^3 – n = 1 + n

solve for n

(1) n = -1
(2) n = (1+5^½)/2
(3) n = (1-5^½)/2

substitute back in for n and solve for x

solution undefined for (1) and (3)

(3/2)^x = (1+5^½)/2

x = (ln(1+5^½)) / ln(3/2)

like I said.. gack

I love you, man

dv said:

diddly-squat said:

dv said:

Show working.

gack..

divide both sides by 8^x then simplify

(27/8)^x – (3/2)^x = 1 + (3/2)^x

simplify again

((3/2)^x)^3 – (3/2)^x = 1 + (3/2)^x

let (3/2)^x = n and simplify

n^3 – n = 1 + n

solve for n

(1) n = -1
(2) n = (1+5^½)/2
(3) n = (1-5^½)/2

substitute back in for n and solve for x

solution undefined for (1) and (3)

(3/2)^x = (1+5^½)/2

x = (ln(1+5^½)) / ln(3/2)

like I said.. gack

I love you, man

dv said:

SCIENCE said:

dv said:

You need to know how powers work, you need to know what a log is, you need to be able to solve a quadratic equation. I know half are you are going to say “we never did logarithms in Level Lambda when I was a lad” or whatever but it is a high school level maths problem, and when I encountered it I enjoyed working it out because there’s an “ahah!” aspect but maybe I’m the only one who enjoys that kind of thing.

but anyway yes in fairness to dv apart from doing some other stuff just about now we agree we have found this kind of thing mildly entertaining before and if we hadn’t wasted our spare time on redactle then we would have tried to prime factorise the bases, rearrange to zero one side, and then look to see if it was some below-quintic polynomial amenable to algebraic solution

This place used to be fun like that. Now it’s all semantle this and proctologist that

I’d sort it out for you but I have to clean the toilet.

On the bright side, SCIENCE’s comment made me look up specific solutions to quintic equations which led me to these fun facts:

For example, it has been shown that

x^5 – x – r=0

has solutions in radicals if and only if it has an integer solution or r is one of ±15, ±22440, or ±2759640, in which cases the polynomial is reducible.

And

About 1835, Jerrard demonstrated that quintics can be solved by using ultraradicals (also known as Bring radicals), the unique real root of t5 + t − a = 0 for real numbers a. In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

dv said:

On the bright side, SCIENCE’s comment made me look up specific solutions to quintic equations which led me to these fun facts:

For example, it has been shown that

x^5 – x – r=0

has solutions in radicals if and only if it has an integer solution or r is one of ±15, ±22440, or ±2759640, in which cases the polynomial is reducible.

And

About 1835, Jerrard demonstrated that quintics can be solved by using ultraradicals (also known as Bring radicals), the unique real root of t5 + t − a = 0 for real numbers a. In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I think you need to redefine your idea of “fun”

;)

dv said:

using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

The Rev Dodgson said:

dv said:

using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

yeah our Year 10 (¿Form 4?) mathematics teacher showed us how

The Rev Dodgson said:

dv said:

using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

The WP article covers it

https://en.m.wikipedia.org/wiki/Cubic_equation

I just tried it on Wolfram Alpha and got two different answers.

Firstly I swapped over the ‘-12ˣ’ to the other side, to get 27ˣ = 8ˣ + 24ˣ

WA got 1.49775
https://www.wolframalpha.com/input?i=27%5Ex%3D8%5Ex%2B24%5Ex

Then as the equation as written, 27ˣ -12ˣ = 8ˣ + 12ˣ and it came up with ….. something else.
https://www.wolframalpha.com/input?i=27%5Ex-12%5Ex%3D8%5Ex%2B12%5Ex

Shrug

Spiny Norman said:

I just tried it on Wolfram Alpha and got two different answers.

Firstly I swapped over the ‘-12ˣ’ to the other side, to get 27ˣ = 8ˣ + 24ˣ

WA got 1.49775
https://www.wolframalpha.com/input?i=27%5Ex%3D8%5Ex%2B24%5Ex

Shrug

But 12^x plus 12^x ain’t 24^x …

dv said:

Spiny Norman said:

I just tried it on Wolfram Alpha and got two different answers.

Firstly I swapped over the ‘-12ˣ’ to the other side, to get 27ˣ = 8ˣ + 24ˣ

WA got 1.49775
https://www.wolframalpha.com/input?i=27%5Ex%3D8%5Ex%2B24%5Ex

Shrug

But 12^x plus 12^x ain’t 24^x …

That would explain it.

dv said:

Spiny Norman said:

I just tried it on Wolfram Alpha and got two different answers.

Firstly I swapped over the ‘-12ˣ’ to the other side, to get 27ˣ = 8ˣ + 24ˣ

WA got 1.49775
https://www.wolframalpha.com/input?i=27%5Ex%3D8%5Ex%2B24%5Ex

Shrug

But 12^x plus 12^x ain’t 24^x …

slow down poindexter

you what now…??

SCIENCE said:

The Rev Dodgson said:

dv said:

using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

yeah our Year 10 (¿Form 4?) mathematics teacher showed us how

Was that before or after the advanced calculus?

dv said:

The Rev Dodgson said:

dv said:

using an approach similar to the more familiar approach of solving cubic equations by means of trigonometric functions.

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

The WP article covers it

https://en.m.wikipedia.org/wiki/Cubic_equation

Thanks, I’ll have a read.

buffy said:

Witty Rejoinder said:

It’s the math vs maths that is irking Buffy.

Of course. It is either math. (with the full stop to indicate you have shortened it). Or it is “maths” (which is a contraction and doesn’t need the full stop). And Mr. is also wrong and irksome. It doesn’t need that full stop.

Mr. Math – Making the World a Math-ier Place!

https://www.mrmath.com/

diddly-squat said:

dv said:

Spiny Norman said:

I just tried it on Wolfram Alpha and got two different answers.

Firstly I swapped over the ‘-12ˣ’ to the other side, to get 27ˣ = 8ˣ + 24ˣ

WA got 1.49775
https://www.wolframalpha.com/input?i=27%5Ex%3D8%5Ex%2B24%5Ex

Shrug

But 12^x plus 12^x ain’t 24^x …

slow down poindexter

you what now…??

sure it is when x = 1 oh wait

fsm said:

buffy said:

Witty Rejoinder said:

It’s the math vs maths that is irking Buffy.

Of course. It is either math. (with the full stop to indicate you have shortened it). Or it is “maths” (which is a contraction and doesn’t need the full stop). And Mr. is also wrong and irksome. It doesn’t need that full stop.

Mr. Math – Making the World a Math-ier Place!

https://www.mrmath.com/

exactly, nobody cares what pronouns pronumerals they use

SCIENCE said:

diddly-squat said:

dv said:

But 12^x plus 12^x ain’t 24^x …

slow down poindexter

you what now…??

sure it is when x = 1 oh wait

Or 0 I guess?

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

The WP article covers it

https://en.m.wikipedia.org/wiki/Cubic_equation

Thanks, I’ll have a read.

As the only person in the known universe who uses algebraic solutions to cubic and quartic equations to find the neutral axis depth of reinforced concrete sections, I can’t think why I didn’t look at this before.

The Rev Dodgson said:

The Rev Dodgson said:

dv said:

The WP article covers it

https://en.m.wikipedia.org/wiki/Cubic_equation

Thanks, I’ll have a read.

As the only person in the known universe who uses algebraic solutions to cubic and quartic equations to find the neutral axis depth of reinforced concrete sections, I can’t think why I didn’t look at this before.

Because it wasn’t reinforced concrete?

The Rev Dodgson said:

The Rev Dodgson said:

dv said:

The WP article covers it

https://en.m.wikipedia.org/wiki/Cubic_equation

Thanks, I’ll have a read.

As the only person in the known universe who uses algebraic solutions to cubic and quartic equations to find the neutral axis depth of reinforced concrete sections, I can’t think why I didn’t look at this before.

Well now you can use your ultraradicals to solve the quintics

dv said:

The Rev Dodgson said:

The Rev Dodgson said:

Thanks, I’ll have a read.

As the only person in the known universe who uses algebraic solutions to cubic and quartic equations to find the neutral axis depth of reinforced concrete sections, I can’t think why I didn’t look at this before.

Well now you can use your ultraradicals to solve the quintics

I think that might be going a bit too far :)

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

So, by numerical methods does that mean I cannot use mathcad?

kicks dirt

sibeen said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

So, by numerical methods does that mean I cannot use mathcad?

kicks dirt

Christ, I’m a sap, 30 seconds after posting that I’m looking at it and trying some numbers in my head.

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

22

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

I suspect that 118 having so few divisors will be a key.

1, 2, 59, 118.

But that’s doing something numerical, so I’ve probably cheated.

sibeen said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

I suspect that 118 having so few divisors will be a key.

1, 2, 59, 118.

But that’s doing something numerical, so I’ve probably cheated.

As in, being key, it gives the answer.

62.

sibeen said:

sibeen said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

I suspect that 118 having so few divisors will be a key.

1, 2, 59, 118.

But that’s doing something numerical, so I’ve probably cheated.

As in, being key, it gives the answer.

62.

Err, that’s wrong.

sibeen said:

sibeen said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

So, by numerical methods does that mean I cannot use mathcad?

kicks dirt

Christ, I’m a sap, 30 seconds after posting that I’m looking at it and trying some numbers in my head.

Heh

Kingy said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

22

winner winner

dv said:

Kingy said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

22

winner winner

Hmm. This appears to somehow work without using my completely insightful comment about the lack of divisors. It must be wrong – damnit.

OK – thinks about other tricks.

dv said:

Kingy said:

dv said:

Have a go at this without using brute force or numerical methods etc. There’s a trick.

x and y are positive integers.

x + xy + y = 118

What is x + y?

22

winner winner

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Kingy said:

dv said:

Kingy said:

22

winner winner

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

dv said:

Kingy said:

dv said:

winner winner

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

OTOAI?

dv said:

Kingy said:

dv said:

winner winner

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

Yeah, not getting how you end up with 6 + 16 = 22 out of the above.

Kingy said:

dv said:

Kingy said:

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

OTOAI?

Other than one and itself

sibeen said:

dv said:

Kingy said:

I don’t know what the trick is, I just tried a few combinations in my head and got lucky. That still counts though, right?

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

Yeah, not getting how you end up with 6 + 16 = 22 out of the above.

(x + 1)(y + 1) = 119

Given the two factors are 7 and 17, we can say x+1=7 and y+1=17 (or vice versa)

So x = 6 and y = 16 (or vice versa)

dv said:

Kingy said:

dv said:

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

OTOAI?

Other than one and itself

Ahhh….

dv said:

sibeen said:

dv said:

Okay
I guess the trick is
x + xy + y = 118
(x + 1)(y + 1) = 119
119 only has two factors OTOAI

Yeah, not getting how you end up with 6 + 16 = 22 out of the above.

(x + 1)(y + 1) = 119

Given the two factors are 7 and 17, we can say x+1=7 and y+1=17 (or vice versa)

So x = 6 and y = 16 (or vice versa)

So, 119 has four factors, just like 118…I was this > < fucking close!

sibeen said:

dv said:

sibeen said:

Yeah, not getting how you end up with 6 + 16 = 22 out of the above.

(x + 1)(y + 1) = 119

Given the two factors are 7 and 17, we can say x+1=7 and y+1=17 (or vice versa)

So x = 6 and y = 16 (or vice versa)

So, 119 has four factors, just like 118…I was this > < fucking close!

Okay, but the reason it can’t be 1 and 119 is that would mean x = 0 and I specified positive

dv said:

sibeen said:

dv said:

(x + 1)(y + 1) = 119

Given the two factors are 7 and 17, we can say x+1=7 and y+1=17 (or vice versa)

So x = 6 and y = 16 (or vice versa)

So, 119 has four factors, just like 118…I was this > < fucking close!

Okay, but the reason it can’t be 1 and 119 is that would mean x = 0 and I specified positive

Yeah, I get that, I was just pointing out that my idea of factors came into play and therefore I was this ><- fucking close.

In fact, I’m claiming the win. I said it first.

sibeen said:

dv said:

sibeen said:

So, 119 has four factors, just like 118…I was this > < fucking close!

Okay, but the reason it can’t be 1 and 119 is that would mean x = 0 and I specified positive

Yeah, I get that, I was just pointing out that my idea of factors came into play and therefore I was this ><- fucking close.

In fact, I’m claiming the win. I said it first.

Yes you were on the right track

The Rev Dodgson said:

SCIENCE said:

The Rev Dodgson said:

I wouldn’t say that solving cubics using trig functions was that familiar.

Got a ref?

yeah our Year 10 (¿Form 4?) mathematics teacher showed us how

Was that before or after the advanced calculus?

before, officially speaking

The Rev Dodgson said:

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Having now looked at my original code, it also uses a trigonometric method, similar in principle to the current TATE article, but with several differences in detail. For more detail of the original code see:
https://newtonexcelbach.com/2010/08/04/solving-cubic-and-quartic-equations-with-excel/
That says I used the same method as:
https://www.excelcalcs.com/calcs/repository/maths/polynom.xls/

but actually it isn’t.

So I’m not sure where my original superfast code came from, but I think I’ll stick with it.

The Rev Dodgson said:

The Rev Dodgson said:

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Having now looked at my original code, it also uses a trigonometric method, similar in principle to the current TATE article, but with several differences in detail. For more detail of the original code see:
https://newtonexcelbach.com/2010/08/04/solving-cubic-and-quartic-equations-with-excel/
That says I used the same method as:
https://www.excelcalcs.com/calcs/repository/maths/polynom.xls/

but actually it isn’t.

So I’m not sure where my original superfast code came from, but I think I’ll stick with it.

So you didn’t write it?

sibeen said:

The Rev Dodgson said:

The Rev Dodgson said:

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Having now looked at my original code, it also uses a trigonometric method, similar in principle to the current TATE article, but with several differences in detail. For more detail of the original code see:
https://newtonexcelbach.com/2010/08/04/solving-cubic-and-quartic-equations-with-excel/
That says I used the same method as:
https://www.excelcalcs.com/calcs/repository/maths/polynom.xls/

but actually it isn’t.

So I’m not sure where my original superfast code came from, but I think I’ll stick with it.

So you didn’t write it?

Yes, I did write the code, but I’m pretty sure I didn’t come up with the solution method myself.

The Rev Dodgson said:

The Rev Dodgson said:

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Having now looked at my original code, it also uses a trigonometric method, similar in principle to the current TATE article, but with several differences in detail. For more detail of the original code see:
https://newtonexcelbach.com/2010/08/04/solving-cubic-and-quartic-equations-with-excel/
That says I used the same method as:
https://www.excelcalcs.com/calcs/repository/maths/polynom.xls/

but actually it isn’t.

So I’m not sure where my original superfast code came from, but I think I’ll stick with it.

Good

dv said:

The Rev Dodgson said:

The Rev Dodgson said:

I have now set up an Excel VBA UDF to solve cubic equations using the trigonometric or hyperbolic methods.

It all seems to work quite neatly, but for some reason it takes 2-3 times longer to run than my previous code.

I also found:
https://www.researchgate.net/publication/326697976_TRIGONOMETRIC_SOLUTION_TO_THE_CUBIC_EQUATION

I think it’s just the same information as in the Wikipedia article, but I’ve only glanced at it so far.

Having now looked at my original code, it also uses a trigonometric method, similar in principle to the current TATE article, but with several differences in detail. For more detail of the original code see:
https://newtonexcelbach.com/2010/08/04/solving-cubic-and-quartic-equations-with-excel/
That says I used the same method as:
https://www.excelcalcs.com/calcs/repository/maths/polynom.xls/

but actually it isn’t.

So I’m not sure where my original superfast code came from, but I think I’ll stick with it.

Good

Further research reveals that the methods used in my original code came from Numerical Recipes in C, and the NR in C web site is still going.

Those wanting a nostalgic reminder of what the Internet used to look like in the Good Old Days may like to visit:

Numerical Recipes

And you can read the book at:

Numerical Recipes

ooh we’re almost certain we had a flick through that novel in our earlier journeys thanks

The Rev Dodgson said:

And you can read the book at:

Numerical Recipes

And with further further research I found:
https://github.com/LuaDist/gsl/blob/master/poly/solve_cubic.c

which is even closer to my VBA code (and can be accessed without annoying pop-ups).

The Rev Dodgson said:

The Rev Dodgson said:

And you can read the book at:

Numerical Recipes

And with further further research I found:
https://github.com/LuaDist/gsl/blob/master/poly/solve_cubic.c

which is even closer to my VBA code (and can be accessed without annoying pop-ups).

… and documentation (and links to other polynomial related code) at:
https://www.gnu.org/software/gsl/doc/html/poly.html

The Rev Dodgson said:

The Rev Dodgson said:

The Rev Dodgson said:

And you can read the book at:

Numerical Recipes

And with further further research I found:
https://github.com/LuaDist/gsl/blob/master/poly/solve_cubic.c

which is even closer to my VBA code (and can be accessed without annoying pop-ups).

… and documentation (and links to other polynomial related code) at:
https://www.gnu.org/software/gsl/doc/html/poly.html

ah, plagiarism