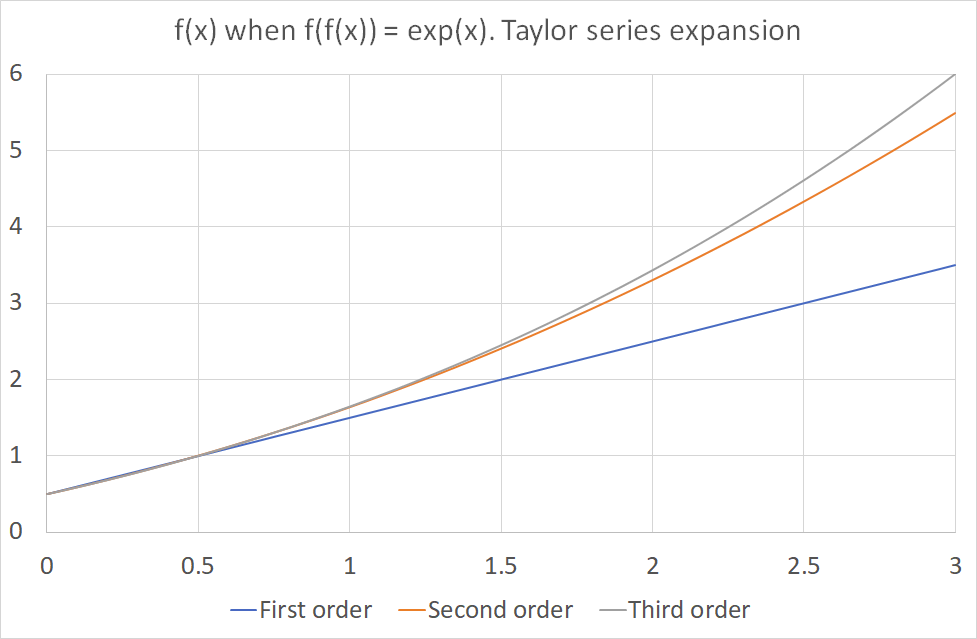
Recently it was asked by mollwolfumble: what is the name of the special function g(x) such that g(g(x)) = exp(x).

I said that there an an infinite number of such functions but did not elaborate, so here are some more details.

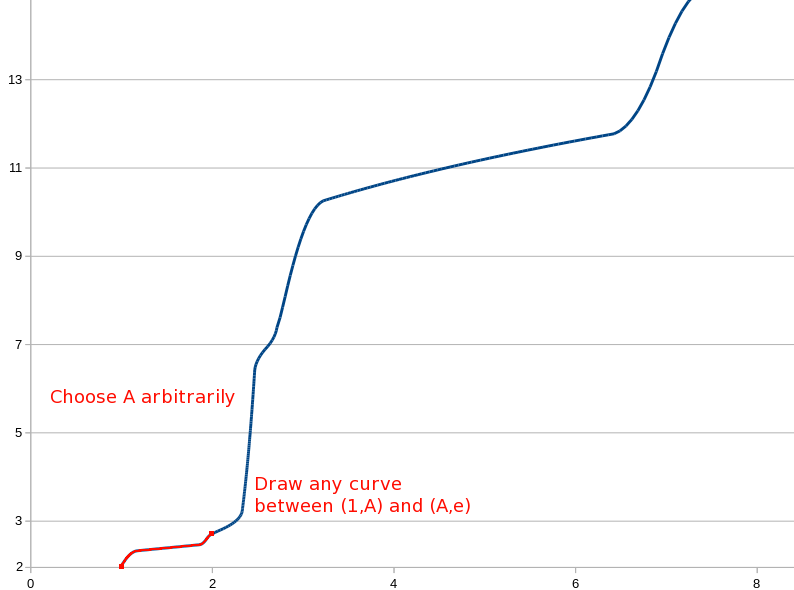
Under such a function, if g(1) = A, then g(A) = e.

We can arbitrarily pick an A. Let’s say:

g(1) = 2, so g(2) = e

We can now pretty much arbitrarily define values of g for values of x from 1 to 2.
Note that exp(x) increases monotonically and this goes much easier if we choose g(x) such that it also does and does not exceed exp(x).

g(1.25) = 2.3, so g(2.3) = 3.4903…
g(1.8) = 2.6, so g(2.6) = 6.0496…

Now if I desire this to be a continuous function then I’ll make sure that as x->2, g(x) approached e.
g(1.99) = 2.7, so g(2.7) = 7.3155…

And if I require other kinds of smoothness at the bounds (for instance, require continuous derivatives) then I can also allow for that. In so doing, we have also created the function over the domain from a to e, and by extension the rest of the infinite domain.

So that’s basically it. Choose a value A so that g(1) = A and g(A) = e, and then you have a free hand to draw a function over the domain from 1 to A, which will then propagate over the infinite domain.

As well as for exp(x), this trick should work for any other “well-behaved” monotonic function.

Yes.

But I want the unique answer. The one true special function that is as smooth as possible.

I’m trying to think of an illustration. It escapes me for the moment.

Perhaps this will suffice. The famous Gamma function satisfies Gamma(n+1) = Gamma(n) * n. So, choose an arbitrary curve between 1 and 2 and apply the recurrence relationship to generate an arbitrary Gamma function. But that is wrong because there’s only one Gamma function not arbitrarily many of them.

I suspect that there is some way to define a special function as a limit of ordinary functions. I had a go at this with f(f(X))=ln(X). This has to be between ln(x)^n and x^1/n for arbitrarily large n. I don’t know if I succeeded. It seemed to work for n=10^300, but I didn’t follow it up. The other possibility is to find a definition of these special functions as a Taylor series, or as an integral.

Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves. You may be chasing a phantasm.

dv said:

Recently it was asked by mollwolfumble: what is the name of the special function g(x) such that g(g(x)) = exp(x).

I said that there an an infinite number of such functions but did not elaborate, so here are some more details.

Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves. You may be chasing a phantasm.

> Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves

Agree.

How about this?

The function I’m looking for has the following properties.

a) g(g(x)) = exp(x)

b) d^n g(x) / dx^n is monotonic for all n

I think that that is true for log(x). If not then I’ll have to rethink it.

dv said:

Recently it was asked by mollwolfumble: what is the name of the special function g(x) such that g(g(x)) = exp(x).

I said that there an an infinite number of such functions but did not elaborate, so here are some more details.

Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves. You may be chasing a phantasm.

> Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves

Agree. Actually, well done! I got to that and found myself stuck. Now I’m progressing beyond it.

How about this?

The function I’m looking for has the following properties.

a) g(g(x)) = exp(x)

b) d^n g(x) / dx^n is monotonic for all n

It ought to be possible to get a single definitive answer using Taylor series.

exp(x) = 1 + x + x^2/2 + x^3/6 + …

f(f(x)) = 1 + x gives
f(x) = 0.5 + x

f(f(x)) = 1 + x + x^2/2 (to second order).
gives f(x) = 0.465772 + 0.885672 x + 0.261301 x^2

At each order n of Taylor series for f(f(x)) = exp(x)
we get n equations in n unknowns for the Taylor series of f(x)

Keep the process going until we get the infinitely differentiable Taylor series for f(x) where f(f(x)) = exp(x).

:-)

mollwollfumble said:

dv said:

Recently it was asked by mollwolfumble: what is the name of the special function g(x) such that g(g(x)) = exp(x).

I said that there an an infinite number of such functions but did not elaborate, so here are some more details.

Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves. You may be chasing a phantasm.

> Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves

Agree. Actually, well done! I got to that and found myself stuck. Now I’m progressing beyond it.

How about this?

The function I’m looking for has the following properties.

a) g(g(x)) = exp(x)

b) d^n g(x) / dx^n is monotonic for all n

It ought to be possible to get a single definitive answer using Taylor series.

exp(x) = 1 + x + x^2/2 + x^3/6 + …

f(f(x)) = 1 + x gives
f(x) = 0.5 + x

f(f(x)) = 1 + x + x^2/2 (to second order).
gives f(x) = 0.465772 + 0.885672 x + 0.261301 x^2

At each order n of Taylor series for f(f(x)) = exp(x)
we get n equations in n unknowns for the Taylor series of f(x)

Keep the process going until we get the infinitely differentiable Taylor series for f(x) where f(f(x)) = exp(x).

:-)

First, second and third order solutions for f(f(x))=exp(x) using Taylor’s series.

First order
f(x) = 0.5 + x

Second order
f(x) = 0.497894 + 0.878111 x + 0.2618 x^2

Third order
f(x) = 0.498574 + 0.876383 x + 0.247388 x^2 + 0.0261216 x^3

Looks like it’s working beautifully.

mollwollfumble said:

dv said:

Recently it was asked by mollwolfumble: what is the name of the special function g(x) such that g(g(x)) = exp(x).

I said that there an an infinite number of such functions but did not elaborate, so here are some more details.

Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves. You may be chasing a phantasm.

> Even among those that are “smooth as possible”, ie continuous is all derivatives, there are still an infinite set of possible curves

Agree. Actually, well done! I got to that and found myself stuck. Now I’m progressing beyond it.

How about this?

The function I’m looking for has the following properties.

a) g(g(x)) = exp(x)

b) d^n g(x) / dx^n is monotonic for all n

It ought to be possible to get a single definitive answer using Taylor series.

exp(x) = 1 + x + x^2/2 + x^3/6 + …

f(f(x)) = 1 + x gives
f(x) = 0.5 + x

f(f(x)) = 1 + x + x^2/2 (to second order).
gives f(x) = 0.465772 + 0.885672 x + 0.261301 x^2

At each order n of Taylor series for f(f(x)) = exp(x)
we get n equations in n unknowns for the Taylor series of f(x)

Keep the process going until we get the infinitely differentiable Taylor series for f(x) where f(f(x)) = exp(x).

:-)

First, second and third order solutions for f(f(x))=exp(x) using Taylor’s series.

First order
f(x) = 0.5 + x

Second order
f(x) = 0.497894 + 0.878111 x + 0.2618 x^2

Third order
f(x) = 0.498574 + 0.876383 x + 0.247388 x^2 + 0.0261216 x^3

Looks like it’s working beautifully.

nice

SCIENCE said:

nice

cheers

dv said:

SCIENCE said:

nice

cheers

Special functions, can they be likened to Poo-tin’s special operational functions?

roughbarked said:

dv said:

SCIENCE said:

nice

cheers

Special functions, can they be likened to Poo-tin’s special operational functions?

there might be turning points but not if they’re monotonic

SCIENCE said:

roughbarked said:

dv said:

cheers

Special functions, can they be likened to Poo-tin’s special operational functions?

there might be turning points but not if they’re monotonic

I’m far from sure that monotonic derivatives of all orders are good enough.

Take e^x + sin x for example.

For x above ten or so all derivatives of all orders exist and are monotonic, but it does have a fluctuating component.

The Taylor series method should work, though. At least work for the half-exponential function.