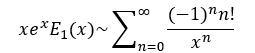It just occurred to me that the famous proof that omega is the smallest infinite number can be destroyed by a ‘reductio ad absurdum’, reduce to the absurd limit. The proof that omega is the smallest infinite number goes like this.
- Omega is defined as the set of all finite natural numbers. Therefore any number smaller than omega is a finite natural number.
The absurd reduction is this.
- Two is defined as the set containing only zero and one. Therefore the only numbers smaller than two are zero and one.
-
The Rev Dodgson said:
mollwollfumble said:
Posted “Part 1 to 8. Just the slides https://youtu.be/t5sXzM64hXg” to both Physics forum and a philosopher from Monash Uni today.
I don’t know if I have the Monash email correct.
The last two times I tried posting this stuff to physics forum, it was rejected by the forum moderator before it ever appeared on the forum. I don’t have much hope for third time, but they’re the people who could benefit from this the most. They’re the people who need to know.
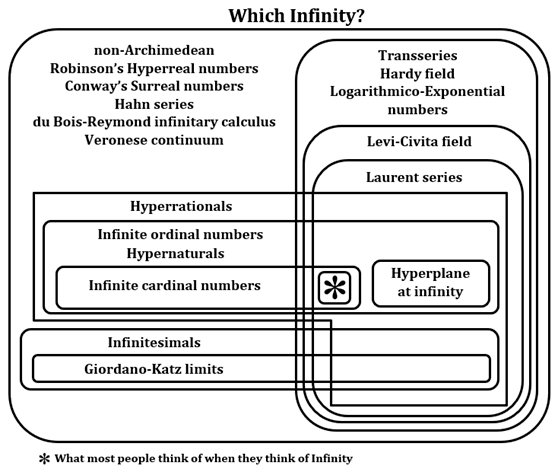
What do you see of the physical significance of all these infinities?
Do you mean all the infinite numbers from ordinal infinity? Or all the different systems of infinite numbers?
For all the different numbers from ordinal infinity, I see them as the limits of functions. Using omega for infinity:
The limit as x tends to omega of f(x) is f(omega).
So f(x)=x tends to omega.
f(x)=x^2 tends to omega squared.
f(x)=exp(x) tends to e to the power omega.
etc. All are different values of infinity.
Another application of multiple values of infinity is in the paradox of Achilles and the tortoise.
Say that Achilles takes one step to catch up to where the tortoise has been. Then another step to catch up to where the tortoise has moved during the first step. After an infinite number of steps Achilles has caught up to the tortoise. So Achilles can’t finish the race, because he can never pass the tortoise, he can only catch up to it.
In order to finish the race, we need a second value for infinity much larger than the first. And it turns out that e to the power omega fits the bill. It’s a second and larger value of infinity that will allow Achilles to finish the race.
In terms of why there are so many different systems of infinite numbers. I see these as equivalence classes. Going back to the natural numbers, starting with zero this time. Let’s separate the natural numbers into the evens (0,2,4,6,8,…) and the odds (1,3,5,7,9,…). Applying these equivalence classes to the natural numbers reduces the total number of numbers to two, 0 and 1, binary notation.
So, starting with the infinite ordinal numbers.
Infinity plus an infinitesimal is a new number.
I can apply an equivalence class to that which says that an infinitesimal is so small relative to infinity that we can ignore the change. This is what I call reducing the resolution.
If I reduce the resolution so much that e to the power infinity is a new number but infinity squared is not, then we get back exactly to the cardinal infinity of standard analysis.
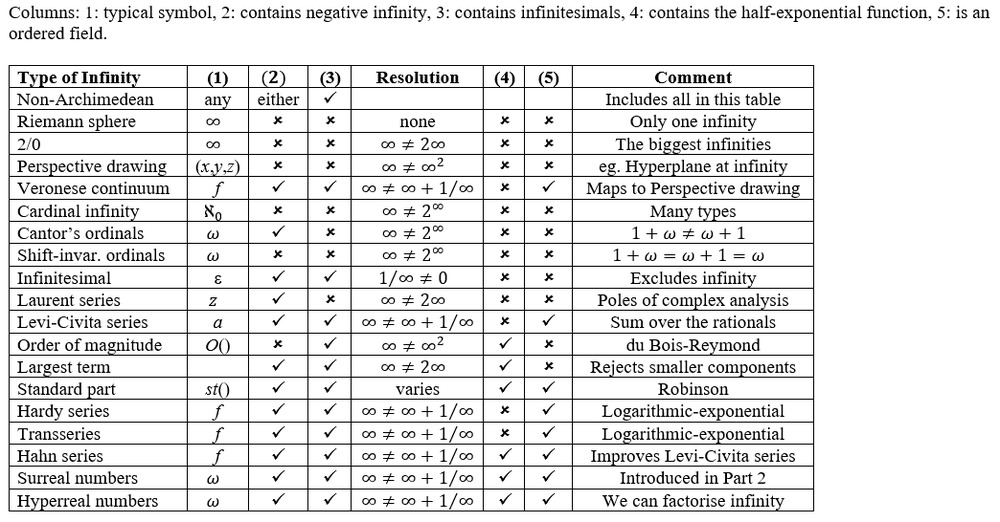
Applying equivalent classes to ordinal infinity generates a total of five different systems of infinite numbers. Other systems of infinite numbers come about by dropping “generators”. For instance if I exclude the special function f(f(x))=exp(x) then the collection of infinite numbers reduces back to the logarithmic-exponential numbers.
Or if I make addition non-commutative x=1+x≠x+1 then it reduces to Cantor’s ordinal infinity.
And then there are different systems of infinite numbers that are essentially the same, but defined in a different way. Defined using a number is a set, or a Dedekind cut, or a function, or a sequence/series, or a geometrical/topological transformation, or a continuum, or in calculus dy/dx.
Answer the question?