A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

KJW said:

A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

OK, so getting from 16 to 31 is pretty simple and straightforward, once you know how to do it.

Hadn’t seen that before (that I remember!)

we’re sure an argument could be had as to what an appropriate measure of “simple” is but there may be something to do with optimality and being the simplest

KJW said:

A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

Yep. I know both answers. The answer 31 also comes from a polynomial fit.

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

I use something like this in my Devil’s Puzzle Book, where I ask what is the next number in the sequence 1,2,3,4,5,…

mollwollfumble said:

KJW said:

A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

Yep. I know both answers. The answer 31 also comes from a polynomial fit.

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

I use something like this in my Devil’s Puzzle Book, where I ask what is the next number in the sequence 1,2,3,4,5,…

So if we have:
x = 1,2,3,…n
and
y = 1, 2, 4,…2^(n-1)

and we fit a polynomial of order n-1 to those numbers, it seems that the next number in the sequence is always 2^n-1.

I’ll leave it to someone else to prove that :)

There’s a very easy way to continue the sequence
1,2,4,8,16,31…
It’s called “divided differences”
Take the difference between each pair of numbers, and repeat.

1,2,4,8,16,31
1,2,4,8,15
1,2,4,7
1,2,3

Then extend the sequence and reverse the process.

1,2,3,4,5,6,…
1,2,4,7,11,16,22,…
1,2,4,8,15,26,42,64,…
1,2,4,8,16,31,57,99,163,…

Back in the dim distant past I found it very useful in answering certain questions in IQ tests.

The Rev Dodgson said:

mollwollfumble said:

KJW said:

A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

Yep. I know both answers. The answer 31 also comes from a polynomial fit.

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

I use something like this in my Devil’s Puzzle Book, where I ask what is the next number in the sequence 1,2,3,4,5,…

So if we have:
x = 1,2,3,…n
and
y = 1, 2, 4,…2^(n-1)

and we fit a polynomial of order n-1 to those numbers, it seems that the next number in the sequence is always 2^n-1.

I’ll leave it to someone else to prove that :)

so you all agree that doubling each time until proven otherwise seems to be the simplest unifying

The Rev Dodgson said:

mollwollfumble said:

KJW said:

A few days ago, I caught the end of a part of the TV program “QI” which dealt with the sequence: 1, 2, 4, 8, 16, …

As I didn’t see most of it, I can only assume that they asked what the next number in the sequence is. Naturally, in typical QI style, the incorrect answer is 32. The “correct” answer is 31. This answer is based on the sequence given by dividing a circle into areas. The host pointed out that there is insufficient information to provide the next number in this sequence and that the correct answer depends on the question asked.

Yep. I know both answers. The answer 31 also comes from a polynomial fit.

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

I use something like this in my Devil’s Puzzle Book, where I ask what is the next number in the sequence 1,2,3,4,5,…

So if we have:
x = 1,2,3,…n
and
y = 1, 2, 4,…2^(n-1)

and we fit a polynomial of order n-1 to those numbers, it seems that the next number in the sequence is always 2^n-1.

I’ll leave it to someone else to prove that :)

so you all agree that doubling each time until proven otherwise seems to be the simplest unifying

twice

SCIENCE said:

so you all agree that doubling each time until proven otherwise seems to be the simplest unifying

Nope. See my post above.

mollwollfumble said:

There’s a very easy way to continue the sequence
1,2,4,8,16,31…
It’s called “divided differences”
Take the difference between each pair of numbers, and repeat.

1,2,4,8,16,31
1,2,4,8,15
1,2,4,7
1,2,3

Then extend the sequence and reverse the process.

1,2,3,4,5,6,…
1,2,4,7,11,16,22,…
1,2,4,8,15,26,42,64,…
1,2,4,8,16,31,57,99,163,…

Back in the dim distant past I found it very useful in answering certain questions in IQ tests.

That’s weird. Powers of 2 appear in the polynomial sequences as well.
As in.
1,2,.,4
1,2,4,.,.,16
1,2,4,8,.,.,.,64
1,2,4,8,16,.,.,.,.,256
Etc.

mollwollfumble said:

SCIENCE said:

so you all agree that doubling each time until proven otherwise seems to be the simplest unifying

Nope. See my post above.

seems more complicated than “ *2 “ but hey not everyone’s a rabbit

SCIENCE said:

mollwollfumble said:

SCIENCE said:

so you all agree that doubling each time until proven otherwise seems to be the simplest unifying

Nope. See my post above.

seems more complicated than “ *2 “ but hey not everyone’s a rabbit

OK, but we are not looking for the simplest one.

We are looking for any method that has a reasonably simple and consistent procedure, but gives a different answer to the simplest one.

This is considered to be qi on QI, and who are we to argue with them?

The Rev Dodgson said:

SCIENCE said:

mollwollfumble said:

Nope. See my post above.

seems more complicated than “ *2 “ but hey not everyone’s a rabbit

OK, but we are not looking for the simplest one.

We are looking for any method that has a reasonably simple and consistent procedure, but gives a different answer to the simplest one.

This is considered to be qi on QI, and who are we to argue with them?

no worries they’ve got it sorted*

https://oeis.org/

*: not sure about the sort order though

like

Number of divisors of n!.

(offset 1) a(0) = 1, a(n) = sum of digits of all previous terms.

and that’s just the first 2 pages

SCIENCE said:

like

Number of divisors of n!.

(offset 1) a(0) = 1, a(n) = sum of digits of all previous terms.

a(n) = Sum_{k=0..5} C(n,k). Number of different resistances that can be obtained by combining n one-ohm resistors. a(0) = 1; thereafter a(n) is obtained by applying the “delete multiple digits” map m -> A320485 to 2*a(n-1). The number of odd partitions of consecutive odd integers. Number of configurations of the sliding block 8-puzzle that require a minimum of n moves to be reached, starting with the empty square in one of the corners.

and that’s just the first 2 pages

SCIENCE said:

SCIENCE said:

like

Number of divisors of n!.

(offset 1) a(0) = 1, a(n) = sum of digits of all previous terms.

a(n) = Sum_{k=0..5} C(n,k). Number of different resistances that can be obtained by combining n one-ohm resistors. a(0) = 1; thereafter a(n) is obtained by applying the “delete multiple digits” map m -> A320485 to 2*a(n-1). The number of odd partitions of consecutive odd integers. Number of configurations of the sliding block 8-puzzle that require a minimum of n moves to be reached, starting with the empty square in one of the corners.

and that’s just the first 2 pages

like

Number of divisors of n!.

(offset 1) a(0) = 1, a(n) = sum of digits of all previous terms. 

 a(n) = Sum_{k=0..5} C(n,k). 

 Number of different resistances that can be obtained by combining n one-ohm resistors. 

 a(0) = 1; thereafter a(n) is obtained by applying the "delete multiple digits" map m -> A320485(m) to 2*a(n-1). 

 The number of odd partitions of consecutive odd integers. 

 Number of configurations of the sliding block 8-puzzle that require a minimum of n moves to be reached, starting with the empty square in one of the corners. 

and that's just the first 2 pages

and the beat goes on

SCIENCE said:

The Rev Dodgson said:

SCIENCE said:

seems more complicated than “ *2 “ but hey not everyone’s a rabbit

OK, but we are not looking for the simplest one.

We are looking for any method that has a reasonably simple and consistent procedure, but gives a different answer to the simplest one.

This is considered to be qi on QI, and who are we to argue with them?

no worries they’ve got it sorted*

https://oeis.org/

*: not sure about the sort order though

I might have missed it, because I haven’t got the Latin for following all this stuff, but they didn’t seem to have moll’s sequence there.

The Rev Dodgson said:

SCIENCE said:

The Rev Dodgson said:

OK, but we are not looking for the simplest one.

We are looking for any method that has a reasonably simple and consistent procedure, but gives a different answer to the simplest one.

This is considered to be qi on QI, and who are we to argue with them?

no worries they’ve got it sorted*

https://oeis.org/

*: not sure about the sort order though

I might have missed it, because I haven’t got the Latin for following all this stuff, but they didn’t seem to have moll’s sequence there.

He might have confused QI for IQ?

roughbarked said:

The Rev Dodgson said:

SCIENCE said:

no worries they’ve got it sorted*

https://oeis.org/

*: not sure about the sort order though

I might have missed it, because I haven’t got the Latin for following all this stuff, but they didn’t seem to have moll’s sequence there.

He might have confused QI for IQ?

I think both of the people who have sat at the top table on QI have a pretty high IQ.

Some of the contestants perhaps not so much :)

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

I might have missed it, because I haven’t got the Latin for following all this stuff, but they didn’t seem to have moll’s sequence there.

He might have confused QI for IQ?

I think both of the people who have sat at the top table on QI have a pretty high IQ.

Some of the contestants perhaps not so much :)

From this I am sure you garnered my content.

roughbarked said:

The Rev Dodgson said:

roughbarked said:

He might have confused QI for IQ?

I think both of the people who have sat at the top table on QI have a pretty high IQ.

Some of the contestants perhaps not so much :)

From this I am sure you garnered my content.

No, no-eyed deer. :)

The Rev Dodgson said:

SCIENCE said:

The Rev Dodgson said:

OK, but we are not looking for the simplest one.

We are looking for any method that has a reasonably simple and consistent procedure, but gives a different answer to the simplest one.

This is considered to be qi on QI, and who are we to argue with them?

no worries they’ve got it sorted*

https://oeis.org/

*: not sure about the sort order though

I might have missed it, because I haven’t got the Latin for following all this stuff, but they didn’t seem to have moll’s sequence there.

surely that’s because if you’re correct earlier then it’s a more general result not specific to the particular number (5) of terms given

mollwollfumble said:

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

KJW said:

mollwollfumble said:

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

The Rev Dodgson said:

KJW said:

mollwollfumble said:

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

Surely a gentleman of your talents can set out to prove that it is true for nth order polynomials generally.

dv said:

The Rev Dodgson said:

KJW said:

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

Surely a gentleman of your talents can set out to prove that it is true for nth order polynomials generally.

I’d probably get there eventually, but there are several people here who I’m sure would do it much more efficiently.

Anyway, I have things of greater moment to investigate just now. (best way to calculate secondary bending moments due to pre-stressing an indeterminant structure).

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

Surely a gentleman of your talents can set out to prove that it is true for nth order polynomials generally.

I’d probably get there eventually, but there are several people here who I’m sure would do it much more efficiently.

No worries.

The Rev Dodgson said:

KJW said:

mollwollfumble said:

If we fit a quartic (4th order) polynomial to 1,2,4,8,16 then the next number is 31.

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

I can’t speak about moll’s procedure for fitting a polynomial to a number of points, but fitting polynomials to points is something I’ve done in Excel (VBA) a number of years ago. The point I was making was that because the fitting of 5 points to a quartic polynomial (or in general, fitting n points to an (n–1)-th degree polynomial) is unique, if the 5 points are the values 1,2,4,8,16, then the quartic polynomial must be ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1, the same polynomial as the number of areas of the circle, in which case the next number is 31.

KJW said:

The Rev Dodgson said:

KJW said:

That’s interesting. However, because the formula for the number of areas of the circle is the quartic polynomial:

ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1

and fitting five points to a quartic polynomial uniquely specifies the quartic polynomial, 31 is the only number the next number could be.

But, if we fit to a quintic polynomial, we can fit 1,2,4,8,16, and an arbitrarily chosen sixth number.

But moll’s procedure of fitting a polynomial to a number of points then using that to calculate the next step always seems to result in 1 less than doubling for the last step, at least up to 7th order polynomials, so it seems more general than the number of triangles in a circle thing.

I can’t speak about moll’s procedure for fitting a polynomial to a number of points, but fitting polynomials to points is something I’ve done in Excel (VBA) a number of years ago. The point I was making was that because the fitting of 5 points to a quartic polynomial (or in general, fitting n points to an (n–1)-th degree polynomial) is unique, if the 5 points are the values 1,2,4,8,16, then the quartic polynomial must be ƒ(n) = n(n³ – 6n² + 23n – 18)/24 + 1, the same polynomial as the number of areas of the circle, in which case the next number is 31.

Agreed.
The form of the lowest order polynomials that fit the first n points in the doubled series is quite interesting. I’ll post my results tomorrow (going to sleep now).

I have now fitted polynomials of the form:
Y = C + (ax + bx^2 + cx^3 … + ix^9)/k

to series of doubled numbers up to 1,2,3,4,5,6,7,8,9,10 and here are the results:

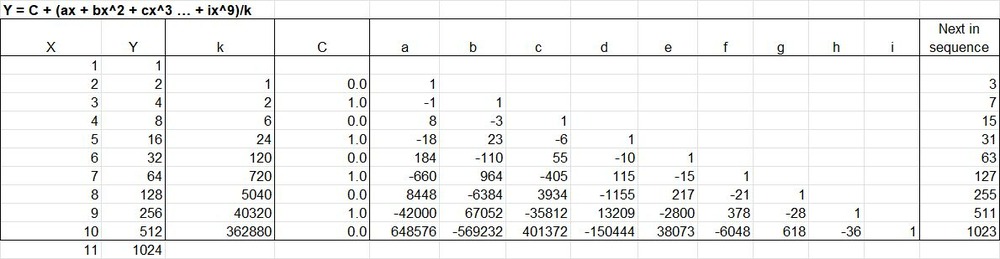
So for any sequence of length n, with a polynomial of order n-1:
The next number in the sequence is always 2^n-1
If the k factor is (n-1)!, the highest power factor is always 1.
The constant C alternates between 1.0 and 0.0
With k=(n-1)! all the other factors are always integers with probably quite simple relationships which I haven’t worked out yet.

The Rev Dodgson said:

I have now fitted polynomials of the form:
Y = C + (ax + bx^2 + cx^3 … + ix^9)/k

to series of doubled numbers up to 1,2,3,4,5,6,7,8,9,10 and here are the results:

So for any sequence of length n, with a polynomial of order n-1:
The next number in the sequence is always 2^n-1
If the k factor is (n-1)!, the highest power factor is always 1.
The constant C alternates between 1.0 and 0.0
With k=(n-1)! all the other factors are always integers with probably quite simple relationships which I haven’t worked out yet.

That’s quite interesting. Thanks.

You probably should’ve used “a” as the highest degree coefficient rather than the lowest. One thing I noticed is that there is a pattern going from a3 to b4 to c5 etc. That is, b4–a3=–2, c5–b4=–3, d6–c5=–4, e7–d6=–5, f8–e7=–6, g9–f8=–7, h10–g9=–8.

The Rev Dodgson said:

mollwollfumble said:

There’s a very easy way to continue the sequence
1,2,4,8,16,31…
It’s called “divided differences”
Take the difference between each pair of numbers, and repeat.

1,2,4,8,16,31
1,2,4,8,15
1,2,4,7
1,2,3

Then extend the sequence and reverse the process.

1,2,3,4,5,6,…
1,2,4,7,11,16,22,…
1,2,4,8,15,26,42,64,…
1,2,4,8,16,31,57,99,163,…

Back in the dim distant past I found it very useful in answering certain questions in IQ tests.

I have now fitted polynomials of the form:
Y = C + (ax + bx^2 + cx^3 … + ix^9)/k

to series of doubled numbers up to 1,2,3,4,5,6,7,8,9,10 and here are the results:

So for any sequence of length n, with a polynomial of order n-1:
The next number in the sequence is always 2^n-1
If the k factor is (n-1)!, the highest power factor is always 1.
The constant C alternates between 1.0 and 0.0
With k=(n-1)! all the other factors are always integers with probably quite simple relationships which I haven’t worked out yet.

like we get that it’s entertaining to play but if the purpose is to confirm that the next number in the sequence is always that next number then why not just do it mollwollfumble’s way extended

as we all know the differences along a finite sequence of powers of 2 are … just powers of 2, that’s how they double, by adding themselves

which means if we take sequences starting from 1, the differences will be sequences starting from 1, again, that’s how it works

which means if we have a polynomial fitted to such a sequence, at the final stage the constant divided difference will be 1

which means if we extend the polynomial fit by an additional term, we repeat the constant divided difference of 1

which means if the sequence was actually powers of 2, then the corresponding divided difference would be 2 instead of 1

which means if we reverse the differencing by adding the 1 instead of the 2, every last difference in the sequence will be 1 less than the actual powers of 2

————

that is

you will notice that for powers of 2 sequences starting from 1, each successive length of sequence is just the previous sequence, added to itself as differences

videre licet

1
+ 1
1   2
+ 1 + 2 
1   2   4
+ 1 + 2 + 4
1   2   4   8
et cetera

so if we instead want powers of 2 sequences starting from 1 but extended by 1 term of polynomial fit, each successive length of sequence is just the previous sequence, added to itself as differences, extended by a term which is deficient by 1

videre licet

1   1
+ 1 + 1
1   2   3
+ 1 + 2 + 3
1   2   4   7
+ 1 + 2 + 4 + 7
1   2   4   8   15
et cetera

nothing special, just a natural consequence

I have worked out an expression for ƒ_n(x), the n-th degree polynomial satisfying ƒ_n(1)=1, ƒ_n(2)=2, ƒ_n(3)=4, ƒ_n(4)=8, … , ƒ_n(n+1)=2ⁿ. Assuming the hypothesis, ƒ_n(n+2)=2ⁿ⁺¹–1 is true for all n:

ƒ_n(x) = 1 + (x+1) + ¹/₂(x+1)(x+2) + ¹/₆(x+1)(x+2)(x+3) + … + ¹/_n!(x+1)(x+2)…(x+n–1)(x+n)

Note that ¹/_n!(x+1)(x+2)…(x+n–1)(x+n) = 0 for x = 1, 2, … , n–1, n, and therefore this term adds 0 to ƒ_n–1(x) at these values of x. The factor of ¹/_n! is necessary to add 1 to 2ⁿ–1 (the hypothesis) to produce 2ⁿ.

CORRECTION:

I have worked out an expression for ƒ_n(x), the n-th degree polynomial satisfying ƒ_n(1)=1, ƒ_n(2)=2, ƒ_n(3)=4, ƒ_n(4)=8, … , ƒ_n(n+1)=2ⁿ. Assuming the hypothesis, ƒ_n(n+2)=2ⁿ⁺¹–1 is true for all n:

ƒ_n(x) = 1 + (x–1) + ¹/₂(x–1)(x–2) + ¹/₆(x–1)(x–2)(x–3) + … + ¹/_n!(x–1)(x–2)…(x–(n–1))(x–n)

Note that ¹/_n!(x–1)(x–2)…(x–(n–1))(x–n) = 0 for x = 1, 2, … , n–1, n, and therefore this term adds 0 to ƒ_n–1(x) at these values of x. The factor of ¹/_n! is necessary to add 1 to 2ⁿ–1 (the hypothesis) to produce 2ⁿ.

Thanks for that KJW.

Just to keep you busy, perhaps you’d like to have a look at the same procedure applied to the sequence 3^(n-1):

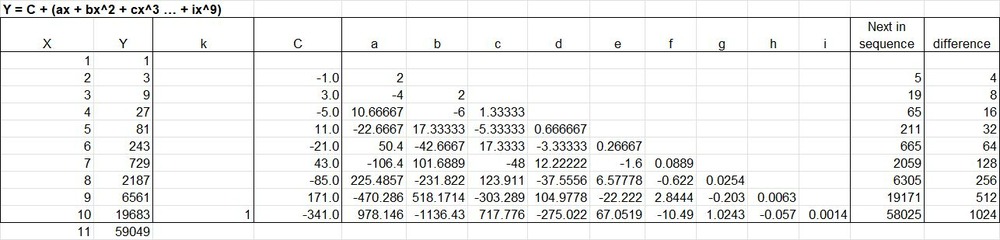
In this case the polynomial projection gives a result that is 2^n less than the next in the 3^(n-1) sequence.

so yous all don’t like the divided differences methods then

SCIENCE said:

so yous all don’t like the divided differences methods then

Meant to thank you for your post too. :)

I confess I found it pretty hard to follow, but I’ll have another look.

The Rev Dodgson said:

SCIENCE said:

so yous all don’t like the divided differences methods then

Meant to thank you for your post too. :)

I confess I found it pretty hard to follow, but I’ll have another look.

thanks well, constructive criticism is like constructive proof, hard truth

see if we can rephrase

SCIENCE said:

like we get that it’s entertaining to play but if the purpose is to confirm that the next number in the sequence is always that next number then why not just do it mollwollfumble’s way extended

as we all know the differences along a finite sequence of powers of 2 are … just powers of 2, that’s how they double, by adding themselves

which means if we take sequences starting from 1, the differences will be sequences starting from 1, again, that’s how it works

which means if we have a polynomial fitted to such a sequence, at the final stage the constant divided difference will be 1

which means if we extend the polynomial fit by an additional term, we repeat the constant divided difference of 1

which means if the sequence was actually powers of 2, then the corresponding divided difference would be 2 instead of 1

which means if we reverse the differencing by adding the 1 instead of the 2, every last difference in the sequence will be 1 less than the actual powers of 2

————

that is

you will notice that for powers of 2 sequences starting from 1, each successive length of sequence is just the previous sequence, added to itself as differences

videre licet

1
+ 1
1   2
+ 1 + 2 
1   2   4
+ 1 + 2 + 4
1   2   4   8
et cetera

so if we instead want powers of 2 sequences starting from 1 but extended by 1 term of polynomial fit, each successive length of sequence is just the previous sequence, added to itself as differences, extended by a term which is deficient by 1

videre licet

1   1
+ 1 + 1
1   2   3
+ 1 + 2 + 3
1   2   4   7
+ 1 + 2 + 4 + 7
1   2   4   8   15
et cetera

nothing special, just a natural consequence

So you want the next number in the sequence, you take the divided differences down to a constant.

In this case, being a finite length sequence of powers of 2, that has to be a single term.

If the first term is 1, then that single term will be 1.

Note that the divided differences along a sequence of powers of 2, are just themselves powers of 2.

1     2     4     8    16    32    64  128
   1     2     4     8    16    32    64
      1     2     4     8    16    32
         1     2     4     8    16
            1     2     4     8
               1     2     4
                  1     2
                     1

Anyway, in this case, to extend the sequence, you have to repeat the constant divided difference and sum back up.

That means instead of

1
+ 1
1   2
+ 1 + 2 
1   2   4
+ 1 + 2 + 4
1   2   4   8
et cetera

so if we instead want powers of 2 sequences starting from 1 but extended by 1 term of polynomial fit, each successive length of sequence is just the previous sequence, added to itself as differences, extended by a term which is deficient by 1

you get

1   1
+ 1 + 1
1   2   3
+ 1 + 2 + 3
1   2   4   7
+ 1 + 2 + 4 + 7
1   2   4   8   15
et cetera

and the 2^n – 1 follows.

Thanks for that; I’ll have a proper look later.

Does the same procedure work for the 3^(n-1) sequence?

Thanks for that; I’ll have a proper look later.

Does the same procedure work for the 3^(n-1) sequence?

The Rev Dodgson said:

Thanks for that; I’ll have a proper look later.

Does the same procedure work for the 3^(n-1) sequence?

d’n‘o’, we didn’t go that far

The Rev Dodgson said:

Thanks for that KJW.

Just to keep you busy, perhaps you’d like to have a look at the same procedure applied to the sequence 3^(n-1):

Actually, I still have to prove the hypothesis for the 2ⁿ case. But the expression I provided does seem ripe for a proof.

But I think I can provide the following generalisation:

Let ƒ_n(x) be an n-th degree polynomial satisfying the following:

For all j > n, and k = 1, 2, …, n, n+1:

ƒ_j(k) = ƒ_n(k)

Then:

ƒ_n(x) = c₀ + c₁(x–1) + c₂(x–1)(x–2) + … + c_n(x–1)(x–2)…(x–n)

for constants c₀, c₁, c₂, …, c_n to be determined. However, it is not clear if these constants depend on n.

KJW said:

However, it is not clear if these constants depend on n.

On further consideration, I believe that the constants are independent of n.

KJW said:

KJW said:

However, it is not clear if these constants depend on n.

On further consideration, I believe that the constants are independent of n.

elucidate

LOL

Just to clarify, c₀, c₁, c₂, etc are all different in general. But the thought occurred to me that maybe c₀, c₁, c₂, etc for f_m are different to c₀, c₁, c₂, etc for f_n. But then I realised this was not the case because c_k determines ƒ_j(k+1) for all j > k, and because ƒ_j(k+1) is the same for all j > k, so must c_k be the same for all j > k.

KJW said:

The Rev Dodgson said:

Thanks for that KJW.

Just to keep you busy, perhaps you’d like to have a look at the same procedure applied to the sequence 3^(n-1):

Actually, I still have to prove the hypothesis for the 2ⁿ case. But the expression I provided does seem ripe for a proof.

But I think I can provide the following generalisation:

Let ƒ_n(x) be an n-th degree polynomial satisfying the following:

For all j > n, and k = 1, 2, …, n, n+1:

ƒ_j(k) = ƒ_n(k)

Then:

ƒ_n(x) = c₀ + c₁(x–1) + c₂(x–1)(x–2) + … + c_n(x–1)(x–2)…(x–n)

for constants c₀, c₁, c₂, …, c_n to be determined. However, it is not clear if these constants depend on n.

Let ƒ_n(k) = 3^k–1 for k = 1, 2, 3, …, n, n+1

For ƒ_n(x) = c₀ + c₁(x–1) + c₂(x–1)(x–2) + … + c_n(x–1)(x–2)…(x–n):

ƒ_n(1) = c₀ = 1
ƒ_n(2) = c₀ + c₁ = 1 + c₁ = 3; c₁ = 2
ƒ_n(3) = c₀ + 2c₁ + 2c₂ = 5 + 2c₂ = 9; c₂ = 2
ƒ_n(4) = c₀ + 3c₁ + 6c₂ + 6c₃ = 19 + 6c₃ = 27; c₃ = ⁴/₃

From here on will probably benefit from the power of Excel.

another find the next term puzzle for yous

SCIENCE said:

another find the next term puzzle for yous

A confounding factor might be that the general rate of childhood death has increased in the UK, due to defunding and mismanagement of the NHS and lower access to food and heating.