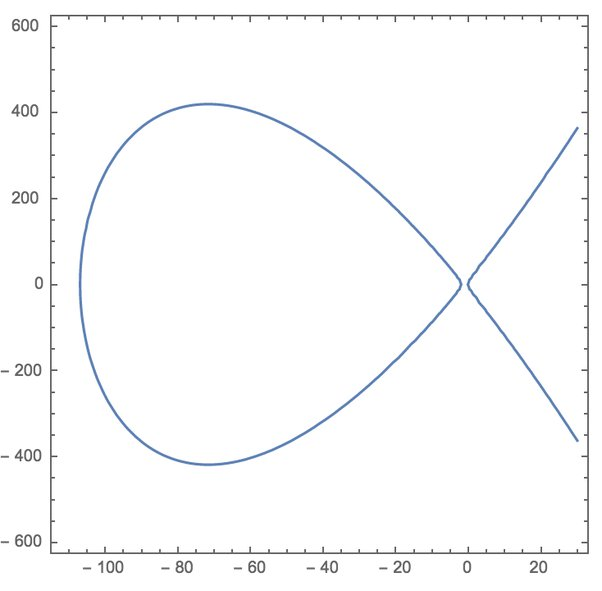
I thought I’d try ChatGPT with that problem.
(Apologies for the poor formatting)
It didn’t go as well as I’d hoped ->
Me: I’d like some help with a mathematical problem please.
GPT: Sure, I’d be happy to help you with a mathematical problem! What’s the problem you’re working on?
Me: What 3 positive integers satisfy the equation: a/(b+c) + b/(a+c) + c/(a+b) = 4
GPT: We can begin by simplifying the left-hand side of the equation and manipulating it algebraically.
a/(b+c) + b/(a+c) + c/(a+b)
= (a^2 + ab + ac + b^2 + bc + ac + ab + bc)/(a+b)(b+c)(a+c)
= (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/(a+b)(b+c)(a+c)
Now we can use the fact that the equation equals 4 to write:
(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/(a+b)(b+c)(a+c) = 4
Multiplying both sides by (a+b)(b+c)(a+c), we get:
(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc) = 4(a+b)(b+c)(a+c)
Expanding the right-hand side, we get:
4(a+b)(b+c)(a+c) = 4a^2b + 4ab^2 + 4a^2c + 8abc + 4b^2c + 4ac^2 + 4bc^2 + 4abc
Simplifying this expression, we get:
4(a+b)(b+c)(a+c) = 4(a+b+c)(ab+ac+bc)
Dividing both sides by 4 and canceling (a+b+c) from both sides, we get:
(a+b)(b+c)(a+c) = (ab+ac+bc)
Now, let’s look at the equation more carefully. We see that the left-hand side is the product of three factors, each of which must be a factor of (ab+ac+bc). In other words, we can write:
a+b = k(ab+ac+bc)
b+c = l(ab+ac+bc)
a+c = m(ab+ac+bc)
where k, l, and m are positive integers.
Multiplying these equations together, we get:
(a+b)(b+c)(a+c) = klm(ab+ac+bc)^3
Substituting the equation we derived earlier, we can rewrite this as:
(ab+ac+bc) = klm(ab+ac+bc)^3
If ab+ac+bc is not equal to 0 or 1, we can simplify this expression to:
1 = klm(ab+ac+bc)^2
Since k, l, m, a, b, and c are positive integers, the only solution to this equation is ab+ac+bc = 1.
Substituting this value into the equation we derived earlier, we get:
(a+b)(b+c)(a+c) = 1
Since a, b, and c are positive integers, the only way this equation can be satisfied is if a = b = c = 1.
Therefore, the solution to the equation a/(b+c) + b/(a+c) + c/(a+b) = 4 is a = b = c = 1.
Me: Thanks, but it isn’t correct. Your solution would be 1/2 + 1/2 + 1/2 = 4
GPT: I apologize for my mistake. Let me try to solve the problem again.
First, we can simplify the expression on the left-hand side by finding a common denominator:
a/(b+c) + b/(a+c) + c/(a+b) = (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/(a+b)(b+c)(a+c)
Now, let’s try to simplify this expression further. We know that a, b, and c are positive integers, so we can assume that a <= b <= c.
Therefore, we have:
a^2 + b^2 + c^2 >= 3a^2
2ab + 2ac + 2bc >= 6ab
Putting these together, we get:
(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/(a+b)(b+c)(a+c) >= (3a^2 + 6ab)/(a+b)(b+c)(a+c)
= 3a/(a+c) + 6b/(a+b)(b+c)
We want to find three positive integers a, b, and c such that the expression above is equal to 4. So we have:
3a/(a+c) + 6b/(a+b)(b+c) = 4
Multiplying both sides by (a+c)(a+b)(b+c), we get:
3a(a+b)(b+c) + 6b(a+c)(b+c) = 4(a+b)(b+c)(a+c)
Expanding both sides, we get:
3a^2b + 3ab^2 + 6abc + 3a^2c + 6abc + 3b^2c = 4a^2b + 4ab^2 + 4abc + 4a^2c + 4b^2c + 4abc
Simplifying, we get:
a^2b + ab^2 + a^2c + 2abc + b^2c = 0
Since a, b, and c are positive integers, this equation can only be true if one of the variables is equal to zero. However, that would mean that the left-hand side of the original equation is undefined, so there are no solutions to the equation.
I thanked it and left that chat.
I’m pretty sure it made a mistake there somewhere.