mollwollfumble said:
The Rev Dodgson said:
mollwollfumble said:
Here it is. The computer program is http://freepages.misc.rootsweb.com/~hallsofjamaica/intgcosf.f
The users guide is http://freepages.misc.rootsweb.com/~hallsofjamaica/Intgcosf.pdf
Thanks for that. Downloaded with no problem.
I’m a bit busy at the moment, but I’ll post in this thread when I have had a look.
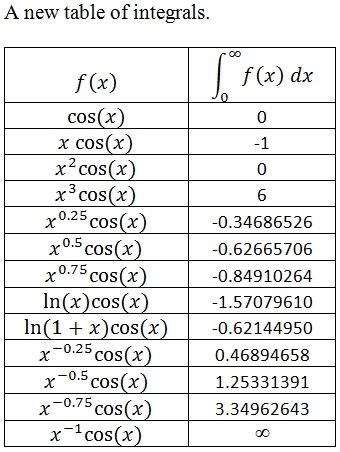
A table of integrals from intgcosf(), with help for the near-zero component out to pi from a calculator on the web.
I have now compiled the Fortran code to run under Python, using F2Py, and also converted it to VBA to run from Excel. For F2Py:
- I converted the file name extension to f90, which removes the line length limit.
- As a result I had to convert the comment marker from ‘c’ to ‘!”. I also converted the variable c to !, which was not a good idea.
- I updated the Gauss integration coefficients to double precision
- I added real*8 before function names, and also replaced dimension statements with real*8 (not sure if that was essential or not)
After a fair bit of fiddling around I got it to compile, and it works from Python, but I haven’t linked that to Excel yet.
For playing with different integration functions I thought it would be easier to convert the whole thing to VBA, which actually wasn’t too hard (a lot quicker than getting it to compile).
Having done that, there are a couple of issues:
- Where x has a negative exponent the calculated integral is too small, because the integration from 0 to Pi is done in a single step, so the approximation of the infinity at x=0 is pretty crude.
- Where x has a positive exponent (especially for x^3) the result changes depending on the value of nint. I actually don’t understand how these functions can have a finite integral when they diverge as x increases, but presumably the mathematicians do.
Did you have a look at the double-exponential oscillating function integrators in the Tanh-Sinh workbook. They seem to work pretty well (and match the results in the table). On my blog there is an all VBA version (by Grame Dennes), and an Excel-Python version (by me).
For my code of your functions, I can copy them to Onedrive and give you a link, or if you would prefer e-mail (or somewhere else), let me know.
