Brilliant

¿what is their funding model?

SCIENCE said:

¿what is their funding model?

https://brilliant.org/premium/?elementId=clicked_b2_home_card

Just downloaded a physics puzzle app. Don’t know how good it is yet.

Brain it on is its name.

I also like the flow free set of maze-like puzzles. Get the first and last ones.

mollwollfumble said:

Just downloaded a physics puzzle app. Don’t know how good it is yet.

Brain it on is its name.

I also like the flow free set of maze-like puzzles. Get the first and last ones.

Brain it on seems like a reasonable price anyway.

Does it have ads?

The Rev Dodgson said:

mollwollfumble said:

Just downloaded a physics puzzle app. Don’t know how good it is yet.

Brain it on is its name.

I also like the flow free set of maze-like puzzles. Get the first and last ones.

Brain it on seems like a reasonable price anyway.

Does it have ads?

Yes.

I liked those soccer physics puzzles someone posted years ago on SSSF.

There are five boxes in a row, 1 to 5.
A cat lives in the boxes. During the day it stays in one of the boxes, but each night it shifts, moving to an adjacent box and spending the following day there.

Each day, you’re permitted to look in one of the boxes, in hopes of finding the cat.

What strategy would you use to minimise the maximum number of boxes you need to check? What is that maximum number?

dv said:

There are five boxes in a row, 1 to 5.
A cat lives in the boxes. During the day it stays in one of the boxes, but each night it shifts, moving to an adjacent box and spending the following day there.

Each day, you’re permitted to look in one of the boxes, in hopes of finding the cat.

What strategy would you use to minimise the maximum number of boxes you need to check? What is that maximum number?

OK, after a lengthy discussion with my dog, I think I’ve got this one.

Check box 2 twice.
Then box 4 thrice.
If you still haven’t found it, it’s in box 2.

The Rev Dodgson said:

dv said:

There are five boxes in a row, 1 to 5.
A cat lives in the boxes. During the day it stays in one of the boxes, but each night it shifts, moving to an adjacent box and spending the following day there.

Each day, you’re permitted to look in one of the boxes, in hopes of finding the cat.

What strategy would you use to minimise the maximum number of boxes you need to check? What is that maximum number?

OK, after a lengthy discussion with my dog, I think I’ve got this one.

Check box 2 twice.
Then box 4 thrice.
If you still haven’t found it, it’s in box 2.

So you’re saying you will look in box 2 on your sixth look?

dv said:

The Rev Dodgson said:

dv said:

There are five boxes in a row, 1 to 5.
A cat lives in the boxes. During the day it stays in one of the boxes, but each night it shifts, moving to an adjacent box and spending the following day there.

Each day, you’re permitted to look in one of the boxes, in hopes of finding the cat.

What strategy would you use to minimise the maximum number of boxes you need to check? What is that maximum number?

OK, after a lengthy discussion with my dog, I think I’ve got this one.

Check box 2 twice.
Then box 4 thrice.
If you still haven’t found it, it’s in box 2.

So you’re saying you will look in box 2 on your sixth look?

That is what I was thinking, but that won’t work so on my 6th go I’ll look in 3, then 2.

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

OK, after a lengthy discussion with my dog, I think I’ve got this one.

Check box 2 twice.
Then box 4 thrice.
If you still haven’t found it, it’s in box 2.

So you’re saying you will look in box 2 on your sixth look?

That is what I was thinking, but that won’t work so on my 6th go I’ll look in 3, then 2.

So that’s 7 looks.

I can tell you that there are various methods of getting it done in 6 looks.

dv said:

The Rev Dodgson said:

dv said:

So you’re saying you will look in box 2 on your sixth look?

That is what I was thinking, but that won’t work so on my 6th go I’ll look in 3, then 2.

So that’s 7 looks.

I can tell you that there are various methods of getting it done in 6 looks.

Oh well.

7 is good enough for an engineer.

(but I’ll probably ask the dog tomorrow anyway)

The Rev Dodgson said:

dv said:

The Rev Dodgson said:

That is what I was thinking, but that won’t work so on my 6th go I’ll look in 3, then 2.

So that’s 7 looks.

I can tell you that there are various methods of getting it done in 6 looks.

Oh well.

7 is good enough for an engineer.

(but I’ll probably ask the dog tomorrow anyway)

check boxes in this order … 2,3,4,4,3,2.

I would check for the warmest box on the first day and get it in one go though.

esselte said:

The Rev Dodgson said:

dv said:

So that’s 7 looks.

I can tell you that there are various methods of getting it done in 6 looks.

Oh well.

7 is good enough for an engineer.

(but I’ll probably ask the dog tomorrow anyway)

check boxes in this order … 2,3,4,4,3,2.

I would check for the warmest box on the first day and get it in one go though.

Esselte gets the prize.

Though there are plenty of other patterns that git er done.

what’s the general solution

SCIENCE said:

what’s the general solution

IDK

I mean for 2 or 3 boxes you can just look twice in #2.
For 4 boxes you can go 2332.
S perhaps a successful strategy for n boxes is to go from 2 to n-1 then n-1 to 2, but I have not checked that that is generally the fastest way.

dv said:

SCIENCE said:

what’s the general solution

IDK

I mean for 2 or 3 boxes you can just look twice in #2.
For 4 boxes you can go 2332.
S perhaps a successful strategy for n boxes is to go from 2 to n-1 then n-1 to 2, but I have not checked that that is generally the fastest way.

It’s a kind-of parity problem. The cat moves, day to day, from and odd numbered box to even numbered, to odd, to even etc. A systematic search requires you to do the same.

So on day one, you start with box 2, an even number. Assuming the cat is in parity, it must be in the only other even numbered box, box 4 on the first day. It can move on the second day to an odd numbered box only (ie 3 or 5) so you check 3. If it is not in three, and the cat and you did start in parity you now know for sure the cat is in box 5 on day 2. and must move to box 4 the following day. So the following day you check box 4. If the cat is not there, it means that you and the cat started out of parity on day one (ie the cat started day one in an odd numbered box), and as long as you are checking odd numbered boxes on days the cat is in an even numbered box (or vice versa) you will obviously never find the cat. So if, after three moves you have not found the cat you know you did not start in and are currently not in parity with the cat then you have to force that parity by breaking your own odd-even alternating pattern. So you choose the even numbered box 4 again on day 4, just as you did on day 3, now knowing that the cat is moving from on odd numbered box on day three to an even numbered box. On day 4, if the cat is not in box 4 you know for sure it is in box 2, and must move either to box one or box 3 on the 5th day. So you check box 3 on the 5th day and the cat is not there, you know for sure it is in box 1 and has to move to box 2 on the sixth day. So on the sixth day you check box 2 and find the cat.

esselte said:

It’s a kind-of parity problem. The cat moves, day to day, from and odd numbered box to even numbered, to odd, to even etc. A systematic search requires you to do the same.

So on day one, you start with box 2, an even number. Assuming the cat is in parity, it must be in the only other even numbered box, box 4 on the first day. It can move on the second day to an odd numbered box only (ie 3 or 5) so you check 3. If it is not in three, and the cat and you did start in parity you now know for sure the cat is in box 5 on day 2. and must move to box 4 the following day. So the following day you check box 4. If the cat is not there, it means that you and the cat started out of parity on day one (ie the cat started day one in an odd numbered box), and as long as you are checking odd numbered boxes on days the cat is in an even numbered box (or vice versa) you will obviously never find the cat. So if, after three moves you have not found the cat you know you did not start in and are currently not in parity with the cat then you have to force that parity by breaking your own odd-even alternating pattern. So you choose the even numbered box 4 again on day 4, just as you did on day 3, now knowing that the cat is moving from on odd numbered box on day three to an even numbered box. On day 4, if the cat is not in box 4 you know for sure it is in box 2, and must move either to box one or box 3 on the 5th day. So you check box 3 on the 5th day and the cat is not there, you know for sure it is in box 1 and has to move to box 2 on the sixth day. So on the sixth day you check box 2 and find the cat.

A simpler way to put this, if on day one the cat and you are both choosing even numbered boxes you will find the cat in 3 days or less. If you have not found the cat in 3 days or less you force the cat in to parity with you and then find the cat in 3 days or less.

esselte said:

dv said:

SCIENCE said:

what’s the general solution

IDK

I mean for 2 or 3 boxes you can just look twice in #2.
For 4 boxes you can go 2332.
S perhaps a successful strategy for n boxes is to go from 2 to n-1 then n-1 to 2, but I have not checked that that is generally the fastest way.

It’s a kind-of parity problem. The cat moves, day to day, from and odd numbered box to even numbered, to odd, to even etc. A systematic search requires you to do the same.

So on day one, you start with box 2, an even number. Assuming the cat is in parity, it must be in the only other even numbered box, box 4 on the first day. It can move on the second day to an odd numbered box only (ie 3 or 5) so you check 3. If it is not in three, and the cat and you did start in parity you now know for sure the cat is in box 5 on day 2. and must move to box 4 the following day. So the following day you check box 4. If the cat is not there, it means that you and the cat started out of parity on day one (ie the cat started day one in an odd numbered box), and as long as you are checking odd numbered boxes on days the cat is in an even numbered box (or vice versa) you will obviously never find the cat. So if, after three moves you have not found the cat you know you did not start in and are currently not in parity with the cat then you have to force that parity by breaking your own odd-even alternating pattern. So you choose the even numbered box 4 again on day 4, just as you did on day 3, now knowing that the cat is moving from on odd numbered box on day three to an even numbered box. On day 4, if the cat is not in box 4 you know for sure it is in box 2, and must move either to box one or box 3 on the 5th day. So you check box 3 on the 5th day and the cat is not there, you know for sure it is in box 1 and has to move to box 2 on the sixth day. So on the sixth day you check box 2 and find the cat.

Thanks esselte.

Your logic on this one was near infinitely better than my approach.

Mr Jones and Mrs Jones, a married couple, attend a party with four other married couples. Some people shake hands, but no one shakes their spouse’s hand, and no one shakes their own hand.

At the end of the party, Mr Jones asks each other person (including his wife) how many people’s hands they shook. Every person gave a different answer. How many people did Mrs Jones shake hands with? How many people did Mr Jones shake hands with?

dv said:

Mr Jones and Mrs Jones, a married couple, attend a party with four other married couples. Some people shake hands, but no one shakes their spouse’s hand, and no one shakes their own hand.

At the end of the party, Mr Jones asks each other person (including his wife) how many people’s hands they shook. Every person gave a different answer. How many people did Mrs Jones shake hands with? How many people did Mr Jones shake hands with?

Somewhere between 0 and 8 for Mrs Jones.
Somewhere between 0 and 8 for Mr Jones.

party_pants said:

dv said:

Mr Jones and Mrs Jones, a married couple, attend a party with four other married couples. Some people shake hands, but no one shakes their spouse’s hand, and no one shakes their own hand.

At the end of the party, Mr Jones asks each other person (including his wife) how many people’s hands they shook. Every person gave a different answer. How many people did Mrs Jones shake hands with? How many people did Mr Jones shake hands with?

Somewhere between 0 and 8 for Mrs Jones.
Somewhere between 0 and 8 for Mr Jones.

party_pants is right, but I’m going to stick my neck out and say 8 for Mrs. J and 0 for Mr. J

The Rev Dodgson said:

party_pants said:

dv said:

Mr Jones and Mrs Jones, a married couple, attend a party with four other married couples. Some people shake hands, but no one shakes their spouse’s hand, and no one shakes their own hand.

At the end of the party, Mr Jones asks each other person (including his wife) how many people’s hands they shook. Every person gave a different answer. How many people did Mrs Jones shake hands with? How many people did Mr Jones shake hands with?

Somewhere between 0 and 8 for Mrs Jones.
Somewhere between 0 and 8 for Mr Jones.

party_pants is right, but I’m going to stick my neck out and say 8 for Mrs. J and 0 for Mr. J

Something doesn’t add up here. There were 10 people at the party, going on the normal definition of married couple. Assuming they shake hands only upon greeting, and they are all there at the same time, given the rule that nobody shakes their own hand or their spouse’s hand: there is a maximum of 8 hand-shakes allowed.

But each of the 10 people report a different answer, when there are only 9 possible answers: 0-8. So there must be some connivance whereby some people shake hands upon leaving, or that some attendees arrive and leave before/after others and they don’t actually meet each other in order to be able to shake hands.

But I won’t be taking the time to work it out.

“But each of the 10 people report a different answer,”

I didn’t say that

party_pants said:

The Rev Dodgson said:

party_pants said:

Somewhere between 0 and 8 for Mrs Jones.
Somewhere between 0 and 8 for Mr Jones.

party_pants is right, but I’m going to stick my neck out and say 8 for Mrs. J and 0 for Mr. J

Something doesn’t add up here. There were 10 people at the party, going on the normal definition of married couple. Assuming they shake hands only upon greeting, and they are all there at the same time, given the rule that nobody shakes their own hand or their spouse’s hand: there is a maximum of 8 hand-shakes allowed.

But each of the 10 people report a different answer, when there are only 9 possible answers: 0-8. So there must be some connivance whereby some people shake hands upon leaving, or that some attendees arrive and leave before/after others and they don’t actually meet each other in order to be able to shake hands.

But I won’t be taking the time to work it out.

I’m pretty sure I got it wrong, but I think the trick is Mr. Jones doesn’t ask himself, so we only need 9 different answers.

The Rev Dodgson said:

party_pants said:

The Rev Dodgson said:

party_pants is right, but I’m going to stick my neck out and say 8 for Mrs. J and 0 for Mr. J

Something doesn’t add up here. There were 10 people at the party, going on the normal definition of married couple. Assuming they shake hands only upon greeting, and they are all there at the same time, given the rule that nobody shakes their own hand or their spouse’s hand: there is a maximum of 8 hand-shakes allowed.

But each of the 10 people report a different answer, when there are only 9 possible answers: 0-8. So there must be some connivance whereby some people shake hands upon leaving, or that some attendees arrive and leave before/after others and they don’t actually meet each other in order to be able to shake hands.

But I won’t be taking the time to work it out.

I’m pretty sure I got it wrong, but I think the trick is Mr. Jones doesn’t ask himself, so we only need 9 different answers.

OK. I’ll pay that.

party_pants said:

The Rev Dodgson said:

party_pants said:

Something doesn’t add up here. There were 10 people at the party, going on the normal definition of married couple. Assuming they shake hands only upon greeting, and they are all there at the same time, given the rule that nobody shakes their own hand or their spouse’s hand: there is a maximum of 8 hand-shakes allowed.

But each of the 10 people report a different answer, when there are only 9 possible answers: 0-8. So there must be some connivance whereby some people shake hands upon leaving, or that some attendees arrive and leave before/after others and they don’t actually meet each other in order to be able to shake hands.

But I won’t be taking the time to work it out.

I’m pretty sure I got it wrong, but I think the trick is Mr. Jones doesn’t ask himself, so we only need 9 different answers.

OK. I’ll pay that.

I’ve been puzzling over this for the last 9 1/2 hours and I still can’t get it to work.

I officially give up.

The Rev Dodgson said:

party_pants said:

The Rev Dodgson said:

I’m pretty sure I got it wrong, but I think the trick is Mr. Jones doesn’t ask himself, so we only need 9 different answers.

OK. I’ll pay that.

I’ve been puzzling over this for the last 9 1/2 hours and I still can’t get it to work.

I officially give up.

And to think it could have come to you in a dream if you’d done the sensible thing and slept last night.

Witty Rejoinder said:

The Rev Dodgson said:

party_pants said:

OK. I’ll pay that.

I’ve been puzzling over this for the last 9 1/2 hours and I still can’t get it to work.

I officially give up.

And to think it could have come to you in a dream if you’d done the sensible thing and slept last night.

I did try that approach too.

7 1/2 hours of sleep wrestling with this problem, and still nothing.

The Rev Dodgson said:

Witty Rejoinder said:

The Rev Dodgson said:

I’ve been puzzling over this for the last 9 1/2 hours and I still can’t get it to work.

I officially give up.

And to think it could have come to you in a dream if you’d done the sensible thing and slept last night.

I did try that approach too.

7 1/2 hours of sleep wrestling with this problem, and still nothing.

Can’t be too logical then.

roughbarked said:

The Rev Dodgson said:

Witty Rejoinder said:

And to think it could have come to you in a dream if you’d done the sensible thing and slept last night.

I did try that approach too.

7 1/2 hours of sleep wrestling with this problem, and still nothing.

Can’t be too logical then.

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

I did try that approach too.

7 1/2 hours of sleep wrestling with this problem, and still nothing.

Can’t be too logical then.

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

Oh well, it is only a puzzle. It is not like you designed Westgate Bridge.

roughbarked said:

The Rev Dodgson said:

roughbarked said:

Can’t be too logical then.

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

Oh well, it is only a puzzle. It is not like you designed Westgate Bridge.

True.

My first job after uni was with the company that designed the Westgate Bridge. I never met the guy who designed it, but did meet people who knew him well, who said he was never the same after the collapse.

The people who died in the collapse were never the same either.

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

Oh well, it is only a puzzle. It is not like you designed Westgate Bridge.

True.

My first job after uni was with the company that designed the Westgate Bridge. I never met the guy who designed it, but did meet people who knew him well, who said he was never the same after the collapse.

The people who died in the collapse were never the same either.

Sorry I picked that example if it still gives you pain.

roughbarked said:

The Rev Dodgson said:

roughbarked said:

Oh well, it is only a puzzle. It is not like you designed Westgate Bridge.

True.

My first job after uni was with the company that designed the Westgate Bridge. I never met the guy who designed it, but did meet people who knew him well, who said he was never the same after the collapse.

The people who died in the collapse were never the same either.

Sorry I picked that example if it still gives you pain.

No pain, it’s just something to think about when tempted to take shortcuts.

I actually did a presentation about the implications of Westgate (and other similar events) earlier this year.

Does Mr Jones always lie?

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

Oh well, it is only a puzzle. It is not like you designed Westgate Bridge.

True.

My first job after uni was with the company that designed the Westgate Bridge. I never met the guy who designed it, but did meet people who knew him well, who said he was never the same after the collapse.

The people who died in the collapse were never the same either.

My father was working on the bridge and whilst he was safe he was never the same after either.

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

True.

My first job after uni was with the company that designed the Westgate Bridge. I never met the guy who designed it, but did meet people who knew him well, who said he was never the same after the collapse.

The people who died in the collapse were never the same either.

Sorry I picked that example if it still gives you pain.

No pain, it’s just something to think about when tempted to take shortcuts.

I actually did a presentation about the implications of Westgate (and other similar events) earlier this year.

It sure is something to keep in the back of your mind on any such project.

The Rev Dodgson said:

roughbarked said:

The Rev Dodgson said:

I did try that approach too.

7 1/2 hours of sleep wrestling with this problem, and still nothing.

Can’t be too logical then.

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

So when is the one true answer going to be revealed?

The Rev Dodgson said:

The Rev Dodgson said:

roughbarked said:

Can’t be too logical then.

Based on previous experience, the answer is probably both logical and obvious, and I’m going to be bloody pissed off when I see it.

So when is the one true answer going to be revealed?

You don’t want to have another go at dreaming an answer?

I’ll use the terms P0, P1, P2 etc to mean people who shook 0, 1, 2 etc hands. There might (as far as we know at this stage of consideration) be two P0s or two P2s etc (though obv it would have to be an even number).

Consider a person who shook no hands, P0.

Consider all the people other than P0 and P0’s spouse. For all of those people, the maximum number of hands they could shake would be 7: they didn’t shake their spouse’s hand, and they also didn’t shake P0’s hand. So P8 be P0’s spouse.

Among the other 8 people, there’s someone who only shook one hand, P1. We know everyone other than P0 shook P8 hand, so P8 is the person whose hand P1 shook. Now there’s someone who shook 7 hands, the unknown P7. Given that P1 shook only one hand (P8), we know they didn’t shake the hand of the person who shook 7 hands. So P1 did not shake P7’s hand, but we know there’s only one non-spouse that P7 did not handshake (P0), therefore P7 is P1’s spouse.

Using similar logic you can show that a P2 is a P6’s spouse etc and eventually that a P4 is a P4’s spouse and that Mr and Mrs Jones each shook 4 hands.

dv said:

I’ll use the terms P0, P1, P2 etc to mean people who shook 0, 1, 2 etc hands. There might (as far as we know at this stage of consideration) be two P0s or two P2s etc (though obv it would have to be an even number).

Consider a person who shook no hands, P0.

Consider all the people other than P0 and P0’s spouse. For all of those people, the maximum number of hands they could shake would be 7: they didn’t shake their spouse’s hand, and they also didn’t shake P0’s hand. So P8 be P0’s spouse.

Among the other 8 people, there’s someone who only shook one hand, P1. We know everyone other than P0 shook P8 hand, so P8 is the person whose hand P1 shook. Now there’s someone who shook 7 hands, the unknown P7. Given that P1 shook only one hand (P8), we know they didn’t shake the hand of the person who shook 7 hands. So P1 did not shake P7’s hand, but we know there’s only one non-spouse that P7 did not handshake (P0), therefore P7 is P1’s spouse.

Using similar logic you can show that a P2 is a P6’s spouse etc and eventually that a P4 is a P4’s spouse and that Mr and Mrs Jones each shook 4 hands.

I’ll pay that.

dv said:

I’ll use the terms P0, P1, P2 etc to mean people who shook 0, 1, 2 etc hands. There might (as far as we know at this stage of consideration) be two P0s or two P2s etc (though obv it would have to be an even number).

Consider a person who shook no hands, P0.

Consider all the people other than P0 and P0’s spouse. For all of those people, the maximum number of hands they could shake would be 7: they didn’t shake their spouse’s hand, and they also didn’t shake P0’s hand. So P8 be P0’s spouse.

Among the other 8 people, there’s someone who only shook one hand, P1. We know everyone other than P0 shook P8 hand, so P8 is the person whose hand P1 shook. Now there’s someone who shook 7 hands, the unknown P7. Given that P1 shook only one hand (P8), we know they didn’t shake the hand of the person who shook 7 hands. So P1 did not shake P7’s hand, but we know there’s only one non-spouse that P7 did not handshake (P0), therefore P7 is P1’s spouse.

Using similar logic you can show that a P2 is a P6’s spouse etc and eventually that a P4 is a P4’s spouse and that Mr and Mrs Jones each shook 4 hands.

d’oh.

dv said:

I’ll use the terms P0, P1, P2 etc to mean people who shook 0, 1, 2 etc hands. There might (as far as we know at this stage of consideration) be two P0s or two P2s etc (though obv it would have to be an even number).

Consider a person who shook no hands, P0.

Consider all the people other than P0 and P0’s spouse. For all of those people, the maximum number of hands they could shake would be 7: they didn’t shake their spouse’s hand, and they also didn’t shake P0’s hand. So P8 be P0’s spouse.

Among the other 8 people, there’s someone who only shook one hand, P1. We know everyone other than P0 shook P8 hand, so P8 is the person whose hand P1 shook. Now there’s someone who shook 7 hands, the unknown P7. Given that P1 shook only one hand (P8), we know they didn’t shake the hand of the person who shook 7 hands. So P1 did not shake P7’s hand, but we know there’s only one non-spouse that P7 did not handshake (P0), therefore P7 is P1’s spouse.

Using similar logic you can show that a P2 is a P6’s spouse etc and eventually that a P4 is a P4’s spouse and that Mr and Mrs Jones each shook 4 hands.

<

Actually I’ve just thought of a much simpler solution.

We know that the non Mr Jones folks run 0 1 2 3 4 5 6 7 8, and we are going to use some means to find out what Mr Jones’s number is.

But whatever method we use, we can use symmetry to apply the same argument concerning the numbers of people that the players did NOT shake hands with.

The only answer that provides this symmetry for Mr Jones is 4.

There’d be a bit more work in showing that Mrs Jones must also be that 4, I suppose.

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

dv said:

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

Your result is inconsistent with mine, and ignores some facts in evidence.

btm said:

dv said:

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

Your result is inconsistent with mine, and ignores some facts in evidence.

Sam lives at 25. Sally lives at 64 and Sue lives at 34.

sibeen said:

btm said:

dv said:

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

Your result is inconsistent with mine, and ignores some facts in evidence.

Sam lives at 25. Sally lives at 64 and Sue lives at 34.

Correction:

Sam at 27.

btm said:

dv said:

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

Your result is inconsistent with mine, and ignores some facts in evidence.

Okay. Let’s say Sam lives at 2, Sally lives at 64, Sue lives at 8.

Sally asks if the number is a perfect square, he says yes (lying). She asks if its over 50, he says yes (lying… not that the piece does not say whether he tells the truth on the 2nd answer.)

This in Sally’s mind would narrow it down to 64 or 81, but since she lives at 64, she thinks he’s at 81, but he ain’t.

Sue asks whether it’s a perfect cube, he says yes, lying. She asks if it is over 25, he says no, telling the truth.

This for her would narrow it to 1 or 8, but she lives at 8, so she thinks it is 1, but it ain’t.

2 is less than both 8 and 64. 8 and 64 sum to double a square.

And this would work whether he was at any number from 2 to 7. So we do not know where Sam lives.

dv said:

btm said:

dv said:

Sally lives at 64, Sue lives at 8, we don’t know where Sam lives.

Your result is inconsistent with mine, and ignores some facts in evidence.

Okay. Let’s say Sam lives at 2, Sally lives at 64, Sue lives at 8.

Sally asks if the number is a perfect square, he says yes (lying). She asks if its over 50, he says yes (lying… not that the piece does not say whether he tells the truth on the 2nd answer.)

This in Sally’s mind would narrow it down to 64 or 81, but since she lives at 64, she thinks he’s at 81, but he ain’t.

Sue asks whether it’s a perfect cube, he says yes, lying. She asks if it is over 25, he says no, telling the truth.

This for her would narrow it to 1 or 8, but she lives at 8, so she thinks it is 1, but it ain’t.

2 is less than both 8 and 64. 8 and 64 sum to double a square.

And this would work whether he was at any number from 2 to 7. So we do not know where Sam lives.

I see my error in the question; the implication was meant to be that Sam answered Sally’s first question untruthfully, and her second question truthfully. Sorry. Also, the sum of all their house numbers (Sam’s, Sally’s, and Sue’s) is twice a perfect square.

Okay so taking it in both cases that he lies to the first question and definitely tells the truth on the second… I’ll start from scratch.

We know Sally thinks she has enough information. That’s still only compatible with receiving the answers yes and yes. The real answers must be no and yes. So Sam > 50 but not a perfect square, and Sally 64 or 81.

Sue also things she has enough information. In this case however, from her standpoint, Yes Yes and Yes No both narrow it down to exactly two. You and I dear reader know he must have answered Yes to the second question anyway, which in Sally’s mind narrows it down to 27 or 64. So Sally is at 27 or 64. All we know about Sam is that he’s > 50, < 100 and not a perfect square or cube.

Since we know Sam is >50, Sally must be 64, which means Sue is 81. That only leaves Sam 55.

dv said:

Actually I’ve just thought of a much simpler solution.

We know that the non Mr Jones folks run 0 1 2 3 4 5 6 7 8, and we are going to use some means to find out what Mr Jones’s number is.

But whatever method we use, we can use symmetry to apply the same argument concerning the numbers of people that the players did NOT shake hands with.

The only answer that provides this symmetry for Mr Jones is 4.

There’d be a bit more work in showing that Mrs Jones must also be that 4, I suppose.

My failure to see the obvious reason reason that Mr and Mrs J had the same number was why I went d’oh.

There are 9 numbers available for 10 people, so if Mrs J was not the same number as Mr J she would have to be the same as someone else, or some other pair would have to be the same.

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally 81
Sue 27
Sam 20

The Rev Dodgson said:

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally 81
Sue 27
Sam 20

Bugger, Sam has to live at >25 so it must be:

Sally 81
Sue 27
Sam 54

The Rev Dodgson said:

The Rev Dodgson said:

btm said:

Sam, Sally, and Sue all live on the same street, but in different houses. The house numbers on this street are consecutive and go from 1 to 99. Sue and Sally both want to date Sam, but neither knows which house he lives in.

Sally asks him two questions: “Is your house number a perfect square?”, and “Is your house number greater than 50?” Sam answers both questions. Sally thinks she has enough information, and decides to pay him a visit, but finds she’s at the wrong house — hardly surprising, because Sam’s answer to the first question was a lie.

Now Sue, unaware of Sally’s conversation, asks him two questions: “Is your house number a perfect cube?” and “Is your house number greater than 25?” Sam answers both questions. Sue decides that she has enough information, and goes for a visit, finding that she’s wrong — hardly surprising, since Sam only answered Sue’s second question truthfully.

Sam’s house number is less than Sue’s or Sally’s, and the sum of their house numbers is twice a perfect square.

What are their addresses?

Sally 81
Sue 27
Sam 20

Bugger, Sam has to live at >25 so it must be:

Sally 81
Sue 27
Sam 54

Still wrong, Sam has to be less than Sue:
Sally 81
Sue 64
Sam 55

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

Really… all capitals is considered to be shouting on the internet. You should tame it down by using ‘and’ and ‘or’ and people would appreciate it. Just saying.

sibeen said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

Really… all capitals is considered to be shouting on the internet. You should tame it down by using ‘and’ and ‘or’ and people would appreciate it. Just saying.

Sorry. It’s nighttime, too, so people are asleep. How about and and or?

btm said:

sibeen said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

Really… all capitals is considered to be shouting on the internet. You should tame it down by using ‘and’ and ‘or’ and people would appreciate it. Just saying.

Sorry. It’s nighttime, too, so people are asleep. How about and and or?

Better, that way they can xnor :)

sibeen said:

btm said:

sibeen said:

Really… all capitals is considered to be shouting on the internet. You should tame it down by using ‘and’ and ‘or’ and people would appreciate it. Just saying.

Sorry. It’s nighttime, too, so people are asleep. How about and and or?

Better, that way they can xnor :)

:)

btm said:

sibeen said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

Really… all capitals is considered to be shouting on the internet. You should tame it down by using ‘and’ and ‘or’ and people would appreciate it. Just saying.

Sorry. It’s nighttime, too, so people are asleep. How about and and or?

Shouldn’t have shouted, you woke me up.

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

I have no idea what the strange symbols following “provided “ mean, or even what “inverted” means in this context, but I will assume an inverter inverts things and the inputs are invertable so the answer is 1.

The Rev Dodgson said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

I have no idea what the strange symbols following “provided “ mean, or even what “inverted” means in this context, but I will assume an inverter inverts things and the inputs are invertable so the answer is 1.

The stuff after provided: Output 1 is the inverse of input 1, output 2 is the inverse of input 2 etc.

“Inverted” means that the gate takes a True/1/On signal as input and outputs a False/0/Off signal, and vice versa.

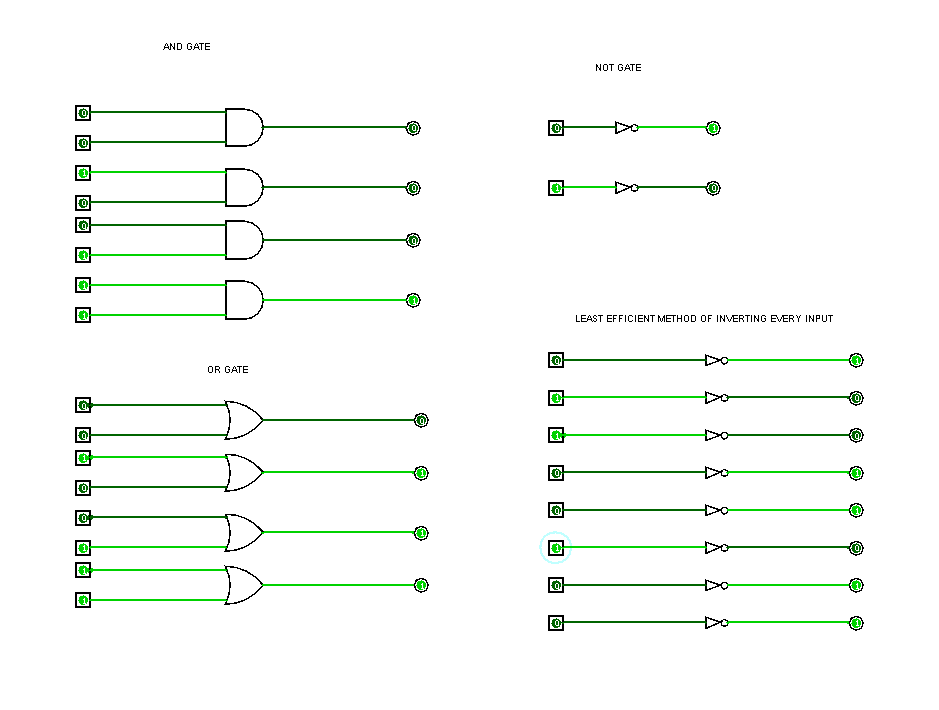
Microcircuits use gates to process electrical signals. The two fundamental gates are the AND gate and the NOT gate. Every possible circuit and every other possible type of gate are built from these two. The Apollo missions to the Moon had computers that were built entirely of NAND gates (a combination of a single AND gate and a single NOT gate) for example. The NOT gate takes a single input signal and inverts it to the output. The AND gate takes two input signals and gives an output based on them (literally “If input A is true AND input B is true, output P will be true”).

An OR gate is built from two NOT gates feeding a signal in to an AND gate and then inverting that result.

esselte said:

The Rev Dodgson said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

I have no idea what the strange symbols following “provided “ mean, or even what “inverted” means in this context, but I will assume an inverter inverts things and the inputs are invertable so the answer is 1.

The stuff after provided: Output 1 is the inverse of input 1, output 2 is the inverse of input 2 etc.

“Inverted” means that the gate takes a True/1/On signal as input and outputs a False/0/Off signal, and vice versa.

Microcircuits use gates to process electrical signals. The two fundamental gates are the AND gate and the NOT gate. Every possible circuit and every other possible type of gate are built from these two. The Apollo missions to the Moon had computers that were built entirely of NAND gates (a combination of a single AND gate and a single NOT gate) for example. The NOT gate takes a single input signal and inverts it to the output. The AND gate takes two input signals and gives an output based on them (literally “If input A is true AND input B is true, output P will be true”).

An OR gate is built from two NOT gates feeding a signal in to an AND gate and then inverting that result.

Thanks esselte.

It still isn’t clear to me why the answer isn’t 1 though.

The diagram below gives all the info required to answer the question I think.

It shows all possible states of AND, OR and NOT gates, as well as the least efficient method of inverting every input.

The question is, by inserting AND and OR gates between the inputs and outputs, what is the least number of NOT gates required to invert every input?

The answer would be at least 2 as you need the ability to compare different inputs in a parallel fashion, but I don’t know at this stage what that circuit would look like or even if it’s possible.

esselte said:

The diagram below gives all the info required to answer the question I think.

It shows all possible states of AND, OR and NOT gates, as well as the least efficient method of inverting every input.

The question is, by inserting AND and OR gates between the inputs and outputs, what is the least number of NOT gates required to invert every input?

The answer would be at least 2 as you need the ability to compare different inputs in a parallel fashion, but I don’t know at this stage what that circuit would look like or even if it’s possible.

Well I’m glad one of us understands btmese. :)

The Rev Dodgson said:

esselte said:

The diagram below gives all the info required to answer the question I think.

It shows all possible states of AND, OR and NOT gates, as well as the least efficient method of inverting every input.

The question is, by inserting AND and OR gates between the inputs and outputs, what is the least number of NOT gates required to invert every input?

The answer would be at least 2 as you need the ability to compare different inputs in a parallel fashion, but I don’t know at this stage what that circuit would look like or even if it’s possible.

Well I’m glad one of us understands btmese. :)

Anyone who likes logic puzzles should download Logisim and learns the basics IMO, and then set themselves tasks as “puzzles” to create circuits that do specific things. Hours of entertainment value plus you get to learn a bit more about how computers work.

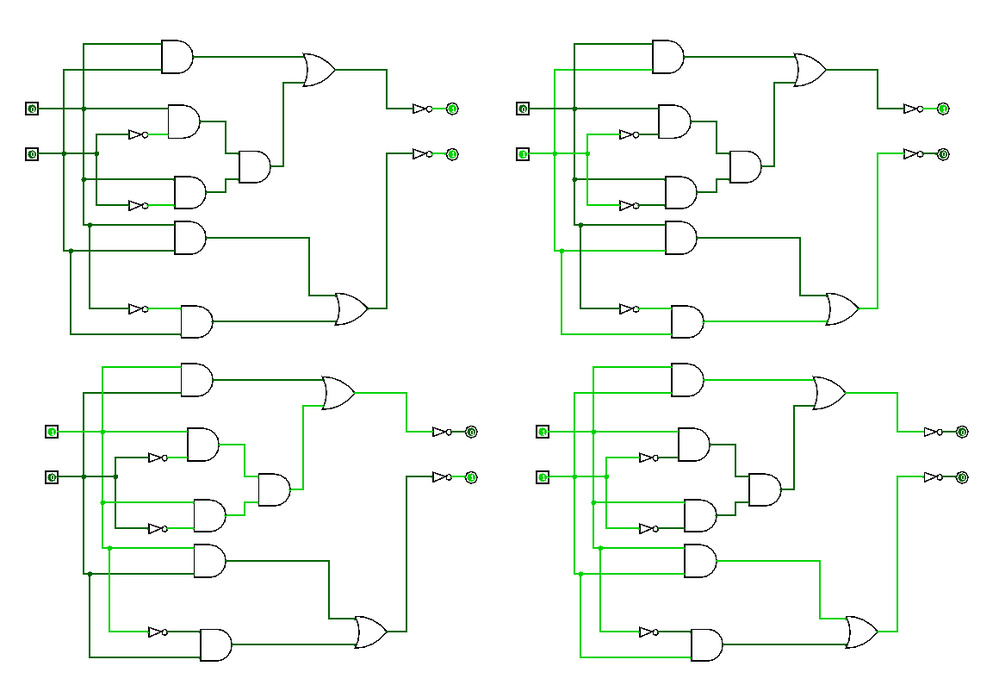
Below is a circuit which will invert 2 inputs, but notably in terms of using the least number of possible NOT gates this is less efficient than simply using a single NOT between each of the inputs and outputs (what I labelled “least efficient” in the previous posts). So whilst this is not the answer and is not even the most efficient method of doing two inputs, it does demonstrate the “kind” of circuits I think we would need to build for unlimited inputs with inverted outputs.

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

esselte had a good shot at it, and was on the right track, but used 5 inverters to invert 2 inputs. Here’s my solution:

Using conventional notation (· for AND, “+” for OR, and overbar (  ) for inversion); · has higher precedence than +:

In the trivial case N = 1, only a single inverter is needed.
Consider the case N=3:

n₁ = (i₁ · i₂) + (i₁ · i₃) + (i₂ · i₃)

n₂ = ((i₁ + i₂ + i₃) · n₁) + (i₁ · (i₂ · i₃)
o₁= ((i₂ + i₃ + n₂) · n₁) + (i₂ · i₃ · n₂)
o₂= ((i₁ + i₃ + n₂) · n₁) + (i₁ · i₃ · n₂)
o₃= ((i₁ + i₂ + n₂) · n₁) + (i₁ · i₂ · n₂)

So only 2 inverters are needed to invert 3 inputs. If N>3 applying the above procedure to each group of 3 inverters reduces the number of inverters needed from N to ⅔N. Keep applying this until only 2 inverters are left. So it’s possible to invert any number (>1) of inputs using no more than 2 inverters (though for large N there’s nontrivial settle time.)

btm said:

btm said:

Consider an electronic logic system with N inputs: i₁, i₂, i₃, i₄ … i_N. Given unlimited AND and OR gates, what is the minimum number of inverters necessary to invert each input, providing o₁ = i₁, o₂ = i₂, o₃ = i₃ … o_N = i_N,

esselte had a good shot at it, and was on the right track, but used 5 inverters to invert 2 inputs. Here’s my solution:

Using conventional notation (· for AND, “+” for OR, and overbar (  ) for inversion); · has higher precedence than +:

In the trivial case N = 1, only a single inverter is needed.
Consider the case N=3:

n₁ = (i₁ · i₂) + (i₁ · i₃) + (i₂ · i₃)

n₂ = ((i₁ + i₂ + i₃) · n₁) + (i₁ · (i₂ · i₃)
o₁= ((i₂ + i₃ + n₂) · n₁) + (i₂ · i₃ · n₂)
o₂= ((i₁ + i₃ + n₂) · n₁) + (i₁ · i₃ · n₂)
o₃= ((i₁ + i₂ + n₂) · n₁) + (i₁ · i₂ · n₂)

So only 2 inverters are needed to invert 3 inputs. If N>3 applying the above procedure to each group of 3 inverters reduces the number of inverters needed from N to ⅔N. Keep applying this until only 2 inverters are left. So it’s possible to invert any number (>1) of inputs using no more than 2 inverters (though for large N there’s nontrivial settle time.)

It’s all Boolean to me.

Prove that any group of six or more people contains three mutual acquaintances or three mutual strangers.

y ^y³ = 729

Find y

dv said:

y ^y³ = 729

Find y

I’m a fair man so I’ll only require to find the real solution

dv said:

dv said:

y ^y³ = 729

Find y

I’m a fair man so I’ll only require to find the real solution

Well, that was fairly easy :)

sibeen said:

dv said:

dv said:

y ^y³ = 729

Find y

I’m a fair man so I’ll only require to find the real solution

Well, that was fairly easy :)

Or 2.08008382325474 to be a little more precise.

The Rev Dodgson said:

sibeen said:

dv said:

I’m a fair man so I’ll only require to find the real solution

Well, that was fairly easy :)

Or 2.08008382325474 to be a little more precise.

And to be a little more accurate:
2.0800838231

The Rev Dodgson said:

The Rev Dodgson said:

sibeen said:

Well, that was fairly easy :)

Or 2.08008382325474 to be a little more precise.

And to be a little more accurate:
2.0800838231

I’ll have a think later. Have to cook tea first – flake + salad.

I bet there’ll be a ‘ln’ in there somewhere, there always is.

The Rev Dodgson said:

The Rev Dodgson said:

sibeen said:

Well, that was fairly easy :)

Or 2.08008382325474 to be a little more precise.

And to be a little more accurate:
2.0800838231

And to be both precise and accurate:
729^(1/9)

sibeen said:

dv said:

dv said:

y ^y³ = 729

Find y

I’m a fair man so I’ll only require to find the real solution

Well, that was fairly easy :)

I still don’t think you are getting the hang of these?

When the ABC Friday Quiz comes out, you can guarantee a 10/10 just by Googling the answers. It will be an unrewarding activity but you can do it. Or you can look up the wordle of the day and be sure to solve them in one guess every time.

If you don’t want to work on solving these, just leave them alone.

The Rev Dodgson said:

The Rev Dodgson said:

The Rev Dodgson said:

Or 2.08008382325474 to be a little more precise.

And to be a little more accurate:
2.0800838231

And to be both precise and accurate:
729^(1/9)

Show working

sibeen said:

The Rev Dodgson said:

The Rev Dodgson said:

Or 2.08008382325474 to be a little more precise.

And to be a little more accurate:
2.0800838231

I’ll have a think later. Have to cook tea first – flake + salad.

I bet there’ll be a ‘ln’ in there somewhere, there always is.

OK – thinking cap on.

Looking at it, the cube root of 729 happens to be 9. So we have:

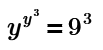
But then by the power of exponents, for the LHS, we have:

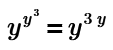
Giving me:

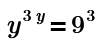
Goes for another beer…

sibeen said:

sibeen said:

The Rev Dodgson said:

And to be a little more accurate:
2.0800838231

I’ll have a think later. Have to cook tea first – flake + salad.

I bet there’ll be a ‘ln’ in there somewhere, there always is.

OK – thinking cap on.

Looking at it, the cube root of 729 happens to be 9. So we have:

But then by the power of exponents, for the LHS, we have:

Giving me:

Goes for another beer…

BTW, the flake was bloody excellent. All the family enjoyed it.

sibeen said:

sibeen said:

sibeen said:

I’ll have a think later. Have to cook tea first – flake + salad.

I bet there’ll be a ‘ln’ in there somewhere, there always is.

OK – thinking cap on.

Looking at it, the cube root of 729 happens to be 9. So we have:

But then by the power of exponents, for the LHS, we have:

Giving me:

Goes for another beer…

BTW, the flake was bloody excellent. All the family enjoyed it.

Jaysus, ignore the above – except for the flake bit.

As Mr Lennon said, I’m starting over…

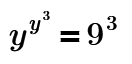
sibeen said:

sibeen said:

sibeen said:

OK – thinking cap on.

Looking at it, the cube root of 729 happens to be 9. So we have:

But then by the power of exponents, for the LHS, we have:

Giving me:

Goes for another beer…

BTW, the flake was bloody excellent. All the family enjoyed it.

Jaysus, ignore the above – except for the flake bit.

Hmmmm minamata disease by the sounds.

JudgeMental said:

sibeen said:

sibeen said:

BTW, the flake was bloody excellent. All the family enjoyed it.

Jaysus, ignore the above – except for the flake bit.

Hmmmm minamata disease by the sounds.

I was doing a brackets in my head that didn’t exist. FIIK why,

OK – cracks knuckles:

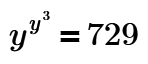
Cube both sidesw:

Now I use the fact that

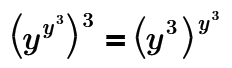
and I get

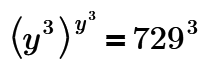
Making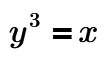

I then have:

which goes down to:

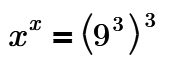
so that x will fucking equal:

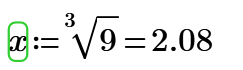
QE fucking D.

goes for beer,,,my brain hurts

And ‘In’ didn’t make an appearance, even though I spent ages trying to shoehorn it in somehow, Bastard.

sibeen said:

OK – cracks knuckles:

Cube both sidesw:

Now I use the fact that

and I get

Making

I then have:

which goes down to:

so that x will fucking equal:

QE fucking D.

goes for beer,,,my brain hurts

I love you, man

Fuck. I was listening to one of my favoutite albums yesterday, Laurie Anderson’s ‘Big Science’. I should have slipped in her

https://www.youtube.com/watch?v=UfOK0evCqZY&ab_channel=LaurieAnderson-Topic

sibeen said:

OK – cracks knuckles:

Cube both sidesw:

Now I use the fact that

and I get

Making

I then have:

which goes down to:

so that x will fucking equal:

QE fucking D.

goes for beer,,,my brain hurts

Re-reading that in the light of day I really should have had the last few lines as:

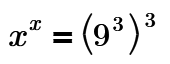
Which I had in and then should have shown the step

and as we have

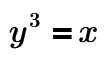
then obviously

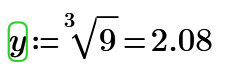
sibeen said:

sibeen said:

OK – cracks knuckles:

Cube both sidesw:

Now I use the fact that

and I get

Making

I then have:

which goes down to:

so that x will fucking equal:

QE fucking D.

goes for beer,,,my brain hurts

Re-reading that in the light of day I really should have had the last few lines as:

Which I had in and then should have shown the step

and as we have

then obviously

I think you’re in some sort of mid-life crisis.

Witty Rejoinder said:

sibeen said:

sibeen said:

OK – cracks knuckles:

Cube both sidesw:

Now I use the fact that

and I get

Making

I then have:

which goes down to:

so that x will fucking equal:

QE fucking D.

goes for beer,,,my brain hurts

Re-reading that in the light of day I really should have had the last few lines as:

Which I had in and then should have shown the step

and as we have

then obviously

I think you’re in some sort of mid-life crisis.

Deevs taunted me and shamed me into doing it.

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

btm said:

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

Presumably with a sharp knife.

btm said:

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

With n-1 equispaced parallel slices.

This was not very difficult.

dv said:

btm said:

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

With n-1 equispaced parallel slices.

This was not very difficult.

Good point. Now consider a different problem in which the cake must be cut into n wedges of equal volume and equal surface area, with the wedges radiating from the centre of the cake.

btm said:

dv said:

btm said:

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

With n-1 equispaced parallel slices.

This was not very difficult.

Good point. Now consider a different problem in which the cake must be cut into n wedges of equal volume and equal surface area, with the wedges radiating from the centre of the cake.

I’ve done one. SCIENCE can handle the next one.

btm said:

dv said:

btm said:

Consider a square cake with side length s and depth d. How can the cake be cut into n pieces of equal volume and equal surface area?

With n-1 equispaced parallel slices.

This was not very difficult.

Good point. Now consider a different problem in which the cake must be cut into n wedges of equal volume and equal surface area, with the wedges radiating from the centre of the cake.

Still a square cake?

Divide into 4 wedges through the middle of each side.
If n > 4 divide each wedge into two equal pieces by dividing through the corners.
If n < 8, throw away the pieces you don’t want.
If n>8 I’m going to say it can’t be done.

The Rev Dodgson said:

btm said:

dv said:

With n-1 equispaced parallel slices.

This was not very difficult.

Good point. Now consider a different problem in which the cake must be cut into n wedges of equal volume and equal surface area, with the wedges radiating from the centre of the cake.

Still a square cake?

Divide into 4 wedges through the middle of each side.
If n > 4 divide each wedge into two equal pieces by dividing through the corners.
If n < 8, throw away the pieces you don’t want.
If n>8 I’m going to say it can’t be done.

Correction:
If n>8 you can divide eqch wedge with horizontal slices of equal area and volume, and they are still wedges, so n can be as large as you like.

dv said:

btm said:

dv said:

With n-1 equispaced parallel slices.

This was not very difficult.

Good point. Now consider a different problem in which the cake must be cut into n wedges of equal volume and equal surface area, with the wedges radiating from the centre of the cake.

I’ve done one. SCIENCE can handle the next one.

computationally