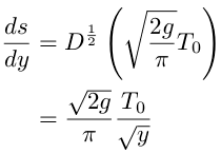The following is worth a read:
https://www.cantorsparadise.com/fractional-calculus-48192f4e9c9f
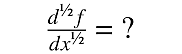
“what it could possibly mean to do something like take a 1/2 order derivative, and so introduce the theory of the fractional calculus.”
The nth order integral is
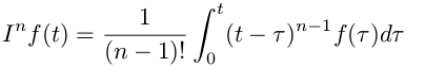
Generalising that to non-integer order
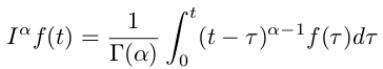
“It’s called the left Riemann-Liouville integral. There are in fact many different fractional integration operators that are accepted in the literature, but the R-L integral is the simplest and easiest to use and understand. Note that α may also be complex with real part strictly greater than zero, for simplicity we will assume that α is real. The special case of α = 1/2 is called the semi-integral.”
We can’t simply get differentiation as the inverse operation of integration. The best we can do is to differentiate an integer number of times and then add a fractional integral to make up the non-integer component.
That gives
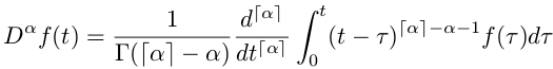
where ⌈⌉ is the “ceiling operator”.
For power functions with n ≥ 0 the fractional differential is given by:

This implies that the fractional derivative of a constant, surprisingly, is not zero. The semi-derivative of f(t)=1, constant, is worth memorising and is given by:
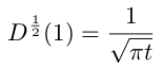
The fractional derivative of sine is

The fractional derivative of the exponential function is
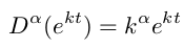
(Note from mollwollfumble, it would be interesting to compare that with what happens when we integrate and differentiate the Taylor series).
A practical application
Neils Abel (1802–1829) is generally credited as being the first mathematician to develop the basic ideas of fractional calculus. The tautochrone problem asks one to construct a curve with the property that when a bead slides down the curve, the time it takes to reach the bottom of the curve is independent of the initial height.

We need to solve this equation for ds/dy.
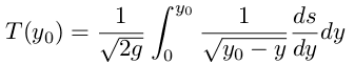
The answer is the cycloid calculated from the semi-deriviative: