dv said:
buffy said:
https://www.scientificamerican.com/article/discovery-of-elusive-einstein-tile-raises-more-questions-than-it-answers/
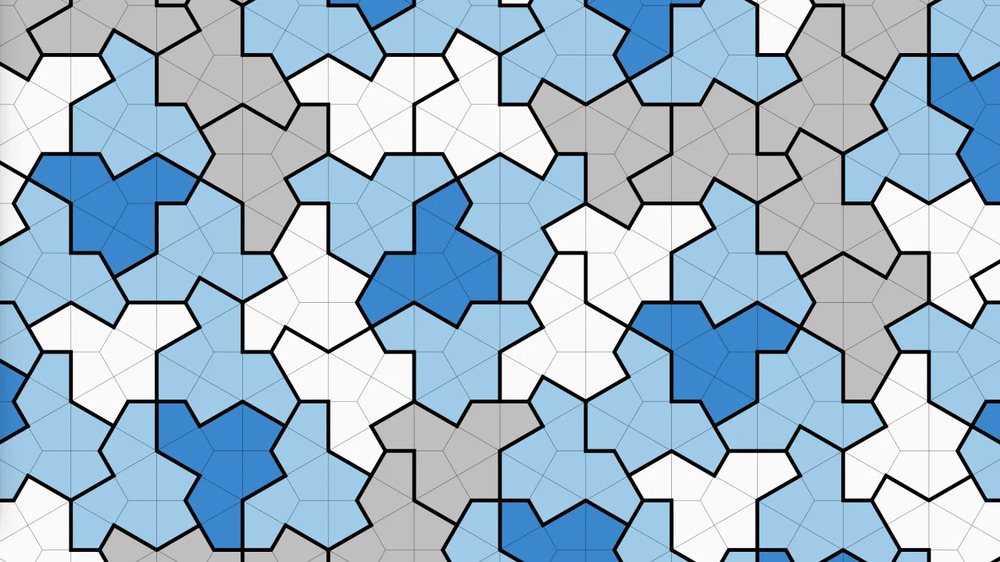
“If you used einstein-shaped tiles to cover your bathroom floor—or any flat surface, even if infinitely large—they would fit together perfectly but never form a repeating pattern.”
It’s interesting that there is an underlying set of hexagons and triangles.
I immediately see a repeated pattern in the example they give. What a weird thing to say.
Didn’t we have this a few weeks (months?) ago?
I must admit, I didn’t see how a pattern with a small number of shapes, orientations and colours could have an infinite number of different arrangements, but I’m afraid I just assumed these maths geniuses understood these things better than I do.